В статье рассмотрена бесступенчатая механическая передача на основе планетарного вариатора в качестве трансформатора крутящего момента трансмиссий специальных колесных шасси и методика определения его основных параметров.
Ключевые слова: трансмиссия, планетарный вариатор, контактные напряжения.
Для повышения эффективности применения специальных колесных шасси наиболее предпочтительным является решение технических проблем, влияющие на ее основные составляющие. К этим составляющим относится показатель живучести с входящими в него характеристиками — это подвижность, защищенность, заметность и коэффициент готовности транспортных средств к маршу.
Составной частью транспортного средства, обеспечивающей его подвижность, является трансмиссия. Каждый тип транспортной или тяговой машины имеет свою специфику, определяемую назначением машины и условиями ее работы [1]. В настоящее время на специальных колесных шасси применяются механическая и гидромеханическая трансмиссии, имеющих как свои достоинства, так и недостатки.
В настоящее время на автомобилях применяются механическая, гидромеханическая, электрическая, гидрообъемная (гидростатическая) трансмиссии. Из них бесступенчатыми являются:
− электрическая;
− гидрообъемная;
− механическая на основе вариатора.
Аналитический обзор существующих бесступенчатых трансмиссий, указывает, что оптимальным выбором является механическая трансмиссия с вариатором.
Механической трансмиссией называется такая, в которой все передающие и преобразующие элементы механические. Достоинства механической бесступенчатой трансмиссии на основе клиноременного вариатора: простота конструкции; бесшумность работы; удобство и простота в управлении; плавность разгона и движения; сравнительно больший КПД (в зависимости от передаточного отношения до 0,95); дешевизна в производстве; более высокая топливная экономичность; щадящий режим работы двигателя.
Однако существующая клиноременная передача имеет существенный недостаток — ограничение передаваемого крутящего момента. Кроме того, возможности существующих и перспективных образцов специальных колесных шасси с механической ступенчатой, либо гидромеханической трансмиссиями, с точки зрения увеличения маневренных возможностей практически исчерпаны.
Данный недостаток представляется возможным устранить применив бесступенчатый механический планетарный вариатор [3]. Принципиальная схема вариатора показана на рис. 1.
Механическая бесступенчатая фрикционная передача выгодно отличаются от гидравлических и электрических передач.
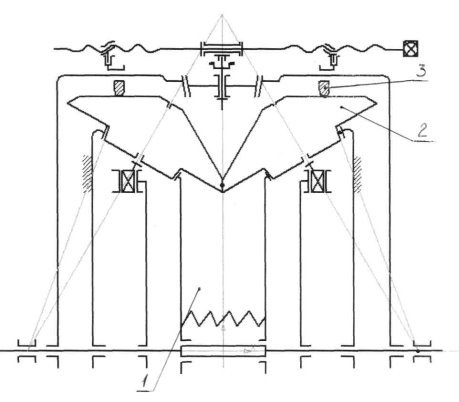
Рис. 1. Принципиальная схема вариатора: 1 — ведущий конус, 2 — сателлит, 3 — ведомое кольцо
Фрикционная бесступенчатая передача имеет следующие главные достоинства в сравнении с другими видами передач:
− простота конструкции тел качения;
− равномерность передачи движения и, как следствие, бесшумность работы, что делает возможным их применение при высоких числах оборотов;
− способность преобразовывать большие крутящие моменты;
− наибольший коэффициент полезного действия в сравнении с другими видами бесступенчатых передач;
− достаточно жесткая характеристика зависимости передаточного отношения от нагрузки;
− сравнительно малый удельный объем передачи.
Однако наряду с достоинствами, передача имеет и недостатки, из которых главные следующие:
− она неприменима там, где не допускается накопление ошибки передаточного отношения;
− в ней возможен неравномерный износ фрикционных тел из-за пробуксовки.
Значение отмеченных выше недостатков, а также и других неуказанных здесь может быть сведено к минимуму путем выбора рациональной схемы бесступенчатой фрикционной передачи и определения ее оптимальных параметров.
Применение данного типа трансмиссии на специальных колесных шасси, по нашему мнению, позволит повысить средние скорости движения, снизит утомляемость механиков-водителей, что в итоге приведет к расширению маневренных возможностей и повышению эффективности их применения.
Однако, в настоящее время отсутствует методика расчета основных параметров данного вариатора применительно к трансмиссиям специальных колесных шасси, имеющих большую массу и значительные крутящие моменты двигателей.
Основными параметрами вариатора, определив которые мы можем вычислить все остальные, являются радиус ведомого кольца R (рис. 2), большой радиус сателлита rB, малый радиус сателлита rА и угол наклона сателлита β.
Чтобы обеспечить передачу заданной мощности, следует исходить из допускаемых контактных напряжений на поверхности основного фрикционного контакта. В передаче (рис. 1) основным фрикционным контактом будет контакт между кольцом 3 и сателлитом 2.
В курсе деталей машин допускаемые контактные напряжения определяют по формуле Герце-Беляева
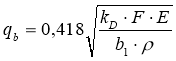 , (1)
, (1)
где F- сила сжатия рассчитываемых фрикционных тел; Е- модуль упругости первого рода материала; 1/ρ — приведенный радиус кривизны контактирующих поверхностей; b1- длина контакта; kD- коэффициент долговечности, который вводится при расчете металлических тел качения и учитывает потребный срок службы передачи и переменность режима работы.
Из формулы (1) определим допустимую силу FД
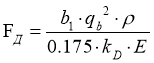 (2)
(2)
или
![]() ,(3)
,(3)
где 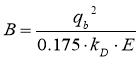 - постоянная величина.
- постоянная величина.
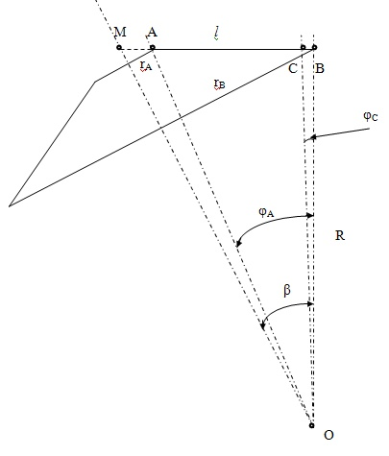
Рис. 2. К определению приведенного радиуса кривизны
Определим приведенный радиус кривизны в месте основного контакта (в точке С, рис. 2).
Радиус кривизны сателлита в плоскости ведомого кольца определяется по формуле
![]() , (4)
, (4)
где li — расстояние от точки М до точки на образующей сателлита; β- угол наклона сателлита.
Из рисунка мы видим, что
lС= МА+l-СВ,(5)
где
МА+ l = R tgβ;(6)
CB= R tgφc.(7)
Найдем угол φС через угол φА:
![]() ; (8)
; (8)
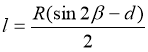 .(9)
.(9)
Подставив выражение (9) в формулу (8), получим
![]() ,(10)
,(10)
где d — отношение радиуса кольца к расстоянию МА.
Передаточное отношение вариатора определяется по формуле
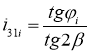 ,(11)
,(11)
где, φi — угол между перпендикуляром ОВ и i- й точкой на образующей l.
Получим
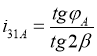 . (12)
. (12)
Диапазон регулирования передаточного отношения определяется по формуле [1]
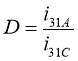 ,(13)
,(13)
откуда получим
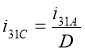 .(14)
.(14)
В свою очередь из формулы (11) для точки С имеем
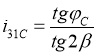 ,(15)
,(15)
откуда
![]() . (16)
. (16)
Подставив выражения (6) и (7) в формулу (5), получим
![]() .(17)
.(17)
Подставив выражения (17) в формулу (4) запишем
![]() . (18)
. (18)
Приведенный радиус кривизны определяется по известной формуле [4]
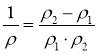 ,(19)
,(19)
где ρ1- ρС, ρ2- R.
После преобразований
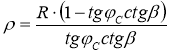 (20)
(20)
С учетом формулы (20) и b= b1/R выражение (3) будет иметь вид:
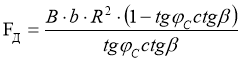 .(21)
.(21)
Потребную силу FП в точке С определим из условия равенства мощностей на ведущем и ведомом валах
![]() , (22)
, (22)
где М1 и n1 — крутящий момент и частота вращения входного вала; М3С и n3 — крутящий момент и частота вращения выходного вала ηп — коэффициент полезного действия передачи, который в первом приближении считаем ηп=1.
Из данного выражения получим
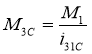 , (23)
, (23)
где i31C — передаточное отношение передачи, когда кольцо находится в точке С.
С другой стороны, реактивный момент в точке С определяют
![]() , (24)
, (24)
где i- число сателлитов одного ряда; f- коэффициент трения с учетом коэффициента запаса сцепления.
Приравняв выражения (23) и (24), получим
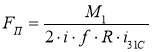 .(25)
.(25)
Потребная сила FП должна быть равной допустимой силе FД, поэтому приравнивая их запишем
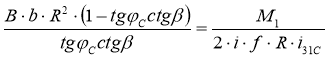 .
.
Откуда выведем радиус ведомого кольца
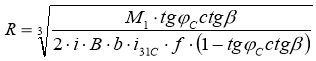 .(26)
.(26)
Используя выражение (26) определяют остальные основные геометрические пара параметры передачи, являются основой при разработке конструкторско-технической документации для изготовления передачи.
В предложенной методике расчета основных параметров учтено применение данного вариатора в качестве трансформатора крутящего момента в трансмиссиях специальных колесных шасси, имеющих большую массу и значительные крутящие моменты двигателей, а именно расчетным случаем является нахождение ведомого кольца в точке С, соответствующей максимальному передаточному числу вариатора (момент начала движения), передаточное отношение и радиус кривизны в данной точке получены аналитическим путем, отвечающим требованиям точности и оперативности расчетов.
Литература:
- Степанченко Э. П., Фалалеев П. П. Технологическое оборудование.- М.: МО СССР, 1986, 364 с.
- Антонов А. С., Кононович Ю. А. и др. Армейские автомобили. Теория.- М.: Военное издательство МО СССР, 1970, 526 с.
- Пирожков Е. И. Выбор схемы и синтез фрикционной планетарной бесступенчатой передачи с разгруженными от нор нормальных контактных сил валами и подшипниками. — М.: ВВИА имени профессора Н. Е. Жуковского, 1960. — 96 с.
- Детали машин: Учебник для вузов / Л. А. Андриенко, Б. А. Байков, И. К. Ганулич и др.; Под ред. О. А. Ряховского.- 3-е изд., перераб. и доп. — М: Изд-во МГТУ им. Н. Э. Баумана, 2007. — 520с.

