Основной целью диагностирования технического состояния (ТС) является оптимальная организация процессов оценки ТС объектов и систем различной сложности. В настоящее время уменьшение экономических и трудовых затрат, сокращение времени поиска и установления причины отказа того или иного элемента системы, увеличение сложности алгоритмов и систем диагностики вызывает интерес к разработке методов и средств технической диагностики (ТД), требующих минимальных затрат на их проектирование и реализацию, а также простоту функционирования [1].
Наибольшей популярностью при решении задач ТД все чаще начинают пользоваться интеллектуальные системы, построенные на базе алгоритмов функционирования искусственных нейронных сетей (ИНС) различной архитектуры построения и специфики выполняемых задач. В данной работе рассмотрен принцип диагностирования объектов, выполняющие различные преобразования сигналов с использованием ИНС, суть функционирования которых заключается в построении неявно-выделенной функциональной зависимости данных выходных сигналов объекта контроля (ОК) от входных сигналов, тем самым решая неформализуемую задачу без априорного определения алгоритма функционирования. Рассмотрим модель выпрямительного устройства, реализованного в пакете «Simulink» среды объектно-ориентированного программирования Matlab, представленного на рисунке 1.
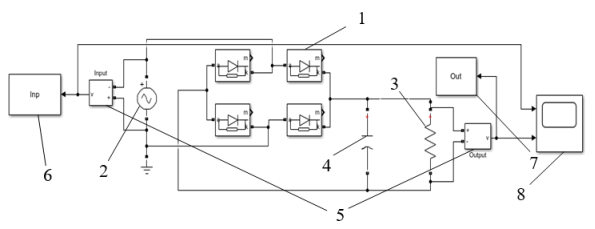
Рис. 1. Модель выпрямительного устройства: 1 — выпрямительные диоды; 2 — источник переменного тока; 3 — резистор; 4 — конденсатор; 5 — измерительные вольтметры; 6 — блок сбора обучающих входных данных; 7 — блок сбора обучающих выходных данных; 8 — осциллограф
В исправном состоянии модели выпрямительного устройства с помощью блоков «Inp» и «Out» осуществляется генерация массива эталонных обучающих данных в рабочую область Matlab при инициализации одного цикла функционирования, заданного временным рядом. После чего осуществляется обучение нейронной сети на основе обучающей выборки.
Далее производится создание двухслойной сети Элмана с массивом входов и диапазоном значений [minmax(p)], которая имеет 100 нейронов в скрытом слое и функцией активации tansig (гиперболический тангенс) и одним нейроном в выходном слое с линейной функцией активации purelin. При обучении был выбран обучающий алгоритм «Levenberg-Marquardt». Указанная сеть формируется с помощью команды:
net=newff([minmax(p)], [100 1]), затем выполняется обработка массивов обучающей выборки:
- Создание сети: Y=sim(net,Inp);
- Задание количества циклов обучения, после которых будет завершено обучение сети: net.trainParam.epoch=500;
- Задание интервала вывода информации: net.trainParam.show=100;
- Команда для выполнения процедуры обучения:
- net=train(net,Inp,Out);
- Моделирование спроектированной сети: Y=sim(net,Inp).
Завершив алгоритм обучения, структурный блок ИНС включается параллельно ОК для оценки расхождения преобразованного сигнала (рис. 2, 3).
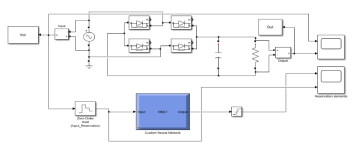
Рис. 2. Включение ИНС на параллельную работу ОК
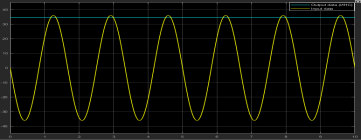
Рис. 3. График эталонного сигнала, преобразованного ИНС
Анализ графика, представленного на рисунке 3, позволяет сделать вывод о том, что такая ИНС в полной мере воспроизводит и справляется с решением задач аппроксимации функциональных зависимостей.
При возникновении неисправности в модели выпрямительного устройства, наложение сигнала от выпрямительного устройства на сигнал от ИНС позволит зафиксировать и вычислить величину отклонения напряжения выпрямительного устройства от допустимой величины, в соответствии с формулой (1) и рисунком 4.
![]() , (1)
, (1)
![]() где
где ![]() — верхняя (нижняя) граница сигнала от выпрямительного устройства;
— верхняя (нижняя) граница сигнала от выпрямительного устройства; ![]() — установившееся значение сигнала, преобразованного ИНС.
— установившееся значение сигнала, преобразованного ИНС.
![]()
![]()
![]()
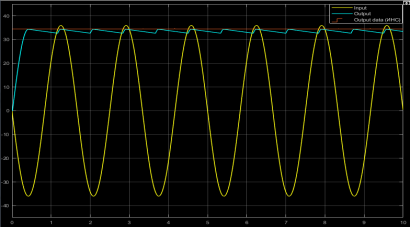
Рис. 4. Вычисление отклонения сигнала от эталонного значения
Таким образом, применение ИНС в задачах технической диагностики позволяет решать группы неформализуемых задач без априорного определения алгоритма решения с незначительной затратой трудовых и экономических ресурсов. В ближайшей перспективе интеллектуальные системы позволят осуществлять диагностику ТС объектов различной сложности и архитектуры, являясь унифицированными интеллектуальными диагностическими системами, инвариантными к любым классам и видам используемой информации.
Литература:
- Веселов О. В., Методы искусственного интеллекта в диагностике: учебное пособие / О. В. Веселов, П. С. Сабуров; Владимирский гос. ун-т им. А.Г. и Н. Г. Столетовых. ‒ Владимир: Изд-во ВлГУ, 2015. ‒ 251 с.

