Развитие технологий по работе со звуком сделало создание музыки доступным для многих людей, что привело к значительному увеличению ее количества и разнообразия. Следствием этого стало появление музыкальных потоковых сервисов, которые помогают ориентироваться в большом количестве музыки. При этом большинство музыкальных сервисов формирует рекомендации, основываясь на предпочтениях пользователей, либо используя для этого метаданные, описывающие музыку: исполнитель, название альбома, жанр, дата выхода и т. д. В данной статье предлагается метод, который бы позволял находить схожие по звучанию песни, основываясь на анализе их звуковых характеристик.
Ключевые слова: звук, музыка, рекомендательная система, частота, темп, тональность.
Совершенствование и удешевление музыкальных инструментов и звукозаписывающего оборудования, активное развитие технологий для работы со звуком, появление множества программ для создания и обработки музыки на компьютере, а также возможность дистанционного обучения через Интернет — в совокупности все это привело к значительному упрощению процесса создания музыки.
Благодаря этому появилось множество музыкантов и исполнителей, и значительно выросло количество музыки, предлагаемой слушателям. В настоящий момент в одной только библиотеке сервиса Spotify храниться более 45 млн. музыкальных композиций. Таким образом, у слушателей возникла проблема — как ориентироваться в столь значительном количестве разнообразной музыки.
В качестве решения этой проблемы появились потоковые музыкальные сервисы. Работают они по подписочной системе, предоставляя слушателям доступ ко всей своей музыкальной библиотеке за месячную абонентскую плату. Сервисы используют рекомендательные системы — те анализируют музыкальные предпочтения слушателей, и подбирают песни, которые должны им понравиться.
При этом большинство музыкальных сервисов формирует рекомендации, основываясь на предпочтениях пользователей, либо используя метаданные, описывающие музыку: исполнитель, название альбома, дата выхода, и т. д.
Существует возможность расширить список этих параметров, дополнив его параметрами, характеризующими звук музыкальной композиции: соотношение частот, тональность или число тактов в минуту. Это сделает рекомендации потоковых музыкальных сервисов более точными, а значит, и упростить пользователям поиск необходимой им музыки.
Для поиска схожих музыкальных композиций лучше всего подойдут частотный баланс, темп и тональность. Их достаточно, для того чтобы в полной мере описать песню, а также их анализ возможно автоматизировать.
Для демонстрации механизма анализа частотного баланса сравним два жанра: танцевальную и рок-музыку. Для этого проанализируем несколько музыкальных композиций, и для каждого жанра получим обобщенные графики частот.
На рисунке 1 изображены частотные балансы в жанрах рок-музыка и танцевальная музыка.
Узкой линией обозначен график танцевальной музыка, широкой линией — график рок-музыки. Прямоугольниками выделены наиболее различающиеся диапазоны частот.
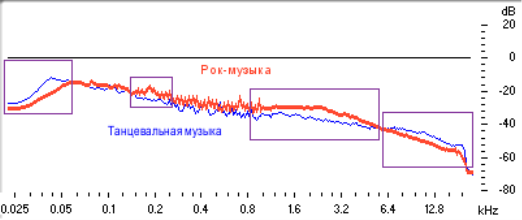
Рис. 1. Сравнение танцевальной и рок-музыки
Баланс частот музыкальной композиции будет основной характеристикой метода для поиска и сравнения песен между собой.
Для работы будут использоваться диапазон частот, в котором слышит человек — от 25 Гц до 20 кГц. Для составления частотного баланса музыкальной композиции будет использована логарифмическая шкала. Разместим на ней через равное расстояние 500 точек, каждая из которых будет обозначать соответствующую частоту. Отсчет точек будет вестись от нижней границы в 25 Гц (n = 1) до верхней границы в 20 кГц (n = 500).
Для равномерного распределения частот по логарифмической шкале была использована следующая формула:
, (1)
где F — это значение частоты n;
n — это порядковый номер частоты, имеет диапазон от 1 до 500.
На каждый отсчет дискретизации песни для каждой частоты мы будем определять уровень энергии звука. После этого мы посчитаем среднее арифметическое для уровня энергии каждой из частот. Полученная совокупность значений и будет представлять собой частотный баланс:
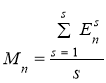, (2)
где Mn — это среднее арифметическое значение энергии звука частоты n;
n — это порядковый номер частоты, имеет диапазон от 1 до 500:
s — это номер отсчета;
— это уровень громкости частоты n в отсчете s.
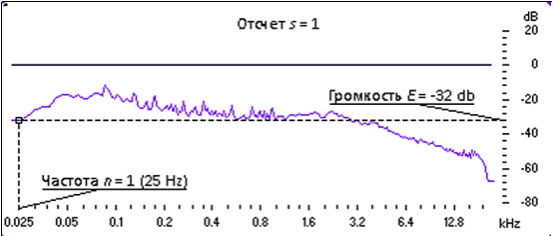
Рис. 2. Определение уровня энергии звука для частоты 25 Гц
Далее необходимо определить темп композиции. Человеческий слух определяет ритм музыки как периодическую последовательность ударов. Но звук будет слышен как удар, только если его энергия в значительной степени превосходит энергетическую историю звука, то есть если мозг обнаруживает жесткую вариацию звуковой энергии. Таким образом, ритм определяется вариацией звуковой энергии. Поэтому чтобы найти всплеск звуковой энергии — необходимо сравнивать его со средней энергией окружающего звука. При этом нет смысла сравнивать со всей музыкальной композицией, потому что в ней могут присутствовать как громкие части, так и тихие.
Для нахождения всплеска достаточно будет проанализировать отрезок песни длительностью 15 мс.
При частоте дискретизации в 44100 Гц, длительность в 15 мс составит 661,5 отсчета. Поскольку отсчеты не могут быть разделены на части, то округлим дробную величину и получим 662 отсчета. Для дальнейших расчетов она будет обозначена как c.
Посчитаем количество звуковой энергии в выделенном отрезке музыкальной композиции по формуле:
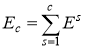, (3)
где
— это количество звуковой энергии, содержащейся в c отсчетов;
c — это количество отсчетов содержащееся в 1/64 такта;
s — это порядковый номер отсчета;
— это количество энергии звука, содержащейся в отсчете s.
Для определения ближайшей средней звуковой энергии достаточно использовать фрагмент музыки длительностью в 1 секунду или 44100 отсчетов.
Поскольку ближайшая средняя энергия звука будет сравниваться с количеством энергии для выделенного отрезка, то для этого необходимо определить, сколько таких же отрезков звука длительностью в 662 отсчета содержится в 1 секунде.
Определив общий уровень энергии звука для фрагмента в 1 с и поделив его на количество отрезков, мы найдем ближайшую среднюю энергию:
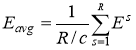, (4)
где Eavg — это ближайшая средняя энергия звука, содержащаяся в R отсчетов;
R — это частота дискретизации;
c — это количество отсчетов содержащееся в 1/64 такта;
s — это порядковый номер отсчета;
— это количество энергии звука, содержащейся в отсчете s.
Далее следует определить, насколько большой должна быть разница между количеством звуковой энергии выделенного участка и ближайшей средней энергией звука, чтобы можно было сделать вывод, что в выделенном отрезке звучит удар. Экспериментальным путем удалось выяснить, что разница в 1,3 раза является оптимальной. Обозначим ее как K.
Следовательно, удар будет слышен, если будет выполняться следующее условие:
, (5)
где — это количество звуковой энергии, содержащейся в выделенном отрезке звука;
Eavg — это ближайшая средняя энергия звука;
K — это коэффициент разницы между этими энергиями.
Обнаружив удары, мы можем вычислить время между ними, а из него рассчитать темп музыкальной композиции. Темп считается как количество четвертей такта, звучащих за минуту.
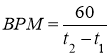, (6)
где BPM — это темп музыкальной композиции;
t1 — это время первого удара;
t2 — это время второго удара.
Поскольку данный алгоритм может обнаруживать не только удары, звучащие раз в четверть, но и в половину, и в 1/8 такта, то BPM может получиться слишком большим или маленьким. Для BPM оптимальным будет значение между 100 и 200, и чтобы темп оказался в этом диапазоне, его можно умножить, либо разделить на 2 или 4.
Тональность музыкальной композиции можно определить, если понять, какие ноты звучат в композиции. Однако, это очень сложная задача из-за того, что обычно одновременно звучит несколько нот и несколько инструментов.
В музыке существует частотный диапазон, где инструменты не смешиваются, потому что исполнители стараются сохранить в нем чистое звучание — это саб-бас. Также задачу упрощает то, что в нижних частотах очень часто звучат основные ноты тонального ряда.
Для определения нот будет использоваться диапазон частот от 25 до 63 Гц, в котором располагаются саб-басы. Частоты ниже 25 Гц человек не слышит, поэтому при микшировании музыки их обрезают для сохранения четкой слышимости басов. В этих частотах располагаются ноты контроктавы и субконтроктавы.
Каждый отсчет дискретизации определяется частота с наибольшей энергией звука, после чего определяется ближайшая к ней по частоте нота по формуле:
, (7)
где 
— это музыкальная нота, звучащая в отсчете s;
— это диапазон частот от 25 до 63 Гц;
s — это порядковый номер отсчета.
На основании нот, прозвучавших в саб-басу, определяется тональность музыкальной композиции и ее тональный лад — мажорный или минорный.
Далее необходимо сравнить музыкальные композиции отдельно по каждой из звуковых характеристик. Из полученных значений будет вычислена итоговая разница между композициями.
Для того чтобы понять, насколько две музыкальные композиции различаются по частотному балансу, следует найти у них разницу между соответствующими частотами. Поскольку важна лишь величина разницы, то она считается без учета знака:
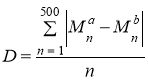, (8)
где D — это относительная разница между частотными балансами музыкальных композиций a и b;
Mn — это среднее арифметическое значение энергии звука частоты n;
a — это выбранная музыкальная композиция;
b — это музыкальная композиция, которая сравнивается с выбранной музыкальной композицией;
n — это порядковый номер частоты, имеет диапазон от 1 до 500.
Величина разницы темпов у двух музыкальных композиций будет равна отношению разницы в темпах к значению темпа выбранной композиции. Разница между темпами считается без учета знака и рассчитывается по формуле:
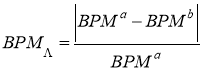, (9)
где
— это относительная разница в темпе между музыкальными композициями a и b. принимает значение от 0 до 1, где 0 означает, что у композиций одинаковый темп, а 1 означает, что темпы композиций различаются в два раза.
Далее музыкальные композиции сравниваются по тональностям. Опытным путем было установлено, что если у композиций различаются тональные лады, то итоговое значение разницы следует увеличить на 10 %. Обозначим этот параметр как 
.
Итоговая относительная разница между двумя музыкальными композициями по результатам сравнения звуковых характеристик будет считаться следующий образом по формуле:
, (10)
где G — итоговое значение разницы между двумя музыкальными композициями, принимает положительное значение, где, чем больше число, тем сильнее разница в звучании между композициями, а 0 означает, что композиции идентичны по звучанию;
L — параметр, принимающий значение 0.1, если сравниваемые композиции имеют различные тональные лады, и 0 если одинаковые.
Методика была реализована в виде компьютерного приложения для Windows, работающего с базой данных. Программой было проанализировано по разработанному методу 25 тысяч музыкальных композиций различных жанров. Музыкальные композиции имели формат MPEG-3 Layer 3 с битрейтом 320 кбит/с и частотой дискретизации 44100 Гц. Значения звуковых характеристик, полученные по результатам анализа, были загружены в базу данных.
Для проведения эксперимента было выбрано 5 музыкальных композиций разных жанров. Также было отобрано 10 испытуемых, среди которых 5 имеют оконченное начальное музыкальное образование, и был приглашен эксперт, работающий звукорежиссером, для проведения дополнительной оценки.
Испытуемые должны были загрузить 5 выбранных композиций в разработанное приложение, а также в Google Play Music и Spotify. Затем они должны были оценить первые 10 песен, предложенных каждым из сервисов на каждую из загруженных композиций. Оценивалось сходство по звучанию между загруженной музыкальной композицией и предложенной песней. Оценка производилась по шкале от 1 до 10, где 1 означает, что композиции совершенно не похожи по звучанию, а 10 означает, что композиции имеют идентичное звучание
В заключительном этапе принимал участие эксперт, который провел дополнительную оценку всех композиций, предложенных сервисами в ходе эксперимента.
Из выставленных оценок для каждого испытуемого методом нахождения среднего арифметического была рассчитана обобщенная оценка для каждого из приложений. После чего таким же способом для каждого приложения были получены оценки эксперта и итоговые оценки.
Таблица 1
Результаты эксперимента
|
Номер испытуемого |
Разработанное приложение |
Google Play Music |
Spotify |
|||
|
Оценка испытуемого |
Оценка эксперта |
Оценка испытуемого |
Оценка эксперта |
Оценка испытуемого |
Оценка эксперта |
|
|
1 |
7,1 |
6,8 |
8,2 |
8,5 |
9 |
9,5 |
|
2 |
4,9 |
6,8 |
8,2 |
8 |
9,5 |
9,2 |
|
3 |
7,8 |
6,8 |
5,8 |
8,2 |
9,5 |
9,4 |
|
4 |
4 |
6,8 |
8 |
8,2 |
10 |
9,4 |
|
5 |
5,5 |
6,8 |
9,1 |
8,4 |
9 |
9,4 |
|
6 |
6 |
6,8 |
8 |
8,5 |
10 |
9,5 |
|
7 |
7 |
6,8 |
7,4 |
8,4 |
10 |
9,5 |
|
8 |
7,5 |
6,8 |
8 |
8,3 |
9,5 |
9,3 |
|
9 |
5,2 |
6,8 |
8,5 |
8 |
9 |
9,2 |
|
10 |
7 |
6,8 |
9,8 |
8,5 |
9,5 |
9,6 |
|
Итоговый результат |
6,2 |
(+9,7 %) 6,8 |
8,1 |
(+2,5 %) 8,3 |
9,5 |
(-1,1 %) 9,4 |
Расхождения в оценках испытуемых и эксперта составили менее 10 %, что говорит о достоверности данных оценок. Эксперимент показал, что предложенный в работе метод позволяет решить проблему ориентации в больших объемах музыки. Согласно оценкам эксперта, программа, разработанная на основе предложенной методики, дает лишь на 28 % менее точные рекомендации, чем Spotify.
Разработанную методику можно использовать для совершенствования существующих музыкальных сервисов, использующих рекомендательные системы с фильтрацией по содержанию.
Литература:
1. Whitman, Brian A. Learning the meaning of music. / Brian A. Whitman // MIT Libraries. — URL: https://dspace.mit.edu/handle/1721.1/32500 (дата обращения: 30.06.2019).
2. Jehan, Tristan. Creating Music by Listening. / Tristan, Jehan // MIT Media Lab. — URL: http://web.media.mit.edu/~tristan/phd/dissertation (дата обращения: 30.06.2019).
