Формирование гигантских волн-убийц из относительно спокойного моря является одним из самых загадочных явлений не только в физической океанографии, но и во всей физике нелинейных волн. В настоящий момент обширная литература посвящена объяснению этого эффекта. Однако практически все документы по этому вопросу имеют одинаково слабое решение данной проблемы. Для описания уравнения в большинстве литературы используется формула, основанная на разложении по степеням малого параметра, нелинейное уравнение Шредингера для глубокой воды.
Однако формирование волн убийц — это одиночное событие, поэтому теории, предложенные до сих пор, не могут объяснить этот эффект. В настоящей статье сформулировано следующее предложение: будем считать, что волна- убийца является «гигантским сапуном». Поддержим эту гипотезу численным экспериментом. Стоит отметить, что в ходе эксперимента будет использовано не уравнение огибающей, а точное полное нелинейное уравнение Эйлера для потенциального потока идеальной несжимаемой жидкости со свободной поверхностью. Изучим поведение жидкости на плоскости, где одна координата горизонтальная, а другая — вертикальная.
- Базовые уравнения
Предположим, что жидкость заполняет область:
Поле скоростей рассматривается как потенциал, причем гидродинамический и представим в виде f(x,y,z). Форма поверхности воды обозначается v(x,t) и удовлетворяет уравнению:
Можно выполнить конформное преобразование, чтобы заполнить область жидкостью на плоскости Z = x+i*y нижней полуплоскости на плоскость w:
Данное преобразование реализуется хорошо известным функциями из теории функций комплексных переменных.
Потенциал f(x,t) переходит в комплексную скорость потенциала F(W,t).
Они оба, F, W, аналитические функции в нижней полуплоскости. Также будем использовать уравнение в вариациях:
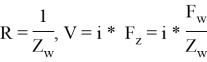
Устремим 
— периодические функции от u.
- Нелинейное уравнение Шредингера
Для слабонелинейных течений существует хорошо известное уравнение, описывающее слабомодулированную волновую цепочку или уравнение Шредингера (NLSE). Данное уравнение позволяет найти решение для волновых уравнений. Однако, в настоящей работе изучим следующую проблему: существует ли подобное решение для сильного нелинейного потока? Другими словами, попытаемся найти уравнение с очень малой несущей волной и большой высотой и крутизной.
- Численное моделирование гигантского сапуна
Для начального условия используем нелинейный сапун с крутизной:
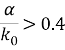
Идея для численного эксперимента заключается в изучении возможности существования дыхательных аппаратов. Достигаем этого следующим образом.
Начальное состояние. Для начальных условий используем сапун, полученный из аппроксимации NLSE. Однако его параметры были выбраны далеко за пределами применимости NLSE. Моделирование проводилось в периодической области 
. Значение α варьируется от 30 до 50.
Демпфирование. Первичный сапун NLSE изучает избыточную энергию. В моделировании использовалось демпфирование для этого излучения энергии. Данная процедура была реализована следующим образом. Во-первых, симуляция была сформирована в системе отсчета, движущийся с групповой скоростью. Данная скорость вычисляется во время имитации и настраивается так, чтобы держать сапун в центре области. Этот метод позволяет ввести затухание вблизи краев области, чтобы избавиться от избыточного излучения. Через некоторое время, когда излучение исчезает, будет уходить и затухание. Таким образом, процедура с демпфированием выглядит следующим образом:
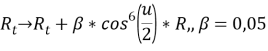
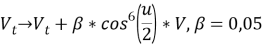
Начальное преобразование. Поскольку получилось избавиться от затухания, то можно наблюдать долговременное изменение оставшейся структуры. Здесь также стоит отметить, что рассматривается наиболее возможная нелинейная ситуация. Ниже рассмотрено моделирование с 
и α = 50. В рамках огибающей существует очень мало периодов волн. Формально это точное решение для NLSE. Как бы то ни было, крутизна настолько высока, что аппроксимация NLSE терпит неудачу. Это означает, что вовремя преобразования с этими начальными условиями должны произойти существенные изменения. Так через некоторое время первоначальный «горб» излучает энергию в течение времени, когда действует искусственное демпфирование и исчезает при Т=350, а профиль поверхности и крутизна принимают более сглаженный вид, то есть не имеют места с резко выраженными пиковыми значениями. Также можно предположить, что в это время уже начинается новая симуляция начальных условий, чтобы предсказывать появление новой волны. После более чем 2000 периодов волн ничего не происходит, тогда сапун распространяется со скоростью, которая примерно на 10 процентов больше, чем линейная групповая скорость. Также следует отметить, что крутизна всегда меньше, чем предельно значение 1/3, но может быть близка к этому значению (данное значение было получено в ходе проведения численной части работы). Данные сапуны возникают из локализованных начальных условий. Избыточное излучение остается в периодической области моделирования и не влияет на сапун. Эта ситуация схожа с уравнением NLS, которое интегрируемо.
- Заключение
Было численно показано, что строго нелинейный локализованный сапун существует на поверхности глубокой воды и распространяется в течение очень долгого времени без потери энергии. Есть все основания предполагать, что он существует. В данной работе была предложена идентификация волн-убийц с гигантскими сапунами. Однако не затрагивалась проблема, как именно появляются волны-убийцы. Данное существование является необычным в мире нелинейных волн. Для таких сапунов действительно существуют интегрируемые системы, например NLSE. Однако в неинтегрируемых системах они теряют свою актуальность из-за потери энергии.
Литература:
- Абловиц М., Сигур Х. Солитоны и метод обратной задачи. М.: Мир, 1987.
- Кудряшов Н. А. Аналитическая теория нелинейных дифференциальных уравнений. Москва-Ижевск: Институт компьютерных исследований, 2004.
- Hill, J. M., Differential Equations and Groups Methods for Scientists and Engineers, CRC Press, Boca Raton, 1992.
- Zakharov, V. E. (Editor), What is Integrability?, Springer-Verlag, 1990.
