Поглощение продольных и поперечных волн в среде является одной из важных характеристик, используемых в промысловой и разведочной геофизике. Чаше всего такие параметры определяют с помощью скважинных измерений методом акустического каротажа. Однако, если измерение затухания продольной волны Р не вызывает больших затруднений; так как она образует первые вступления, то определение поглощения поперечной волны S является более сложной задачей, поскольку она выступает на фоне сильных интерференционных колебаний, вывиваемых резонансными явлениями в скважине. Поэтому изучение распространение и поглощение продольных и поперечных волн в скважине является очень актуальной задачей.
Рассмотрим жидкий цилиндр 
находящийся в безграничной деформируемой среде 
Скорости распространяющихся волн и плотности в соответствующих средах обозначим через 
Потенционалы скоростей волн, распространяющихся в такой системе удовлетворяют волновым уравнениям
(1)
На границе раздела выполняются условия непрерывности нормальных составляющих смещений, и напряжения и равенства нулю касательных напряжений:
(2)
Дисперсионное уравнение для осесимметричных колебаний, полученное из граничных условий (2) в предложении ограниченности поля на оси цилиндра r=0 и убывания его на бесконечность, может быть записано в виде
(3)
Здесь через Jo(x), J1(x),Ko(y), К1(у) обозначены функции Бесселя нулевого первого порядка, а такие функции Макдональда: а1и а2 определяются соотношениями
Остальные обозначения следующие:
где 
- фазовая скорость волн.
Предположим,что обе среды характеризуются малым поглощением, которое можно ввести, считая комплексными величинами,мнимая часть которых определяет затухание:
(4)
Уравнение (3) для нахождения затухания нормальных волн, приравнивая к нулю мнимую часть
где
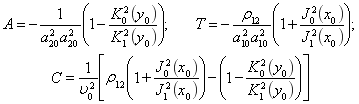
Рассмотрим отдельно зависимость от частоты коэффициентов М и N при 
и
, выходящих в выражение (5):
(6)
Коэффициент М будет полностью характеризовать затухание нормальной волны, вызванное потерями в окружающей среде,если предположить, что жидкость в цилиндре идеальная, т. е.=0.
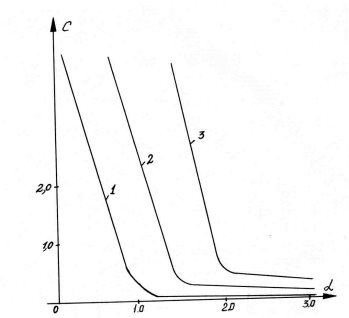
Рис.1. Зависимость фазовой скорости от волновых чисел
Пусть выполняемое неравенство а<<1 и Kr0a2находится вблизи своих граничных значений, с которых начинается п -я нормальная волна. Из уравнения (3) следует, что граничные значения оказываются равными корням xn(и=1,2...) функции Бесселя J1(xn)=0. Тогда из первого равенства в соотношениях (6) будет иметь lim m=1, α2
0 т. е. затухание нормальных волн при критических частотах оказывается равным затуханию волн в окружающей среде. На рис. 1. приведена зависимость фазовой скорости от волновых чисел. Из рисунка видно что, с увеличением волновых чисел дисперсионные кривые приближаются к асимтотике.
Литература:
- Сафаров И. И. Колебания и волны в диссипативно неоднородных средах и конструкциях. Тошкент,1992.
- Крауклис П. В., Молотков Л. А. К теории сейсмического каротажа в обсаженных скважинах. — Изд. Ан СССР. Физика Земли, 1968, N9, — С.39–46.
