Ключевые слова: модель надежности, изменяющаяся интенсивность отказов, марковский процесс, система нелинейных дифференциальных уравнений.
Для расчета характеристик надежности сложных систем используют динамические модели. Если поведение системы можно описать марковским процессом, то математическая модель надежности такой системы — система дифференциальных уравнений. В работах по надежности, например, [1, с.127] рассматривается функционирование восстанавливаемых систем при условии пуассоновского закона распределения потоков отказов и восстановления (интенсивность потока отказов λ(t) и интенсивность восстановления μ(t) — константы), математическая модель такой системы — система обыкновенных дифференциальных уравнений (ОДУ). Решение системы ОДУ находится аналитически или численно.
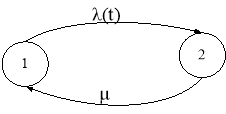
Рис. 1. Марковский граф восстанавливаемого элемента
В работе рассматривается случай, когда интенсивность потока отказов λ(t) является функцией времени. На рис. 1 приведен марковский граф восстанавливаемого элемента, математическая модель — система нелинейных ДУ
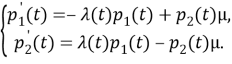
Если строить марковские модели надежности систем, состоящих из нескольких восстанавливаемых элементов, то пространство состояний модели будет увеличиваться. Система дифференциальных уравнений относительно Pi(t) (i = 1, 2, …, n) в общем виде записывается как
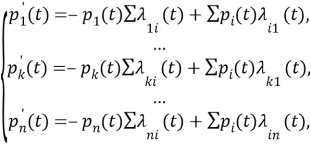
где первая сумма в правой части уравнения содержит интенсивности переходов из текущего состояния k, а вторая — интенсивности переходов в состояние k, переходы, соответствующие отказам, имеют коэффициенты, зависящие от времени, переходы, соответствующие восстановлению работоспособности — константы.
Аналитическое решение системы нелинейных ДУ в общем случае получить сложно, поэтому для решения необходимо использовать численные методы. Система Matlab предоставляет набор средств для решения систем ДУ.
Предложенная модель использована для расчета показателей надежности дублированной системы с восстановлением, на рис. 2 приведен марковский граф системы. Состояния графа:
− S0 — элементы 1 и 2 работоспособны, система работоспособна;
− S1 — элемент 1 неработоспособен, элемент 2 работоспособен, система работоспособна;
− S2 — элемент 1 работоспособен, элемент 2 неработоспособен, система работоспособна;
− S3 — элементы 1 и 2 неработоспособны, система неработоспособна.
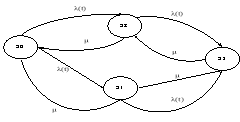
Рис. 2. Марковский граф дублированной системы с восстановлением
Этому графу соответствует система уравнений
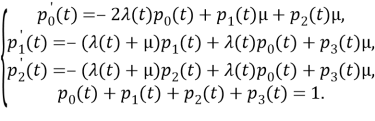
Здесь уравнение для р4(t) заменено нормирующим. Систему уравнений можно преобразовать к виду
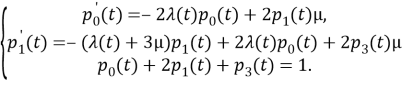 ,
,
которой соответствует марковский граф, показанный на рис. 3. В этой модели состояние S1 — объединенное состояние, соответствующее отказу одного из элементов системы, при этом вся система является работоспособной.
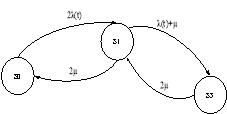
Рис. 3. Марковский граф укрупненной системы
Для модели рис. 3 был рассчитан коэффициент простоя, результаты приведены в таблице 1, для сравнения в таблице приведены результаты для восстанавливаемого элемента без резервирования (модель рис.1).
Таблица 1
Коэффициент простоя
|
Система |
μ= 0,01 |
μ=0,1 |
μ=1 |
μ=10 |
|
|
Без резервирования с восстановлением |
3,15*10–3 |
3,16*10–4 |
3,16*10–5 |
3,16*10–6 |
|
|
Дублированная с восстановлением |
4,70*10–3 |
4,74*10–4 |
4,74*10–5 |
7,74*10–6 |
|
Как видно из таблицы, коэффициент простоя линейно убывает с увеличением μ и для системы без резервирования, и для системы с резервированием (дублированием) с одним и тем же коэффициентом. Дублированная схема реализуется удвоенными аппаратными затратами, при этом характеристики надежности различаются на 30 % (коэффициент 0,3). В системах без восстановления показатели надежности системы без резервирования и дублированной системы различаются на порядок, т. е. в системах с восстановлением использование резервирования дает гораздо меньший эффект по сравнению с системами без восстановления, применение резервирования в восстанавливаемых системах нецелесообразно.
Литература:
- Викторова, В. С. Модели и методы расчета надежности технических систем / В. С. Викторова, А. С. Степанянц; 2-е изд., испр. — М.: ЛЕНАНД, 2016. — 256 с.







