Определение воздействия внутренних и внешних угроз на информационную систему персональных данных с помощью построения математической модели
Авторы: Рогова Олеся Сергеевна, Юрьев Дмитрий Русланович
Рубрика: 1. Информатика и кибернетика
Опубликовано в
Дата публикации: 07.07.2018
Статья просмотрена: 86 раз
Библиографическое описание:
Рогова, О. С. Определение воздействия внутренних и внешних угроз на информационную систему персональных данных с помощью построения математической модели / О. С. Рогова, Д. Р. Юрьев. — Текст : непосредственный // Технические науки: проблемы и перспективы : материалы VI Междунар. науч. конф. (г. Санкт-Петербург, июль 2018 г.). — Санкт-Петербург : Свое издательство, 2018. — С. 15-16. — URL: https://moluch.ru/conf/tech/archive/288/14435/ (дата обращения: 25.04.2024).
Каждая информационная система в той или иной степени имеет свои особенности в работе. Для того что бы дать формализованное описание структуры и процесса функционирования информационной системы необходимо создать математическую модель. Математическая модель позволяет представить процесс функционирования системы в виде, допускающем аналитическое исследование системы с использованием методов, разработанных в рамках данного математического аппарата, что в свою очередь позволяет идентифицировать неисправности, уязвимости и недостатки данной информационной системы. Основными требованиями к построенной модели являются ее достаточность для решения поставленных задач и практическая целесообразность (удобство в использовании).
Цель данной работы — на основе типичной информационной системы по обработке персональных данных построить математическую модель воздействия угроз и разработать методику их выявления.
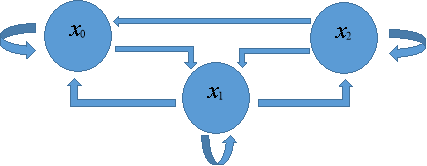
Рис. 1. Состояние системы
Данную информационную систему будем рассматривать как систему массового обслуживания, в которую поступают угрозы. Для начала рассмотрим вариант того что на систему поступают угрозы одного типа, учитывая, что данная угроза не может быть реализована или наступить несколько раз в один и тот же момент времени. Согласно этим условиям мы строим ориентированный граф (рис. 1) который показывает три различных состояния системы: а) начальное состояние (угрозы не было); б) измененное состояние (нереализованная угроза); в) критическое состояние (реализованная угроза).
Для построения математической модели системы об условимся, что у данной системы отсутствуют поглощающие состояния, т. е. реализованная угроза либо никак не влияет на работоспособность системы в целом, либо выводит из строя на непродолжительный срок один из ее сегментов. Это указывает на то, что система из любого состояния имеет возможность вернуться в исходное состояние, что позволяет нам изучить ее поведение в течении длительного промежутка времени.
Переход системы из состояния в состояние показан с помощью ориентированного графа на рис.1. Данная информационная система является системой с восстановлением, т. к. согласно вышеупомянутому она не имеет поглощающие состояния, а это означает, что из состояния Х2 система может вернуться в исходное состояние. Для описания процесса перехода системы построим матрицу интенсивностей перехода [1]:
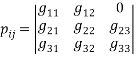 (1)
(1)
Согласно условиям, предъявляемым к матрице интенсивностей перехода [1], все элементы этой матрицы должны удовлетворять условию 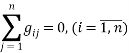 , получим:
, получим:
![]()
![]() (2)
(2)
В данной работе используется вероятностно-аналитический способ определения элементов матрицы интенсивностей переходов в соответствии с видом информационной системы (рис.1). Для определения вероятностей ![]() строим систему дифференциальных уравнений с начальными условиями
строим систему дифференциальных уравнений с начальными условиями
![]() (3) которая имеет следующий вид:
(3) которая имеет следующий вид:
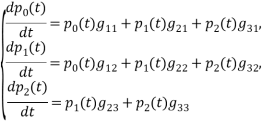 (4)
(4)
Данную математическую модель (3), (4) рассматриваемой информационной системы, можно численно решить с помощью задачи Коши с использованием специальных математических программ (например, SMath Studio Cloud)
Если переход системы из состояния в состояние осуществляется в строго определенный момент времени t, т. е. является дискретным, то матрица вероятностей перехода из состояния в состояние за один шаг имеет вид (1), иначе матрица за n- шагов (t=n) приобретает следующий вид [3,4]:
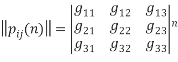 (5)
(5)
Таким образом данная математическая модель определяет воздействия внутренних и внешних угроз на информационную систему персональных данных.
Литература:
1. Алиев Т. И. Основы моделирования дискретных систем: учебное пособие. — СПб: СПбГУ ИТМО, 2009. — 363 с.
2. Волков И. К., Зуев С. М., Цветкова Г. М. Случайные процессы: учебник для вузов / под ред. В. С. Зарубина, А. П. Крищенко. — М.: МГТУ им.Баумана, 1999. — 448с.
3. Теоретические основы анализа и оценки влияния внутренних угроз на безопасность конфиденциальной информации: монография / А. П. Росенко. — М.: Гелиос АРВ, 2008. — 154 с
Похожие статьи
Моделирование систем защиты информации. Приложение...
В статье рассматриваются основные теории и методы моделирования систем защиты информации (СЗИ). Автор останавливает внимание на применении математической теории графов к моделированию СЗИ и предлагает собственную модель, реализующую подход...
Принцип квазиэквивалентного укрупнения состояний марковских...
Состояние системы в момент времени t описывается вектором x(t) = (x1(t), x2(t)), где x1(t)ϵ{0, 1} — число неисправных ЭВМ; x2(t)ϵ{0, N} — число задач в очереди и ЭВМ. Граф переходов марковского процесса x(t) имеет структуру, показанную на рис. 2а.
Представление знаний о процессах с помощью многократных...
Широкополосная приемная система станции РЭБ.
переходной процесс, электрические цепи, метод пространства параметров, матрица перехода, граф переменных состояний.
Основные принципы проектирования сложных технических систем...
Исходная модель сложной системы дает лишь наиболее общее представление (метод представления) и строится на начальном этапе проектирования; не содержит
Вероятность того, что в момент t число не разрушенных авиабомб равна m при определится в виде.
Математическое моделирование взаимодействия ионов...
Аналогично построена матрица перехода от инерциальной системы координат к подвижной.
На начальный момент времени поступательную и угловую скорости каждой частицы определим равными нулю.
Математическое и компьютерное моделирование...
Реализацией является графический редактор, реализованный в виде web-приложения (рисунок 2).
Атрибутом элемента является состояние (закрыт/открыт) (рисунок 3)
Основные термины (генерируются автоматически): система, математическая модель, атрибут элемента...
Моделирование многопараметрических систем на основе...
Моделируем ли мы поведение робота или финансовой организации, и в том и в другом случае мы имеем дело с множеством параметров, характеризующих состояние системы в некоторый момент времени.
Задача анализа загрузки сервера информационной системы...
Граф связи состояний с интенсивностями переходов представлен на рисунке 2.
, . (2). В каждый момент времени должно выполняться условие вида: . (3). Учитывая (3), отбросим в (1) второе уравнение, а в первое подставим вместо ее выражение
К расчёту переходных процессов в линейных электрических...
Записываем матрицу перехода. С помощью графа переменных состояния цепи может быть найдена не только матрица перехода , но и
Ключевые слова: математическая модель, переходные процессы, численное решение дифференциальных уравнений, электропривод...
Похожие статьи
Моделирование систем защиты информации. Приложение...
В статье рассматриваются основные теории и методы моделирования систем защиты информации (СЗИ). Автор останавливает внимание на применении математической теории графов к моделированию СЗИ и предлагает собственную модель, реализующую подход...
Принцип квазиэквивалентного укрупнения состояний марковских...
Состояние системы в момент времени t описывается вектором x(t) = (x1(t), x2(t)), где x1(t)ϵ{0, 1} — число неисправных ЭВМ; x2(t)ϵ{0, N} — число задач в очереди и ЭВМ. Граф переходов марковского процесса x(t) имеет структуру, показанную на рис. 2а.
Представление знаний о процессах с помощью многократных...
Широкополосная приемная система станции РЭБ.
переходной процесс, электрические цепи, метод пространства параметров, матрица перехода, граф переменных состояний.
Основные принципы проектирования сложных технических систем...
Исходная модель сложной системы дает лишь наиболее общее представление (метод представления) и строится на начальном этапе проектирования; не содержит
Вероятность того, что в момент t число не разрушенных авиабомб равна m при определится в виде.
Математическое моделирование взаимодействия ионов...
Аналогично построена матрица перехода от инерциальной системы координат к подвижной.
На начальный момент времени поступательную и угловую скорости каждой частицы определим равными нулю.
Математическое и компьютерное моделирование...
Реализацией является графический редактор, реализованный в виде web-приложения (рисунок 2).
Атрибутом элемента является состояние (закрыт/открыт) (рисунок 3)
Основные термины (генерируются автоматически): система, математическая модель, атрибут элемента...
Моделирование многопараметрических систем на основе...
Моделируем ли мы поведение робота или финансовой организации, и в том и в другом случае мы имеем дело с множеством параметров, характеризующих состояние системы в некоторый момент времени.
Задача анализа загрузки сервера информационной системы...
Граф связи состояний с интенсивностями переходов представлен на рисунке 2.
, . (2). В каждый момент времени должно выполняться условие вида: . (3). Учитывая (3), отбросим в (1) второе уравнение, а в первое подставим вместо ее выражение
К расчёту переходных процессов в линейных электрических...
Записываем матрицу перехода. С помощью графа переменных состояния цепи может быть найдена не только матрица перехода , но и
Ключевые слова: математическая модель, переходные процессы, численное решение дифференциальных уравнений, электропривод...











