Марковские случайные процессы нашли широкое применение при математическом моделировании динамики функционирования сложных систем [1].
Будем рассматривать поведение сложной системы (системы управления оружием или войсками, системы передачи или извлечения информации, комплекса или средств радиоподавления) в процессе выполнения ею своих функциональных задач как случайный процесс смены состояний. Если при этом вероятностные характеристики перехода из одного состояния в другое будут зависеть только от настоящего состояния и не зависеть от развития процесса смены состояний в прошлом, то для моделирования такой системы может быть использован математический аппарат марковских случайных процессов.
Однако с увеличением количества элементов в системе резко возрастает число ее возможных состояний и соответственно увеличивается количество дифференциальных или алгебраических уравнений в математической модели. Решение большого числа (например,
) дифференциальных или алгебраических уравнений даже с применением ЭВМ является затруднительным и практически невозможным. Кроме того, даже если удалось бы получить решение этих уравнений и найти вероятности состояний системы, то полученные результаты были бы труднообозримыми и неприемлемыми для принятия решений.
Для моделирования систем с большим количеством состояний применяется метод динамики средних. Этот метод позволяет определять не вероятности состояний, а характеристики случайных процессов, протекающих в изучаемых системах (например, среднее количество элементов, находящихся в одинаковом состоянии). В практике изучения систем с большим количеством состояний моделирование по методу динамики средних наиболее часто производится с целью определения математического ожидания 
и дисперсии 
численности элементов системы, находящихся в 
-м состоянии.
При выводе аналитических зависимостей для метода динамики средних учитываются следующие ограничения:
- В моделируемой системе протекает марковский случайный процесс.
- Каждый элемент изменяет свои состояния независимо от других.
- Элементы системы предполагаются однородными.
Задача моделирования динамики функционирования реальной системы по методу динамики средних формулируется следующим образом. Пусть система 
состоит из 
элементов, каждый из которых может находиться в любом из возможных состояний 
.Обозначим через 
— число элементов системы 
, находящихся в момент времени 
в состоянии 
.Требуется определить основные неслучайные характеристики случайной функции 
: математическое ожидание 
и дисперсию 
Для определения искомых характеристик случайной функции 
необходимо установить зависимость численности состояния 
от состояния каждого 
-го элемента. Имеем
где 
если 
-й элемент находится в состоянии 
и 
— в противном случае. Обозначим далее 
Так как все элементы однородны, то вероятности пребывания каждого из них в состоянии 
в любой момент времени 
одинаковы, поэтому
Очевидно, что 
а 
В силу предполагаемой независимости случайных величин 
имеем
Отсюда, в частности, следует, что для получения уравнений для нахождения 
нужно записать систему уравнений Колмогорова для вероятностей состояний 
, умножить обе части каждого из уравнений на 
и заменить 
на 
.
Систему уравнений динамики средних относительно 
естественно решать при следующих начальных условиях:
Таким образом, уравнения динамики средних являются математической моделью системы с большим количеством элементов.
Построим математическую модель для определения средних численностей состояний радиоэлектронных средств отдельного полка, при условии, что общая численность средств равна 
а каждое из них может находиться в одном из следующих состояний: 
— РЭС исправно; 
– неисправно, ведется поиск неисправностей; 
— неисправность обнаружена, ведется осмотр РЭС; 
– РЭС ремонтируется в части; 
– РЭС ремонтируется на заводе; 
— РЭС списывается и заменяется новым.
Размеченный граф изменения численностей состояний однотипных радиоэлектронных средств отдельного полка для рассматриваемых условий приведен на рисунке 1.
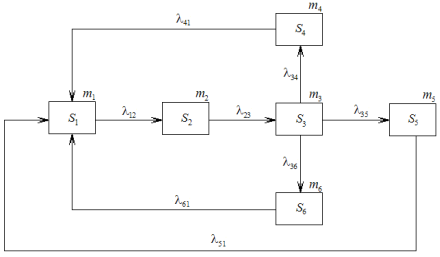
Рис. 1. Граф изменения численностей состояний однотипных РЭС
Система уравнений динамики средних для рассматриваемой задачи имеет следующий вид:
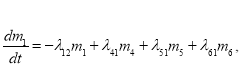
Кроме того, имеет место равенство
для любого момента времени 
.
Анализ графа состояний показывает, что предельные вероятности существуют. Запишем систему линейных алгебраических уравнений для их нахождения. Имеем
,
,
.
.
Положим 
и заменим первое уравнение условием сохранения общей численности элементов. Получим систему уравнений
,
Эта система имеет следующее решение:
Определим дисперсии численностей состояний:
Средние квадратичные отклонения численностей состояний равны:
Заметим, что, зная математические ожидания и средние квадратичные отклонения численностей состояний, мы получаем возможность оценивать также и вероятности различных состояний системы в целом, то есть, например, вероятность того, что численность какого-то состояния будет заключена в определенных пределах. Действительно, предположим, что число элементов 
велико. Тогда численность какого-то (k-го) состояния можно приближенно считать распределенной по нормальному закону. Отсюда следует, что вероятность того, что случайная величина 
(численность k-го состояния) будет заключена в каких-то границах от 
до 
, будет выражаться формулой:
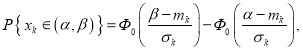
где 
математическое ожидание и среднее квадратичное отклонение численности k-го состояния, 
функция Лапласа.
Литература:
- Вентцель Е. С. Исследование операций. — М.: Советское радио, 1972. — 552 с.
