Синтез многолучевых однозазорных и двухзазорных клистронных резонаторов с кратными резонансными частотами

Наиболее широкая область применения мощных приборов СВЧ (магнетронов, клистронов, клистродов) – использование в бытовых целях. Для разнообразных технологических процессов (сушки, размораживания, вулканизации, пастеризации, спекания, разрушения твердых веществ, обжига и многих других) требуется мощность от единиц до сотен киловатт в непрерывном режиме.

Проведенное в работе [1] сопоставление перспектив применения клистронов и магнетронов в промышленных технологических установках для нагрева с уровнем мощности от 10 до 100 кВт показало, что в непрерывном режиме современные магнетроны, предназначенные для такого применения, имеют мощность < 10 кВт, КПД ~ 60-70%, срок службы 2000-3000ч и низкую стабильность. Клистроны аналогичного назначения имеют выходную мощность от 15 до 100 кВт, КПД ~ 70-80%, срок службы 30000-50000ч и хорошую стабильность. Высокий КПД таких приборов достигается введением в конструкцию резонаторной системы дополнительных резонаторов, имеющих собственные частоты, равные второй гармонике электронного тока. Однако это увеличивает габариты и массу такого устройства. Устранить этот недостаток можно за счет применения вместо двух резонаторов одного резонатора, настроенного на две кратные резонансные частоты.

Однако для многолучевых конструкций приборов СВЧ такие резонаторы пока не исследовались и не применялись. Поэтому основной задачей настоящей работы является разработка методики синтеза многоканальных резонаторов с кратными частотами.

Синтез однозазорных резонаторов с кратными резонансными частотами

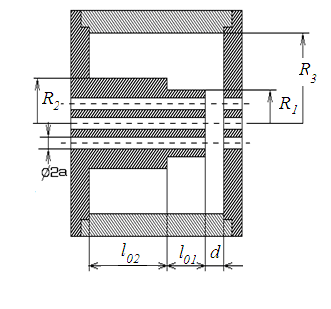
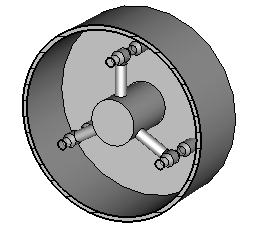
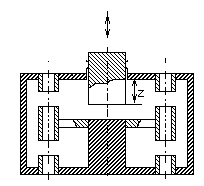
Известен ступенчато-неоднородный коаксиальный однозазорный резонатор однолучевого клистрона, настраиваемый на основную частоту (ТЕМ-вид колебаний) и ее вторую гармонику (обертон) за счет оптимального выбора его геометрических размеров [2]. Однако для многолучевых резонаторов (рис.1), предложенные в этой работе расчетные соотношения не позволяют обеспечить кратность резонансных частот.

Рис. 1. Конструкция многоканального резонатора клистрона.

Поскольку целью работы является разработка методики синтеза дуальных резонаторов, настроенных одновременно на основную и удвоенную рабочие частоты, и, так как синтез таких резонаторов численными методами, основанными на решении уравнений Максвелла, чрезвычайно трудоемок, то для решения поставленной задачи использовался метод эквивалентной схемы, согласно которому резонатор можно представить в виде эквивалентной ступенчато-неоднородной длинной линии, образованной отрезками и с волновыми сопротивлениями и . 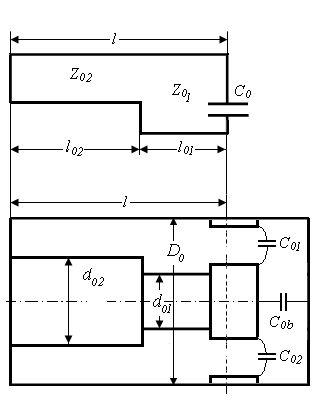Эта линия замкнута на одном конце, а на другом конце она нагружена на емкость зазора С₀ (рис.2).

Рис.2 Эквивалентная схема резонатора

Входную проводимость короткозамкнутого отрезка линии в сечении 2-2 можно рассчитать по формуле

, (1)

где C_n – емкость неоднородности линии, включенная в месте расположения скачка сопротивлений, .

Входную проводимость отрезка линии, нагруженной на реактивную проводимость 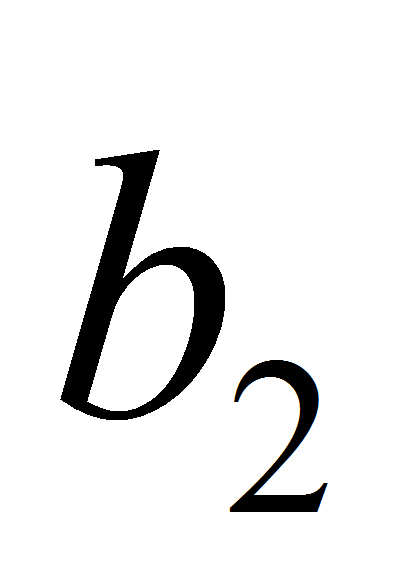, можно рассчитать с помощью уравнения

, (2)

где .

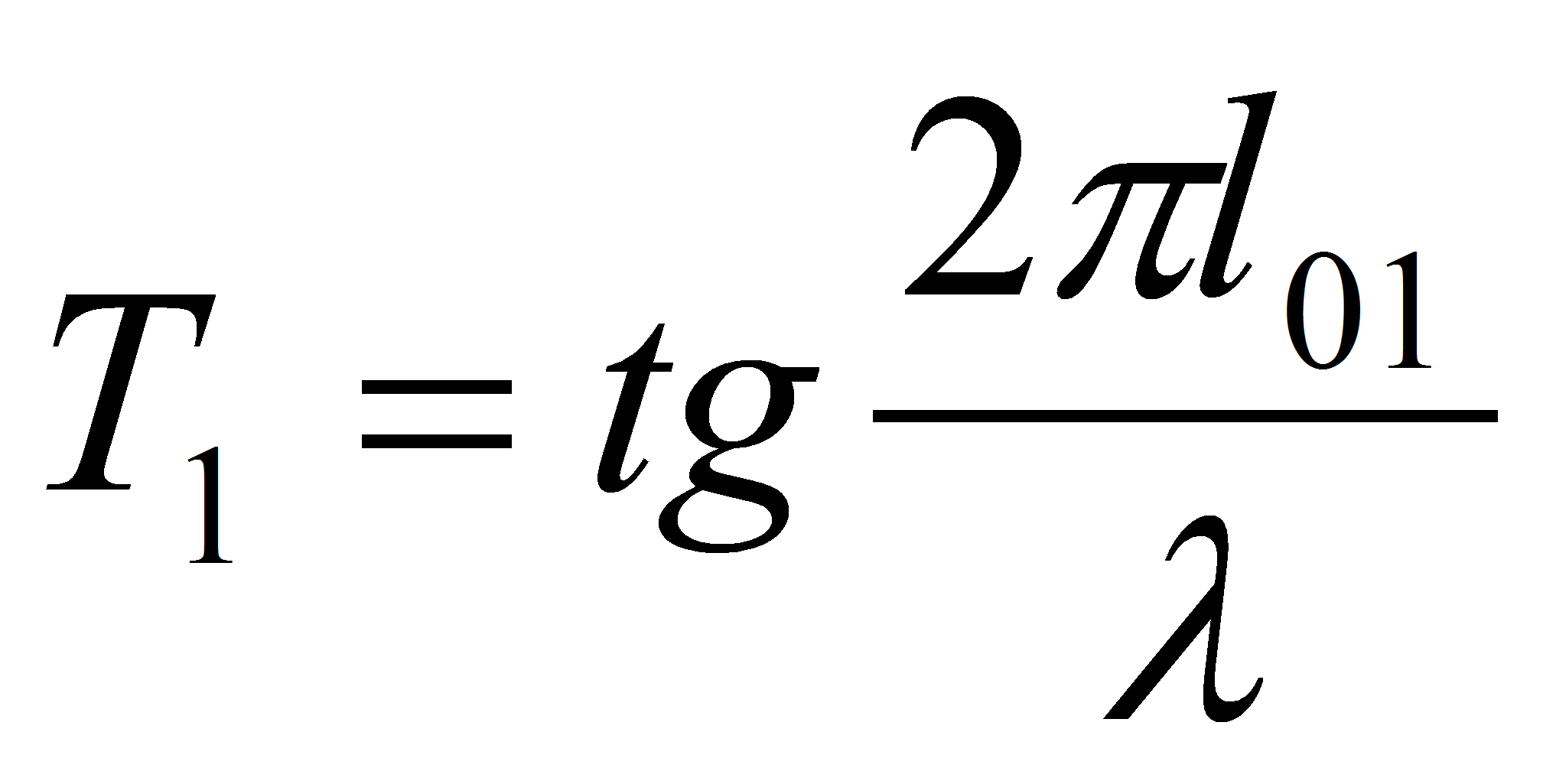Условие резонанса для такой линии может быть записано как сумма реактивных проводимостей в сечении 1-1.

= =0. (3)

Суммарная нормированная проводимость в сечении 1-1 может быть записана в виде

=0. (4)

Проведенные исследования показали, что для синтеза дуального резонатора необходимо выбирать параметры эквивалентной схемы, согласно приведенным ниже значениям критериев подобия:

, , =0.472 , (5)

, . (6)

где .

Исходными для расчета являются требуемое значение основной рабочей длины волны и волновое сопротивление . Остальные размеры вычисляются по следующим уравнениям:

(7)
(8)

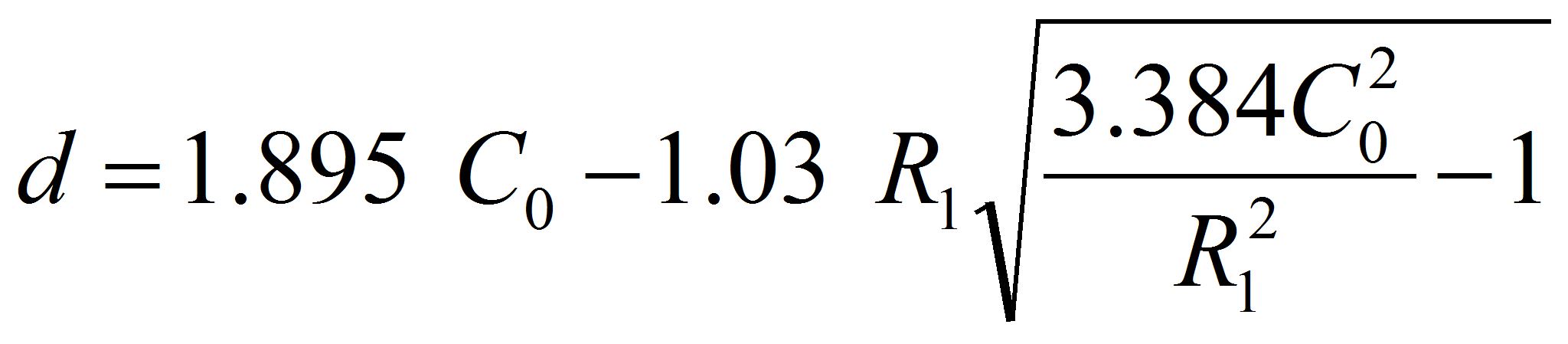(9)
В этих формулах размеры даны в см, величина емкости – в пФ.

На основе изложенной выше методики расчета была разработана специальная программа синтеза резонаторов. С помощью этой программы были рассчитаны резонаторы, предназначенные для возбуждения частот 2450, 915, 775 и 430МГц, а также для высших частот с кратностью 2. Результаты, полученные с помощью программы, приведены в таблице 1.

Таблица 1

Результаты расчета геометрических размеров резонаторов по разработанной программе

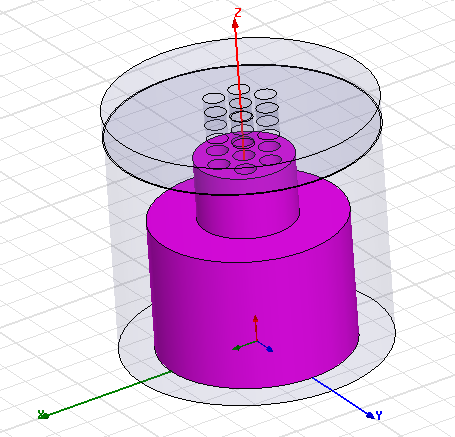
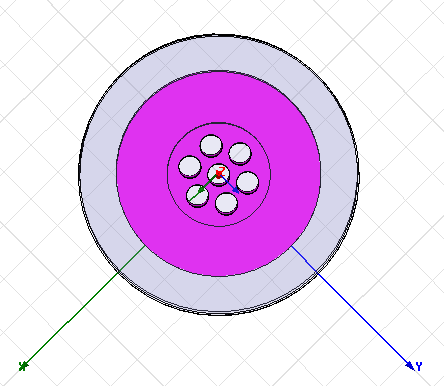
Далее, необходимо было проверить результаты расчета программы. Для этого по данным геометрическим размерам в программе HFSS были созданы модели резонаторов (рис. 4) и проведен численный эксперимент. Результаты численного эксперимента приведены в таблице 2.

Рис. 3. Модель многолучевых однозазорных резонаторов

Таблица 2

Результаты расчета собственных частот резонаторов.

В таблице №2 F₁ и F₂ – частоты, рассчитанные в программе HFSS в соответствии с геометрическими размерами, указанными в таблице №1. Как видно из таблицы 2, с помощью указанной выше методики, нам удалось добиться кратности собственных частот в соотношении 1:2. Погрешность вычислений не превышает 0.5%. Таким образом, с помощью разработанной программы можно оперативно синтезировать резонаторы с двумя необходимыми рабочими частотами, не прибегая к трудоемким численным расчетам или эксперименту.

Синтез двухзазорных резонаторов с кратными резонансными частотами

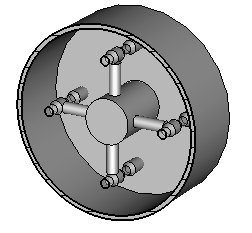
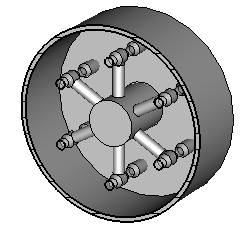
Конструкции пространственно-развитых 3-х, 4-х и 6-ти лучевых резонаторов древовидного типа схематически представлены на рис. 4.

Рис. 4. Модели 3-х, 4-х и 6-ти лучевых резонаторов.

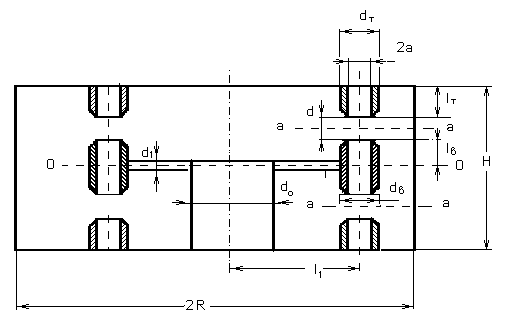
Эти резонаторы содержат в одном цилиндрическом корпусе несколько резонансных ветвей, оканчивающихся пролетными втулками. Резонансные ветви имеют вид стержней и крепятся на общем опорном стержне, короткозамкнутом на корпус прибора. Поперечное сечение резонатора с указанием основных характерных размеров приведено на рис. 5.

Рис. 5. Поперечное сечение резонатора с указанием основных характерных размеров.

Применение численных методов для расчета таких резонансных систем затруднено из-за сложной формы и отсутствия аксиальной симметрии. Экспериментально эти резонаторы, из-за новизны, также не исследованы. В связи с этим были проведены исследования по изучению электродинамических свойств новых типов резонаторов.

Исследовались резонаторы прибора со следующими размерами: H=58 мм, =9 мм, =7.4 мм, =15 мм, 2R=120мм. Пролетные втулки имели пролетные каналы диаметром 6 мм. Перестройка резонаторов осуществлялась введением специального подстроечного элемента (стержня) в максимум электрического поля резонатора. Перестройку частоты противофазного вида колебаний можно эффек­тивно осуществлять емкостным элементом в виде стержня (рис.6). Зависимость удвоенной частоты противофазного вида колебаний и частоты синфазного вида колебаний, соответствующих первой и второй собственным модам резонатора, соответственно, от длины подстроечного емкостного элемента Z, показана на рис. 7. Зависимость построена для 3-х лучевого резонатора. Видно также, что частота синфазного вида колебаний при такой перестройке изменяется слабо, по сравнению с противофазным видом.

Рис. 6. Поперечное сечение резонатора с емкостным элементом в виде стержня.

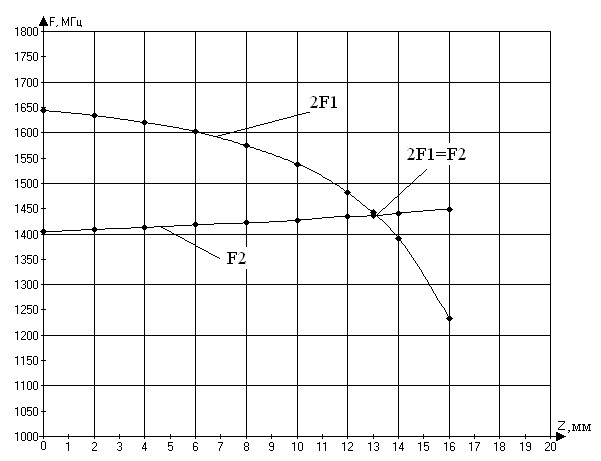
Рис. 7. Сравнение численного расчета частоты противофазного F₁ и синфазного F₂ типов колебаний для 3-х лучевого двухзазорного резонатора для разных значений длины емкостного подстроечного элемента Z.

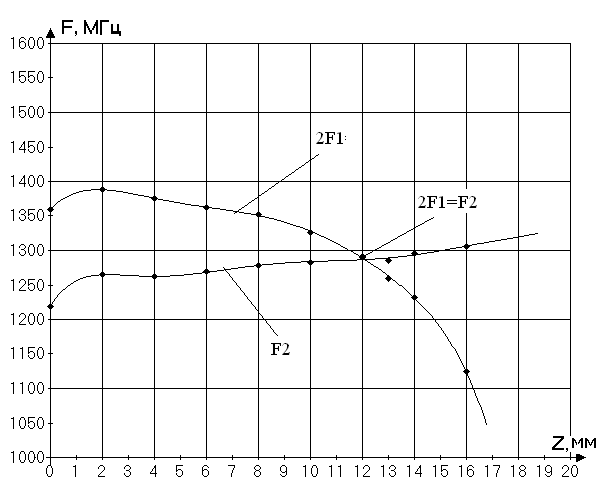
Также, были произведены расчеты для 6-ти лучевого двухзазорного резонатора. Зависимость удвоенной частоты противофазного вида колебаний и частоты синфазного вида колебаний, соответствующих первой и второй собственным модам резонатора, соответственно, от длины подстроечного емкостного элемента Z, показана на рис. 8.

Рис. 8. Сравнение численного расчета частоты противофазного F₁ и синфазного F₂ типов колебаний для 6-ти лучевого двухзазорного резонатора для разных значений длины емкостного подстроечного элемента Z.

Таким образом, как видно из рис. 7 и 8, за счет оптимального выбора размеров резонаторов и введения емкостного подстроечного элемента удалось подстроить основной противофазный вид колебаний (частота - F₁) и синфазный тип колебаний Е₀₁₀ (частота-F₂) на кратные резонансные частоты (F₂ = 2F₁) для 3-х и 6-ти лучевого двухзазорных резонаторов. При этом можно (так же как и для однолучевых приборов) обес­печить приемлемые условия для взаимодействия пучка с полем одновременно на двух гармониках.

Заключение.

Применение многоканальных дуальных резонаторов позволяет осуществить дополнительное нелинейное группирование электронного потока в многолучевых клистронах и клистродах и, тем самым, повысить их КПД не увеличивая габариты и массу приборов. С помощью разработанной программы можно оперативно синтезировать однозазорные многолучевые резонаторы с двумя необходимыми рабочими частотами, не прибегая к трудоемким численным расчетам или эксперименту.

Также была осуществлена подстройка частоты противофазного F₁ и синфазного F₂ типов колебаний для 3-х лучевого и 6-ти лучевого двухзазорных резонаторов для разных значений длины емкостного подстроечного элемента Z.

Проведенные исследования создают возможности создания на основе таких резонаторных систем но­вых типов высококачественных многолучевых СВЧ-приборов. Данные типы многочастотных приборов могут найти применение в системах связи, использующих дополнительный связной канал для дублирования передаваемой информации, а также в умножителях частоты СВЧ сигнала.

Литература:

1. Пчелинцев Г.А., Сальникова Д.А., Царев В.А. Перспектива применения клистродов для целей СВЧ энергетики// Радиотехника и связь: Материалы Международной научно-технической конференции, Саратов 18-20 мая, 2005, с. 382-385.

2. Tsarev V.A. Investigation of the electrodinamic characteristics for double-gap multi –beam klystrons cavities. / Tsarev, V.A., A.Y.Miroshnichenko,V.Y. Muchkaev // Proceedings IEEE International Vacuum Electronics Conference. US, Monterey, CA 93940, 18-20 May, 2010, p.148.

3. High-power, high-efficiency klystrons for industrial heating / Arai Shintaro, Maruyama Yoshifumi, [3] Tomikawa Kunihiro, Makino Toshimoto // NEC Res. and Dev. – 1995. – 36. №3. – с. 400 – 4005. – Англ.

4. Пат. SU 1376828 A1 H 01 J 23/18. Резонатор СВЧ-прибора/ В.Г. Андреев, Н.В. Андреев, В.М. Белугин и И.А. Сытченко, 07.10.91. Бюл. №37.