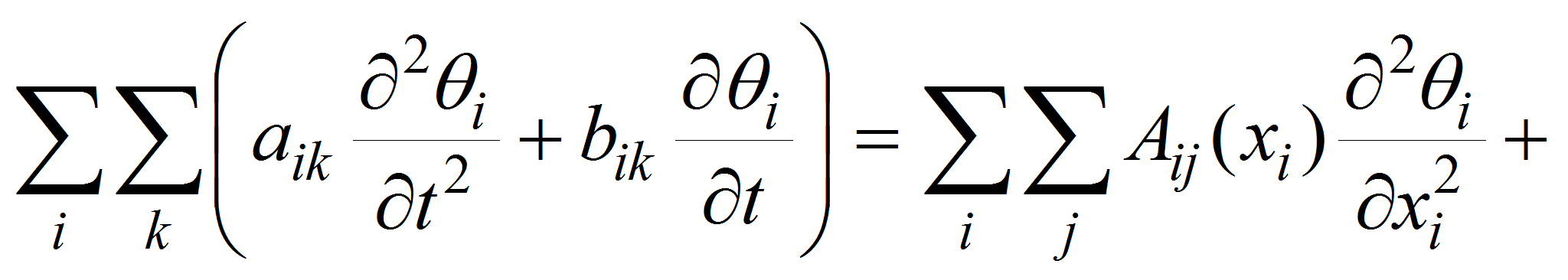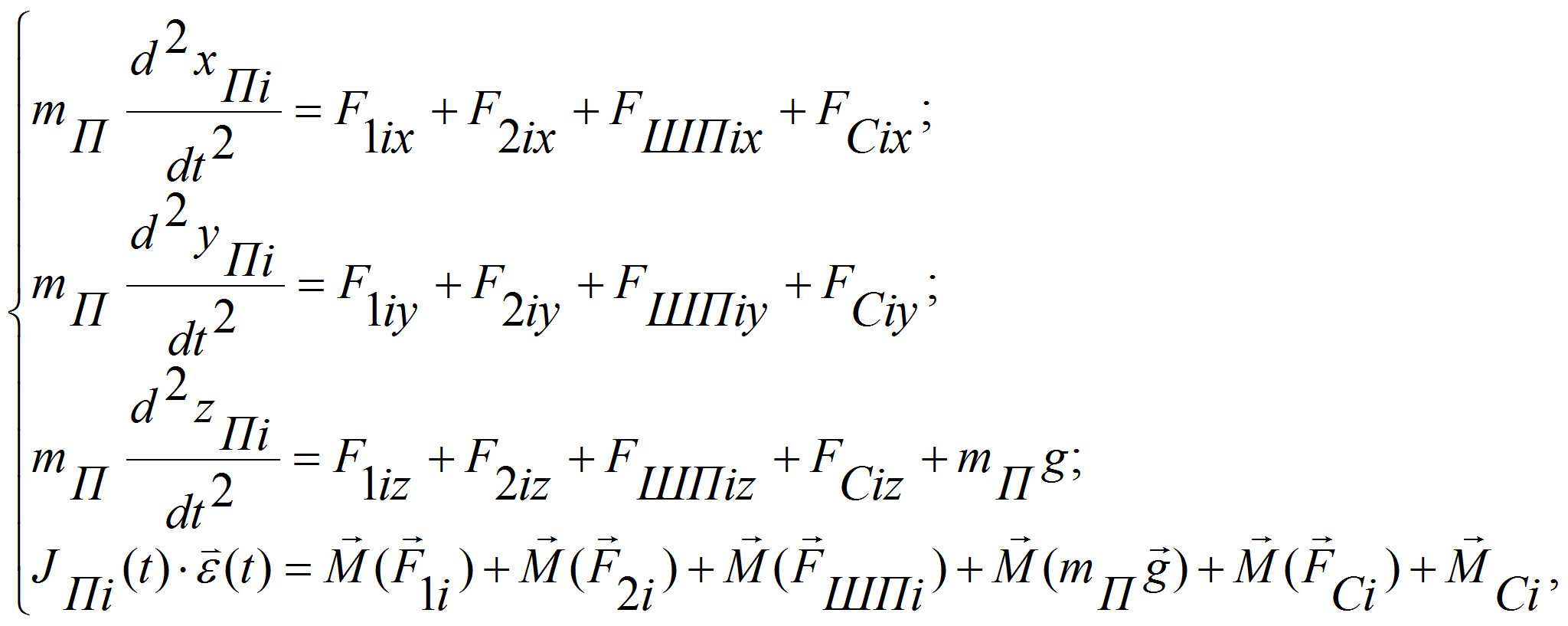В лесном хозяйстве широко применяются орудия различного назначения, рабочие органы которых взаимодействуют с почвой. Наибольший интерес представляют рабочие органы, вращающиеся принудительно от ВОМ трактора и деформирующие почву с целью улучшения аэрации и уничтожения сорняков. При этом рабочие органы одновременно совершают поступательное и вращательное движение, т.е. имеет место механизм сложного взаимодействия с почвой. В наиболее общем случае такое взаимодействие рассматривается как:
где Р – оператор, характеризующий действие рабочих органов машины; Х1 и X2 – начальное и конечное состояние среды соответственно.
Воздействие внешней среды (допуски поверхностных неровностей) Sg (Ω) и реакции орудия Sv (Ω) связывают с помощью передаточной функции H (ω) так, что
где ω – угловая частота, ω = v·Ω; v – скорость орудия.
- Передаточная функция Н (ω) определяется аналитически, или изменением входного и выходного спектров амплитуд, скоростей, ускорений, сил и т. д. Так, Sg (Ω) является мерой энергетического спектра ускорений, возникающих из-за поверхностных неровностей.
Реальное орудие значительно отличается от такой модели, что осложняет использование передаточных функций для анализа динамики орудия. Схему машины можно представить как систему сосредоточенных масс [1, 2], соединенных упругими звеньями или распределенных в пределах определенных участков. Приведенные массы могут быть по величине постоянными или переменными. Жесткость упругих звеньев и внешние силы в общем случае являются переменными, зависящими от положения системы или скорости ведущего элемента. Иногда внешние силы выражаются в функции времени.
Для решения задач динамики схемы исследуемых механизмов удобно представить в виде отдельных элементов, соединенных между собой упругими связями.
При распределенных массах рассмотрение динамики упругих систем сводится к решению так называемых волновых уравнений типа:
где u – среднее смещение элемента среды; a – фазовая скорость.
Жесткие системы могут быть представлены в виде одной приведенной массы (момента энергии), движущейся под действием приведенной силы (момента).
Среда в общем виде записывается системой дифференциальных уравнений в частных производных:
где θi – функция, описывающая состояние среды; Fij (xi, t) – внешние силы; aik, bik, Aij, Bij, Cij – параметры, зависящие от свойств среды. Однако в зависимости от воздействия классы этих уравнений различны.
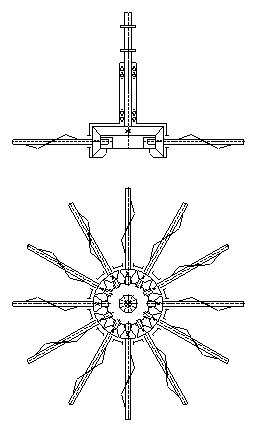
Рассмотрим с данной позиции роторный рабочий орган (рис. 1), выполненный в виде установленной на наклонной оси свободно вращающейся звездочки с радиально расположенными пальцами [3].
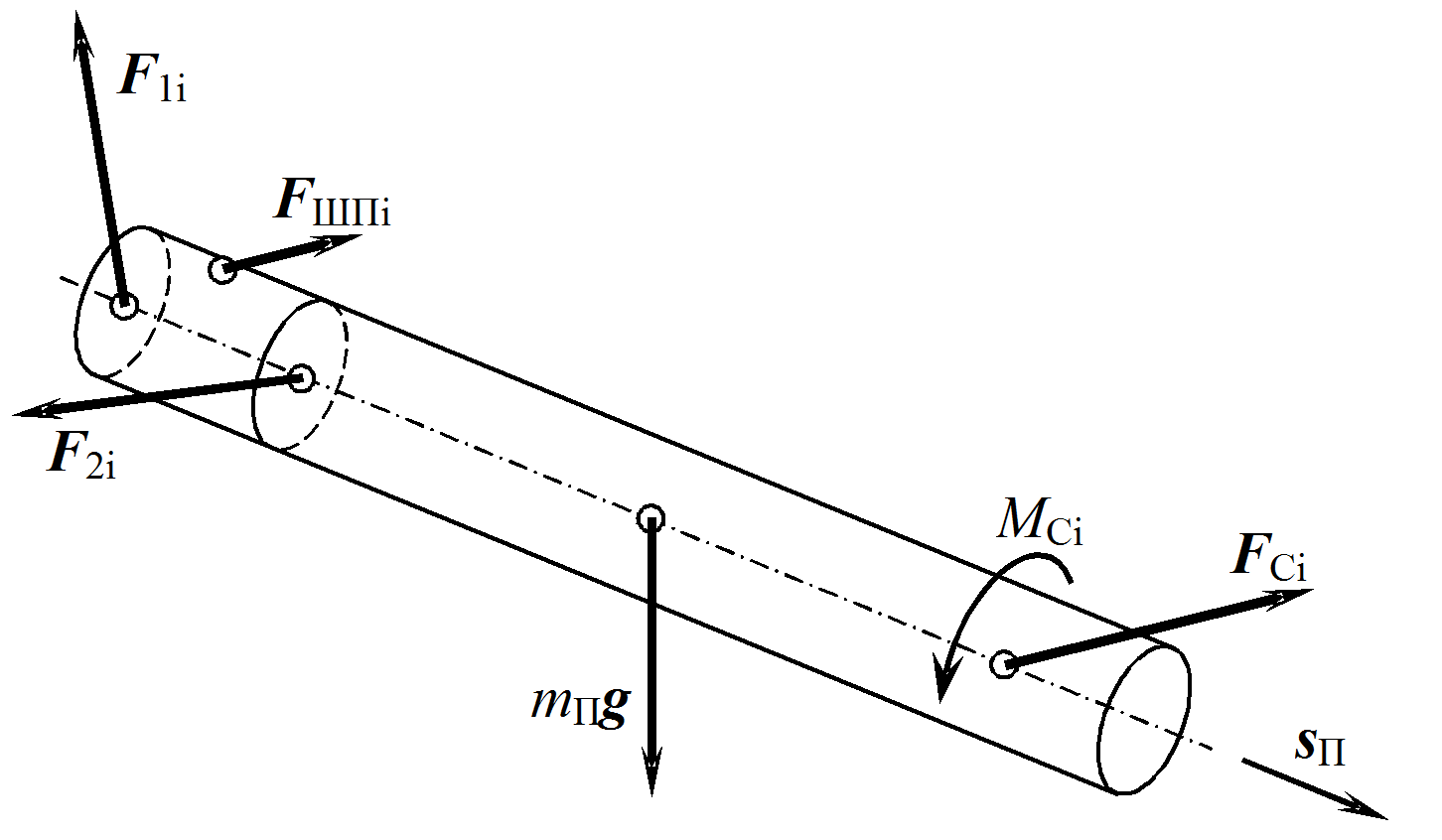
Каждый палец в процессе работы механизма совершает сложное движение - как вращательное, так и поступательное и испытывает действие сил со стороны деформируемой почвы, силы тяжести и реакции подшипников (рис. 2).
Рис. 1. Принципиальная схема конструкции роторного рабочего органа культиватора для ухода в рядах лесных культур
Рис. 2. Расчетная схема к составлению уравнений движения пальца
Тогда уравнения движения пальца i записываются следующим образом:
где mП – масса пальца; F1ix, F1iy, F1iz – декартовы составляющие силы в первом подшипнике; F2ix, F2iy, F2iz – декартовы составляющие силы во втором подшипнике; FШПix, FШПiy, FШПiz – декартовы составляющие силы взаимодействия с ведомой шестерней; FСix, FСiy, FСiz и MCi – декартовы составляющие силы и момент сопротивления со стороны почвы; mПg – сила тяжести.
Каждый палец вращается в двух подшипниках, которые в свою очередь установлены в корпусе. Каждый подшипник в модели заменяется парой точек: одна точка на корпусе, другая на пальце. Обозначим точки на корпусе как K1i и K2i, а точки на i-пальце P1i и P2i на пальце. При смещении точки Pj относительно соответствующей точки Kj в подшипниках возникают силы, стремящиеся снова совместить точки Pj и Kj. Так как по природе это силы упругого взаимодействия стальных элементов подшипников, возникающие силы в модели учитываются следующим образом:
где CП и DП – коэффициент упругости и коэффициент демпфирования; xK1i, yK1i, zK1i – координаты точки K1i; xP1i, yP1i, zP1i – координаты точки P1i.
При вращении корпуса координаты точек K1i и K2i постоянно изменяются. В модели координаты указанных точек, соответствующие текущему значению угла поворота корпуса φК рассчитываются следующим образом.
Во-первых, точки-подшипники распределяются равномерно по окружности корпуса:
где i – индекс подшипника.
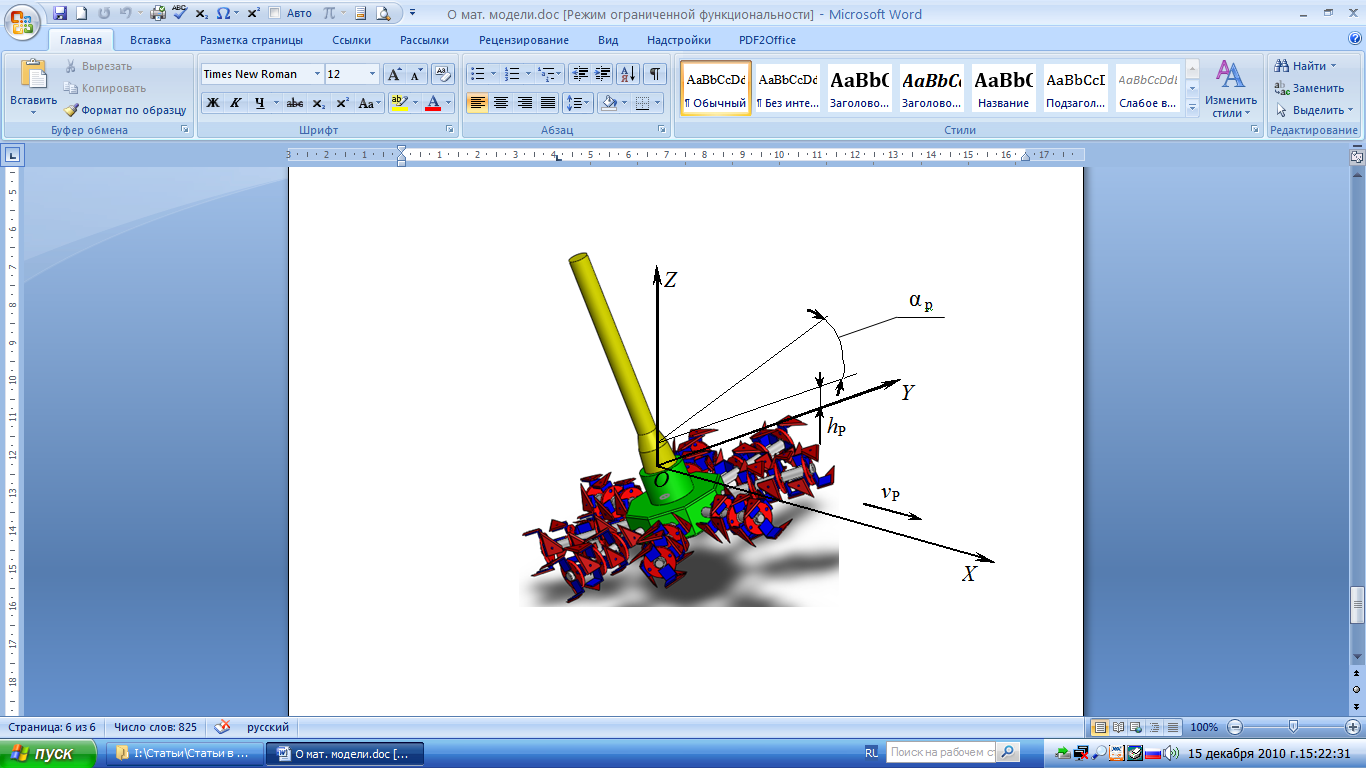
Во-вторых, необходимо учесть, что ротор установлен под углом αР к поверхности почвы (рис. 3). Для этого координаты пересчитываются следующим образом:
И, наконец, производится перемещение рабочего органа в горизонтальном направлении на расстояние vРt и в вертикальном – на расстояние hР:
Рис. 3. Расположение системы координат по отношению к моделируемому механизму
Координаты точек P1i и P2i зависят от положения и угла поворота пальца и в процессе численного интегрирования подлежат постоянному пересчету.
Таким образом, мы перешли от наиболее общих уравнение (1 – 4) к установлению соотношений функциональной связи исполнительной части культиватора с внешней средой, что позволяет представить данные зависимости в виде алгоритма для ЭВМ и провести численный эксперимент, описывающий процесс рыхления почвы.
- Литература:
1. Бутковский А.Г., Пустыльников Л.М. Теория подвижного управления системами с распределенными параметрами. М.: Наука,1080. 383 с.
2. Длоугий В.В., Клауз Л.П. К теории виброуплотнительных машин. – В кн.: Республиканский межведомств. научно-техн. сб. Сер. Теория механизмов и машин, вып. 33, Харьков, 1982, с. 9-16.
3. А. с. 380256 СССР, МКИ A 01 В 35/16, A 01 В 39/16. Ротационный рабочий орган культиватора-рыхлителя / И. М. Бартенев [и др.]; И. М. Бартенев, В. В. Попов, Ю. М. Жданов, В. Л. Аравийский; заявитель и патентообладатель: ВНИАЛМИ. – № 1702643; заявл. 04.10.1971; опубл. 15.05.73, Бюл. № 21. – 2 с.