Математическая модель активного взаимодействия может быть получена на основе рассмотрения двух возможных перемещений или воздействий элементов рабочих органов на материал: касательного и нормального к поверхности липкой породы. В зависимости от угла воздействия или заострения рабочего органа каждая схема может быть двух видов, которые отличаются наличием или отсутствием уплотненного ядра, дополняющего рабочий орган.
Влияние скорости перемещения для любой схемы взаимодействия на возникающие сопротивления проявляется по поверхностям скольжения и рабочего органа. Этот показатель учитывают так же, как и при пассивном взаимодействии, коэффициентом влияния скорости [1,2].
Для модели активного взаимодействия может быть принят за основу метод поэлементного расчета сопротивлений [3]. При этом необходимо принять следующие допущения: призмы материала, ограниченные плоскостями скольжения, при взаимодействии не подвергаются уплотнению, а являются как бы «затвердевшими телами»; плоскости скольжения имеют прямую форму и выходят на свободную поверхность под углом, равным 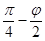 , где
, где 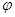 -угол внутреннего трения липкой породы.
-угол внутреннего трения липкой породы.
Рассмотрим общий случай нормального воздействия рабочего органа на поверхность материала (см. рисунок 1), когда уплотненное ядро дополняет рабочий орган. Проанализируем последовательно условия равновесия призм материала, ограниченных плоскостями скольжения.
Для призмы материала сечением bdec:
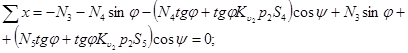
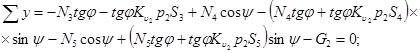 (1)
(1)
сечением 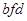
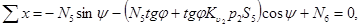
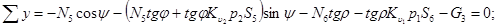 (2)
(2)
сечением 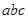
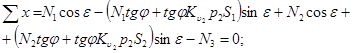
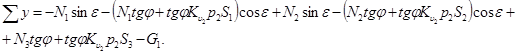 (3)
(3)
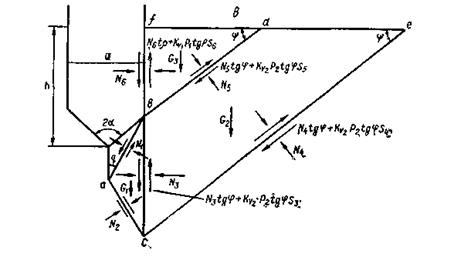
Рисунок 1 – Физическая модель активного взаимодействия при нормальном воздействии рабочего органа на массив породы
Значения 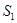 ,
, 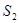 ,….,
,…., 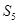 ,
, 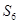 ,
, 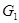 ,
, 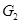 и
и 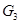 при глубине внедрения h, толщине рабочего органа а,ширине b с углом заострения
при глубине внедрения h, толщине рабочего органа а,ширине b с углом заострения 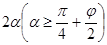 составляют:
составляют:
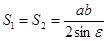 ; (4)
; (4)
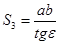 ; (5)
; (5)
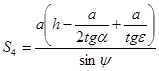 ; (6)
; (6)
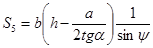 ; (7)
; (7)
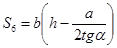 ; (8)
; (8)
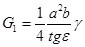 ; (9)
; (9)
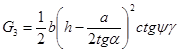 ; (10)
; (10)
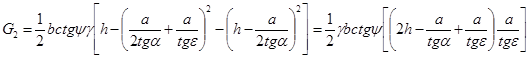 . (11)
. (11)
Применив тригонометрические преобразования, преобразуем выражения (1) - (3) и получим алгебраическую систему уравнений, линейную относительно неизвестных 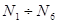 вида
вида
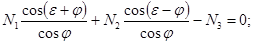
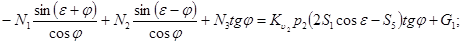 (12)
(12)
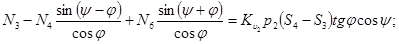
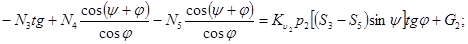
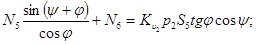
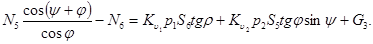
Эту систему можно разделить на три подсистемы: I – 1 и 2 уравнения, II – 3 и 4, III – 5 и 6. Решим подсистему III, найдем значение силы 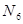 . Для этого первое ее уравнение умножим на
. Для этого первое ее уравнение умножим на 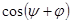 и, почленно сложив со вторыми умножив на
и, почленно сложив со вторыми умножив на 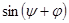 , получим
, получим
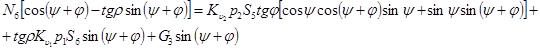 (13)
(13)
или
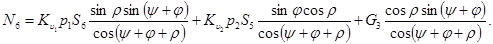 (14)
(14)
Из подсистемы II определим значение силы 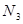 . Умножим первое уравнение системы на
. Умножим первое уравнение системы на 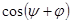 , а второе – на
, а второе – на 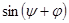 и, почленно сложив, найдем
и, почленно сложив, найдем
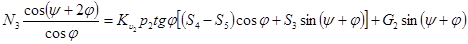 (15)
(15)
или
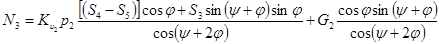 . (16)
. (16)
Из системы I определим значение силы 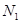 . Умножим первое ее уравнение на
. Умножим первое ее уравнение на 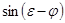 , а второе – на -
, а второе – на -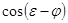 и, почленно сложив, найдем
и, почленно сложив, найдем
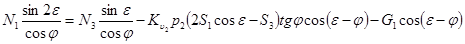 (17)
(17)
или
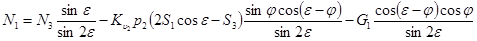 . (18)
. (18)
Подставив выражение (16) из (14), вычислим
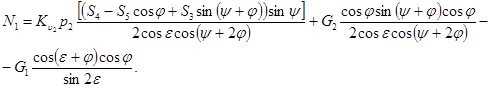 (19)
(19)
Усилие, необходимое для внедрения рабочего органа в массив липкой породы, определим по формуле
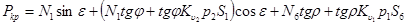 (20)
(20)
или
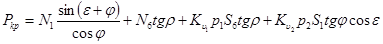 . (21)
. (21)
Подставляя в (21) значения сил 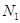 и
и 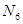 получим:
получим:
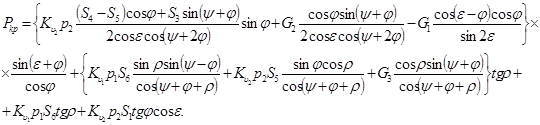 (22)
(22)
Сделав приведение подобных членов и внеся соответствующие обозначения, найдем:
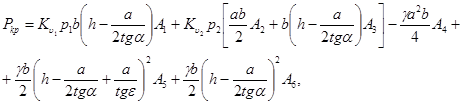 (23)
(23)
где
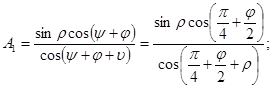 (24)
(24)
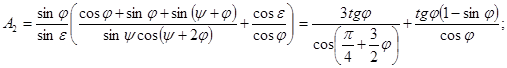 (25)
(25)
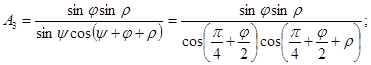 (26)
(26)
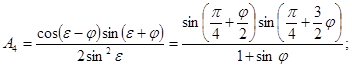 (27)
(27)
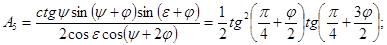 (28)
(28)
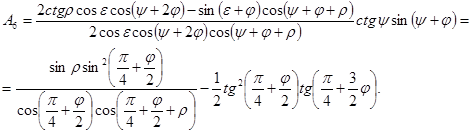 (29)
(29)
Таким образом, процессы взаимодействия рабочих органов добывающих машин с липкими породами представляют собой совокупность или сочетание элементарных взаимодействий - активного (рабочего органа на среду) и пассивного (среды на рабочий орган), каждое из которых может происходить при относительном перемещении или без такового. Коэффициенты рассчитываем в зависимости от соотношения 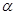 и
и 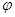 по формулам, полученным по той или иной схеме. В результате можно найти коэффициенты при нормальном воздействии на массив породы.
по формулам, полученным по той или иной схеме. В результате можно найти коэффициенты при нормальном воздействии на массив породы.
Литература
1. Баловнев В.И. Моделирование процессов взаимодействия со средой рабочих органов дорожно-строительных машин. М., 1981. 335 c.
2. Ветров Ю.А., Кархов А.А., Кондра А.С., Станевский В.П. Машины для земляных работ. Киев, 1981. 383 с.
3. Заднепровский Р.П. Результаты снижения трения и прилипания влажных грунтов при разработке землеройными машинами//Строительные и дорожные машины. 1973. №5. C. 31-33

