Уменьшение затрат времени на криптографические преобразования при реализации блочных шифров является оптимальной задачей защиты информации, поскольку использование таких преобразований не должно снижать производительность компьютерных систем и сетей. Для решения данной задачи предложены множество специальных способов шифрования [1], основанные на применении перестановок, подстановок, логических преобразований и арифметических операций. Комбинирование перестановок, подстановок и логических преобразований позволяет значительно расширить класс возможных недорогих микроэлектронных шифрирующих устройств, обеспечивающих скорость шифрации до 1 Гб бит/сек. Эти способы шифрования ориентированы на использование в составе комбинированных криптографических систем с целью повышения криптостойкости их при минимальных временных затратах.
В данной статье предлагается специальный способ шифрования и структура специализированного вычислительного устройства для его реализации.
Данный способ шифрования основывается на математических операциях над матрицами, т. е. на операциях умножения вектора на матрицу (DМ=В при шифрации и BМ-1=D при дешифровании) [2].
Рассмотрим алгоритм шифрования данных согласно выражениюDМ=В.
Пусть, заданы четырехмерный вектор D, и четырехмерная квадратная матрица Мij. Требуется определить четырехмерный вектор В.
ВыраженияDМ=В можно представить в следующем виде:
![]()
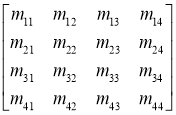 =
=![]() ,
,
где: b1=d1m11+d2m12+d3m13+d4m14; b2=d1m21+d2m22+d3m23+d4m24;
b3=d1m31+d2m32+d3m33+d4m34; b4=d1m41+d2m42+d3m43+d4m44.
Для реализации обратного процесса, т. е. для дешифрования или восстановления D необходимо определить обратную матрицу М-1. Определение исходного вектора D реализуется согласно с выражением:
BМ-1=D,
или
![]()
 =
=![]() .
.
Здесь d1, d2, d3 и d4 соответственно равны:
d1=b1 ![]() 11+b2
11+b2 ![]() 12+b3
12+b3 ![]() 13+b4
13+b4 ![]() 14; d2=b1
14; d2=b1 ![]() 21+b2
21+b2 ![]() 22+b3
22+b3 ![]() 23+b4
23+b4 ![]() 24;
24;
d3=b1 ![]() 31+b2
31+b2 ![]() 32+b3
32+b3 ![]() 33+b4
33+b4 ![]() 34; d4=b1
34; d4=b1 ![]() 41+b2
41+b2 ![]() 42+b3
42+b3 ![]() 43+b4
43+b4 ![]() 44;.
44;.
Единственным условием выполнения обратности процесса является неравенство нулю элементов матриц ![]() .
.
Для шифрования исходный текст разбивается на векторы (В) длиной один байт и каждый вектор перемножается на квадратную матрицу (![]() ). Каждый вектор шифрируется независимо от других, поэтому можно осуществить передачу блоков данных и произвольный доступ к запрограммированным данным.
). Каждый вектор шифрируется независимо от других, поэтому можно осуществить передачу блоков данных и произвольный доступ к запрограммированным данным.
Достоинством данного способа является его гибкость при реализации и использовании в различных приложениях обработки информации.
Предложенный способ может быть реализован аппаратно и программно, но предпочтение отдается аппаратной, т. к. высокая оперативность выполнения шифрования обеспечивается при аппаратной реализации [3].
Рассмотрим вкратце структурную схему устройства шифрования данных с использованием операций над матрицами (Рис.1).
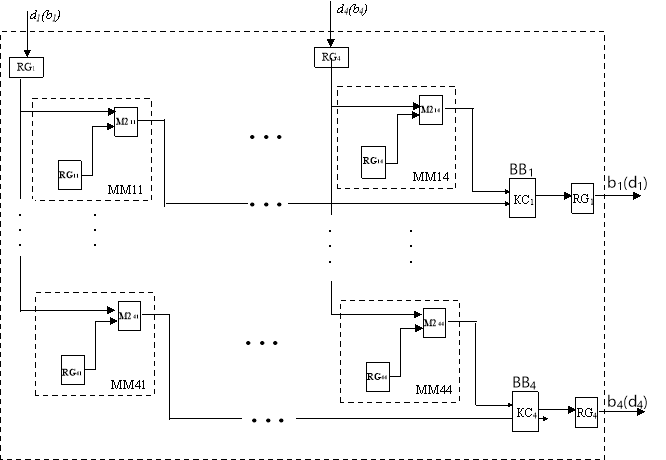
Рис. 1. Структурная схема устройства криптации с использованием операций над матрицами.
Устройство выполняет операцию перемножения матрицы М (обратной матрицы М-1) на вектор D(В) и состоит из четырех 8-разрядных RG1,...,RG4, четырех векторов-вычислителей ВВ1,...,ВВ4. Каждый вектор-вычислитель состоит из четырехвходового комбинационного сумматора KCi, второго 8-разрядного регистра и множительных модулей MMi1,...,MMi4. Каждый множительный модуль MMij(j=1,..,4) состоит из третьего 8-разрядного регистра RGij и множителя Mij.
Как шифрование, так и дешифрование данных в устройстве осуществляется в 4 этапа.
Для дешифрования данных в буферные регистры RGj вводятся значение вектора В, а в регистры RGij соответствующие элементы обратной матрицы М-1.
Первый этап. Значение вектора D (В) вводится через буферные регистры RGj, а значения матрицы М через регистры памяти RGij.
Второй этап. Выполняются операции умножения значения векторов с элементами матрицы в множительных модулях ММij.
Третий этап. Полученные результаты (т. е. произведения) в модулях умножения ММij суммируются в соответствующих комбинационных сумматорах KCj.
Четвертый этап. Вычисленные значения (т. е. значение вектора В (D)) на выходах сумматоров KCj передаются на сдвигающий регистр RG.
Предложенные в работе специальный способ и аппаратное средство шифрования информации в компьютерных сетях, позволяют организовать системы защиты информации, отличающиеся высоким быстродействием и простой реализацией.
Литература:
- В. Ф. Шаньгин. Информационная безопасность компьютерных систем и сетей: Учебное пособие — М.: ИД ФОРУМ: НИЦ ИНФРА — М, 2014 г. — С.416.
- Каримов М. М. Применение аппаратных средств защиты информации в компьютерных сетях / Сбор.научн.трудов ИПМЭ НАН Украины.Киев,2001,вып.9.- С. 8–14
- Платонов В. В. Программно-аппаратные средства защиты информации: учебник для студ. учреждений высш. проф. Образования /
- В. В.Платонов. М.: Издательский центр «Академия», 2013 г. С.336.

