Моделирование — это, в широком смысле, один из способов познания реальности. Оно включает в себя анализ определенного объекта реального мира и перенос его изучаемых свойств на модель — систему, служащую для представления реального процесса или устройства.
Математическая модель создается с помощью языка математики, то есть различных графиков, функций, таблиц, графов и др.
Современные технологии позволяют создавать различные математические модели в короткие сроки и быстро изучать требуемые данные, которые можно использовать для производства каких-либо изделий.
В машиностроении широко используются, например, средства автоматизированного проектирования, языки программирования и другое программное обеспечения для математических расчетов и визуального представления изделий для изучения их статических, динамических, геометрических характеристик. Но для того, чтобы вычислительной техникой тем или иным образом воспринимались входные данные нужно создать математическую модель исследуемого объекта.
Продемонстрируем каким образом может выглядеть математическая модель объекта, который касается конструкции наземно-транспортных комплексов. Например, рассмотрим землеройную машину — экскаватор и обратим внимание на его рабочий орган — ковш (рисунок 1).
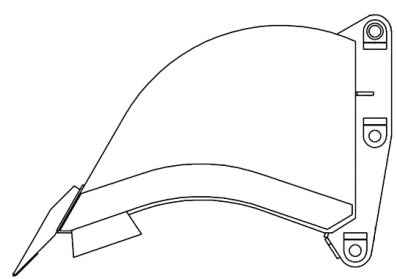
Рис. 1. Ковш экскаватора
В первом приближении можно математически задать контур ковша с помощью функций: линейной и квадратного трехчлена. Это поможет нам рассчитать некоторые технические характеристики ковша для его дальнейшего проектирования. Методика расчета взята из источника 1.
Вместимость ковша можно определить по формуле:
![]() (1)
(1)
где ![]() — средняя ширина ковша;
— средняя ширина ковша; ![]() — площадь осевого сечения.
— площадь осевого сечения.
Площадь осевого сечения (рисунок 2) определяется по следующей формуле:
![]() (2)
(2)
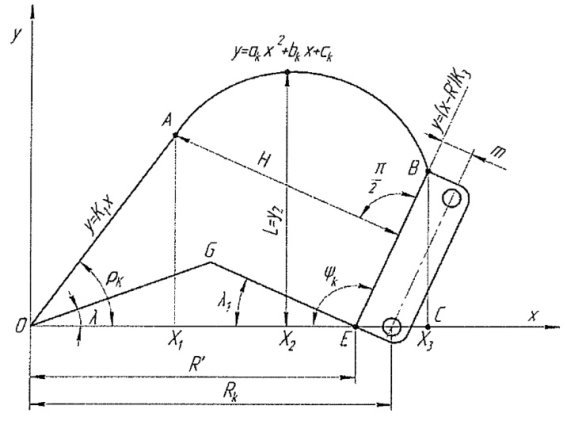
Рис. 2. Осевое сечение ковша
Раскрывая значения составляющих уравнения (2) и подставляя его в уравнение (1), получим:
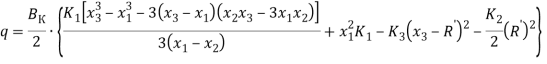 (3)
(3)
где
![]() (4)
(4)
![]() (5)
(5)
Контур поперечного сечения ковша описывается выражениями:
участок OA:![]() (6)
(6)
участок AB:![]() (7)
(7)
участок BE: ![]() (8)
(8)
где
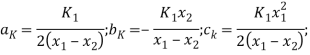 (9)
(9)
Совместное решение уравнений (7) и (8) позволяет найти абсциссу точки B как
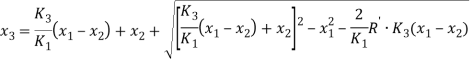 (10)
(10)
Соотношение между высотой ковша ![]() и его глубиной
и его глубиной ![]() может быть представлено в виде
может быть представлено в виде
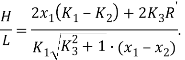 (11)
(11)
Совместное решение уравнений (3), (10) и (11) для заданных
![]() позволяет найти
позволяет найти ![]()
Параметры ![]() зададут необходимый объем ковша, который будет требоваться в процессе проведения работ. Расстояния
зададут необходимый объем ковша, который будет требоваться в процессе проведения работ. Расстояния ![]() и соотношение
и соотношение![]() определят габаритные размеры, которыми должен обладать ковш. Углами
определят габаритные размеры, которыми должен обладать ковш. Углами ![]() задается положение стенок относительно обрабатываемой поверхности. Данные параметры будут предусматриваться техническим заданием для проектирования конструкции ковша и с помощью них мы сможем найти расстояния от крайней точки зубьев до стенки с элементами крепления.
задается положение стенок относительно обрабатываемой поверхности. Данные параметры будут предусматриваться техническим заданием для проектирования конструкции ковша и с помощью них мы сможем найти расстояния от крайней точки зубьев до стенки с элементами крепления.
Все заданные параметры могут быть проанализированы с помощью средств программного обеспечения. Таким образом, можно сказать, что математическое моделирование является вспомогательным инструментом для создания компьютерных моделей и проведения вычислений с помощью языков программирования, что существенно ускоряет процессы проектирования и конструирования различных механизмов, деталей агрегатов и др.
Литература:
- Шемякин С. А., А. В. Лещинский. Расчет землеройных машин. — Хабаровск: Изд-во Тихоокеан. гос. ун-та, 2014. — 55 с.

