В данной работе рассматривается применение аппроксимационных алгоритмов с гарантированной оценкой точности к задаче составления расписания на одном процессоре, где каждая работа имеет время выпуска, время обработки и время доставки.
Ключевые слова: расширенное правило Джексона, аппроксимационные алгоритмы, гарантированная оценка точности, интерференционная работа
Рассмотрим следующую задачу планирования: n работ должны быть выполнены на одной машине без прерываний. Каждая i-я работа имеет:
‒ ri — время поступления работы, до которого работа не может быть поставлена на выполнение;
‒ pi — время выполнения работы на машине;
‒ qi — время доставки. Процесс доставки начинается сразу после того, как работа выполнена.
Через π будем обозначать перестановку из n элементов, задающую последовательность работ на машине.
Задача: минимизировать значение целевой функции
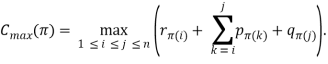
Определение 1. Перестановка π*, минимизирующая Cmax(π) среди всех перестановок π из n элементов, называется оптимальной.
В связи с тем, что построение точных и эффективных алгоритмов проблематично для рассматриваемой задачи, актуальным становится построение и анализ приближенных алгоритмов с гарантированной оценкой точности.
Определение 2. Оценкой точности некоторого алгоритма A будем называть отношение:
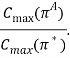
Определение 3. Говорят, что алгоритм имеет гарантированную оценку точностиconst, если
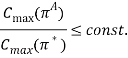
Определение 4. Путем (i, j) в перестановке π называется последовательность работ 
, где 1 ≤ i ≤ j ≤ n.
Определение 5. Путь (a, b), для которого
называется критическим путем в перестановке π.
Рассмотрим пример задачи, в которой количество работ n = 7.
Пример 1. Задача с количеством работ, равным 7:
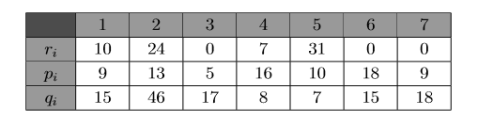
Рассмотрим некоторую перестановку π. Путь (1, 5) будет являться критическим.
Определение 6. Пусть (a, b) — критический путь перестановки π. Такая работа с, что
где 
называется интерференционной работой.
Пример 2. Интерференционной работой для примера 1 будет являться работа 6.
Базовым подходом к рассматриваемой задаче является алгоритм, разработанный Schrage (см. [4]), называемый расширенным правилом Джексона.
Расширенное правило Джексона: Всякий раз, когда машина свободна, и одна или более работ доступны для выполнения, выбирается работа с наибольшим временем доставки.
Для введенной ранее задачи (см. пример 1) рассмотрим перестановку 
, полученную с помощью описанного правила.
Пример 3. Перестановка для примера 1.
Теорема 1 (Kise, см. [2]). Пусть — перестановка, полученная по расширенному правилу Джексона. Тогда оценка точности значения целевой функции:
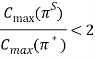
Для рассматриваемой задачи E.Nowicki и C.Smutnicki представили более эффективный алгоритм [1], который в отличии от алгоритма Schrage имеет гарантированную оценку точности 3/2 и вычислительную сложность порядка O(nlogn). Данный алгоритм, называемый алгоритмом H, использует в качестве базовой перестановку, полученную с использованием расширенного правила Джексона. Вычисление состоит из трех основных шагов.
Шаг 1: Используя расширенное правило Джексона, находим начальную перестановку и интерференционную работу 
. Если такая работа c не найдена, то заканчиваем вычисления и полагаем
Шаг 2: Находим
‒ 
,
‒
,
‒ перестановку 
такую, что 
в не убывают,
‒ перестановку 
такую, что 
в 
не убывают,
Положим
Шаг 3: Находим 
такую что
Рассмотрим работу алгоритма на примере 1.
Пример 4. На первом шаге воспользуемся расширенным правилом Джексона и получим перестановку :
Путь (1,5) будет являться критическим, а работа 6 — интерференционной. Далее найдем множества A и B, а также соответствующие им перестановки:
Положим 
:
Таким образом, в качестве ответа алгоритма будет выбрана перестановка 
.
Теорема 2 (Lenstra, см. [3]). Пусть 
— перестановка, полученная алгоритмом H. Тогда значение целевой функции оценивается неравенством:
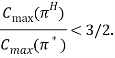
Таким образом, в данной работе представлены основные аппроксимационные алгоритмы с гарантированной оценкой точности для задачи теории расписаний с временами поступлений и временами доставки.
Литература:
- Nowicki E., Smutnicki C. An approximation algorithm for a single-machine scheduling problem with release times and delivery times // /Discrete Applied Mathematics. —: North-Holland, 1994. — С. 69–79.
- Kise H., Ibaraki H.. Performance analysis of six approximation algorithms for the one-machine maximum lateness scheduling problem with ready times // J. Oper. Res. Sot. Japan. — 1979. — № 22. — С. 205–244.
- Lenstra J. K. Sequencing by enumerative methods // Mathematical Centre Tracts. — 1977. — № 69. — С. 128–141.
- Schrage L. Obtaining optimal solution to resource constrained network scheduling problem // Unpublished manuscript. — 1971.
