В статье представлена модель эпидемического процесса с последующим исследованием соотношения времени и интенсивности вакцинации для предотвращения вспышки заболеваемости.
С помощью математической модели исследуется проблема поддержания коллективного иммунитета, обеспечивающего сдерживание вспышки заболеваемости.
Задачи практической эпидемиологии связаны с отысканием необходимых уровней коллективного иммунитета, обеспечивающих сдерживание эпидемического процесса в пределах, определяемых эпидемическим порогом. Это осуществляется путём вакцинации, обеспечивающей получение нужного уровня коллективного иммунитета.
Для расчёта граничных параметров вакцинации можно использовать математическое моделирование динамики групп населения с помощью систем дифференциальных уравнений. Используя и модифицируя уже существующие модели, описывающие естественное развитие эпидемий, можно сделать выводы о характеристиках необходимого управления. Цель статьи — описать метод получения границы области с допустимыми параметрами вакцинации при реализации модели эпидемии в прикладном пакете Simulink
Постановка задачи
Для описания динамики развития эпидемического процесса в группе воспользуемся классической моделью Кермака-Кендрика [1], дополнив её управляющим воздействием в виде активной вакцинации. Она вызывает у восприимчивых иммунный ответ организма – формирование антител, занимающее некоторое время TV. В результате вакцинированные становятся иммунными.
Пусть S – число восприимчивых в группе детей, I — число инфицированных, Iv — число вакцинированных, R — число иммунных; u — интенсивность вакцинации в группе детей, λ — заболеваемость (человек в сутки).
Тогда развитие управляемого эпидемического процесса описывается следующей системой дифференциальных уравнений:
(1)
Будем полагать, что вакцинация начинается в момент T0 = 0 и длится не более Tm дней. Развитие эпидемического процесса будем прослеживать на протяжении TE дней. Требуется построить кривую 
— границу области допустимых управлений, то есть области, в которой
(2)
Метод решения.
Для решения построим модель нашей системы (1) в пакете Simulink (рис. 2). Каждому конкретному значению u = uk ищем такую длительность вакцинации TP ≤ Tm, что заболеваемость λ не превосходит пороговой 
. Или, наоборот, для интересующих нас значений продолжительности T = TP ≤ Tm периода вакцинации находим интенсивность, обеспечивающую выполнение неравенства (2). По полученным точкам строим кривую.
Пример
Так как вакцинация длится на протяжении не более трёх осенних месяцев, то в качестве Tm берем 100 дней. Будем полагать, что эпидемия заканчивается в конце марта: TE = 200 дней.
Пусть в некотором крупном городе имеется 1 миллион восприимчивых человек: S0 = 1000. А 900 человек (I0 = 0.9) инфицированы некоторым вирусом с характерным временем болезни Ti = 10 дней. Предположим также, что против данного вируса существует вакцина, которая дает иммунитет примерно через две недели (TV = 15). Определим коэффициенты нашей системы:
(3)
Возьмем
. Применяя описанную методику к данному примеру получим решение поставленной задачи в следующем виде.
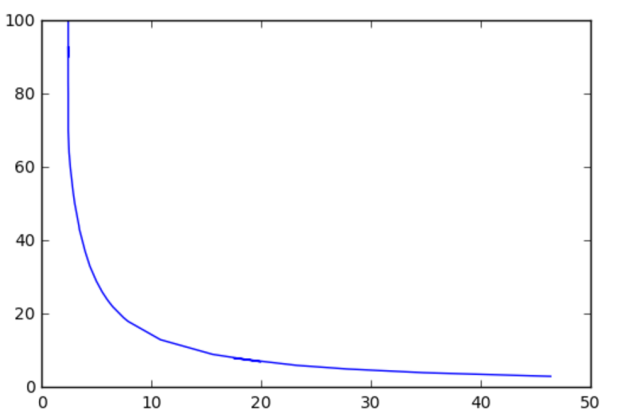
Рис. 1. По оси абсцисс — u, по оси ординат — Т
Обсуждение
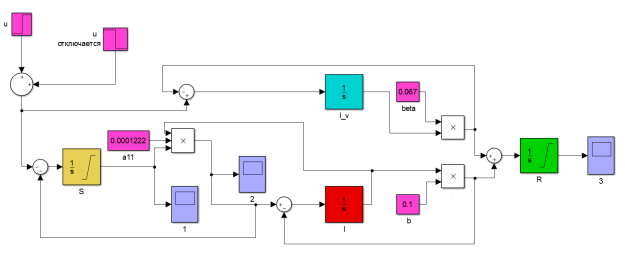
Рис. 2.
Визуальное представление модели в системе Simulink облегчает восприятие механики взаимодействия групп населения. Кроме того, модель крайне проста и легко модифицируема. Константы a, b и β, начальные условия, продолжительность и интенсивность вакцинации — все это можно изменить, открыв соответствующие блоки.
В блоке «2» строится график заболеваемости в течении всего периода эпидемии. А блоки «1» и «3» нужны для проверки корректности работы алгоритма.
В ходе исследования было обнаружено, что в условиях рассматриваемого примера при вакцинации с параметрами u = 138.7, Т = 1 (то есть за один день) заболеваемость не превзойдет пороговой.
Заключение
Построенная модель позволила исследовать соотношение двух параметров вакцинации — её интенсивности и длительности, — обеспечивающее сдерживание эпидемической вспышки, то есть поддержание заболеваемости на уровне, не превышающем эпидемический порог.
Литература:
- Колесин И. Д., Житкова Е. М. Математические модели эпидемий. — СПб.: СОЛО, 2017.
- Смирнов Н. В., Смирнов М. Н., Смирнова М. А. Решение прикладных задач теории управления в MATLAB. — СПб.: СОЛО, 2013.
