В работе рассматривается основные методы группировки данных при «обучении без учителя» (самообучении), т. е. в условии, когда имеется непомеченная выборка.
Ключевые слова: распознавание образов, алгоритмы группировки, алгоритм минимума, алгоритм максимума
Решающее правило в распознавании образов — это алгоритм, который позволяет по результатам измерений определенных признаков объекта принять решение о значениях необходимых нам параметров этого объекта.
Задача построения решающего правила в условиях полной апостериорной неопределенности достаточно проблематична. В таком случае имеется множество выборочных значений (представленных, например, в виде файлов данных наблюдений) без указания их классификации. Таким образом, изначально не известно, что это за объекты (рисунок 1).
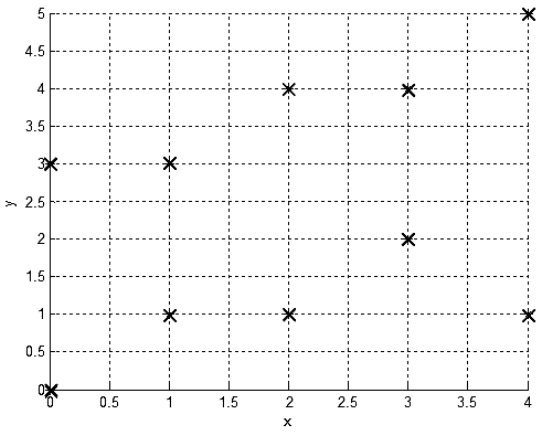
Рис. 1. Исходные данные
Поэтому первым шагом для «самообучения» сети необходимо разделить данные на подгруппы. Данные с похожими признаками заносятся в одну группу. Возникает вопрос: как измерить сходство между наблюдениями (точками)? Самый простой способ — измерение расстояния между наблюдениями. В одном классе расстояние между отсчетами будет существенно меньше, чем расстояние между точками из разных классов.
Алгоритм «ближайшего соседа»
Алгоритм «ближайшего соседа» часто называют алгоритмом минимума. Суть алгоритма заключается в следующем: при классификации неизвестного объекта находится заданное число n геометрически ближайших к нему в пространстве признаков других объектов (т. е. ближайших соседей) с уже известной принадлежностью к распознаваемым классам (рисунок 2).
Итак, рассматриваем случай, когда используется dmin, т. е. минимальное расстояние между точками. Предположим, что точки данных рассматриваются как вершины графа, а ребра графа образуют путь между вершинами в одном подмножестве X. Ближайшие соседи определяют ближайшие подмножества, когда для измерения расстояния между подмножествами используется dmin. Слияние Xi и Xj соответствует добавлению ребра между двумя ближайшими вершинами в Xi и Xj. Результирующий граф никогда не будет иметь замкнутых контуров или цепей, потому что ребра, соединяющие точки подмножества, всегда проходят между различными классами. Можно сказать, что эта процедура генерирует дерево (из терминологии теории графов). Продолжаем процедуру до тех пор, пока все точки подмножеств не будут соединены. В результате получаем остов — обыкновенный граф (дерево) с путем от любой вершины к любой другой вершине в группе, но без циклов. При этом сумма длин ребер результирующего дерева не должна превышать сумм длин ребер для любого другого покрывающего дерева для данного множества выборочных данных. Таким образом, используя dmin в качестве меры расстояния, агломеративная (объединительная) процедура превращается в алгоритм для создания минимального покрывающего дерева. Минимальное остовное (покрывающее) дерево можно получить, добавляя самое короткое ребро между двумя другими ребрами (двумя ближайшими парами точек).
Если некоторые точки расположены так, что между исходными группами создается некоторый мост, то это приводит к объединению данных в одну большую продолговатую группу или несколько маленьких. Такой эффект мы можем наблюдать, когда результаты очень чувствительны к шуму или к небольшим изменениям в положении точек данных [1].
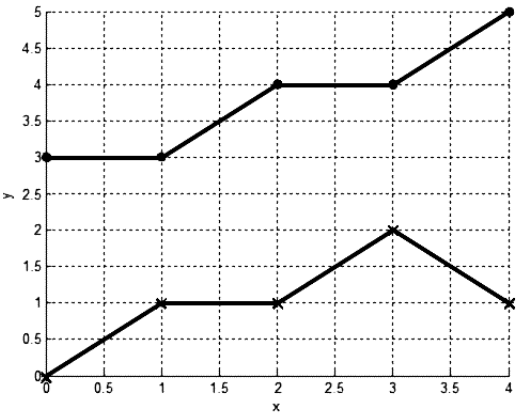
Рис. 2. Изображение результатов группировки данных алгоритмом ближайшего соседа
Алгоритм «дальнего соседа»
Метод «дальнего соседа» заключается в следующем: степень сходства оценивается между наиболее дальними наблюдениями (точками). Таким образом, при классификации неизвестного объекта находится заданное число n геометрически отдаленных от него в пространстве признаков других объектов (т. е. дальних соседей) (рисунок 3).
По аналогии с алгоритмом минимума алгоритм «дальнегососеда» называют алгоритмом максимума. Итак, рассматриваем случай, когда используется dmax, т. е. максимальное расстояние между точками. Применение алгоритма можно рассматривать как получение графа, в котором все вершины ребрами соединены в одну группу. Можно сказать, что каждая группа образует полный подграф (из терминологии теории графов). Расстояние между двумя группами определяется наиболее удаленными вершинами в обеих группах. Когда две ближайшие группы объединяются, в графе добавляются ребра между каждой парой вершин в обеих группах. Расстояние между двумя группами определяется наиболее удаленными вершинами в этих двух группах [1].
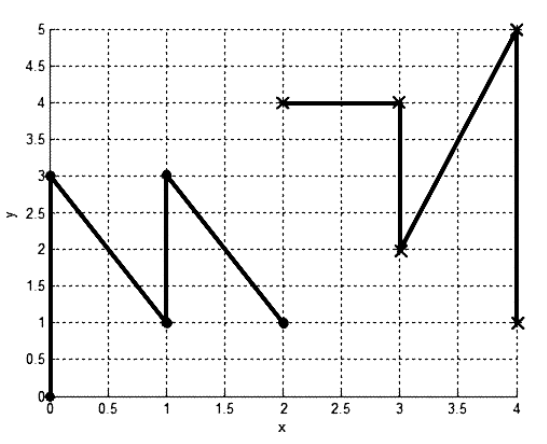
Рис. 3. Изображение результатов группировки данных алгоритмом дальнего соседа
Минимальный и максимальный алгоритмы представляют собой два крайних подхода в измерении расстояний между наблюдениями (точками). Таким образом, данные методы слишком чувствительны к различным отклонениям. Решить проблему поможет усреднение. Но оно требует замены расстояний на меры подобия, т. е. на безразмерный показатель сходства сравниваемых объектов.
Литература:
- Дуда Р., Харт П. Распознавание образов и анализ сцен: пер. с англ. / Р. Дуда, П. Харт; под ред. В. Л. Стефанюка — М.: Мир, 1976. — 512 с.
- Чистяков В. П. Курс теории вероятностей. — М.: Наука, 1987. — 224 с.

