При сопоставлении данных, собранных из различных источников, появляется сложность, связанная с возможными различиями формообразования в наименованиях и возникающих ошибках при ручном вводе данных. Были рассмотрены методы нечёткого сравнения строк.
Ключевые слова: алгоритмы, нечеткое сравнение, база данных, интеллектуальное сравнение.
Многие компании, занимающиеся деятельностью, связанной с оперированием большим числом различных данных, будь то сфера торговли, строительства или какая-либо другая, имеют необходимость в формировании некоторых справочных материалов, содержащих актуальную и архивную информацию о материалах, участвующих в технологическом процессе. В случаях, если компания имеет один централизованный источник данных, например, базы данных, эту операцию можно решить с помощью внутренних механизмов обработки данных. Однако в ситуации информация формируется из несколько различных типов источников, таких как базы данных, отчеты из информационных систем, архивные документы, в которых информация может быть представлена в различном формате. Также источники могут содержать синтаксические ошибки при ручном вводе, или иметь разный формат хранения из-за чего использование точного сравнения данных становится малоэффективным. Появляется необходимость применения нечетких методов обработки данных, содержащихся в источниках с последующей группировкой и консолидацией.
Данные, которые будут подвержены обработке, представляют собой кортеж полей, содержащий информацию характеризующий материал (код материала, краткое наименование материала, полное наименование и т. п.).
Данные для обработки хранятся в исторических выгрузках, которые поставляются из различных баз-поставщиков. Исходя из этого необходимо произвести обработку полученных данных, включающее исправление ошибок ввода, приведение данных к общему виду и формирования конечного файла, который в последствие будет загружен в единую базу данных.
Цель данной работы провести анализ применяемых методов нечеткого сравнения, которые позволят получить наибольшую эффективность при обработке поступающих данных.
Для характеристики алгоритмов нечеткого сравнения используется понятие метрика или в более обобщенном варианте — расстояние.
В данном направлении наибольшее применение получили такие метрики как расстояния Хемминга, Левенштейна и Дамерау — Левенштейна. Также для проведения анализа были рассмотрены такие алгоритмы как: алгоритм нечетко поиска с индексацией и Метод N-грамм. Были рассмотрены и другие алгоритмы нечеткого сравнения, однако они оказались малоэффективны для типа данных, который использовались в эксперименте.
Расстояние Хэмминга — метрика, показывающая число позиций, в которых соответствующие символы двух слов одинаковой длины различны. В более общем случае расстояние Хэмминга применяется для строк одинаковой длины любых ограниченных алфавитов и служит метрикой различия (функцией, определяющей расстояние) объектов одинаковой размерности [1,2].
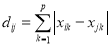
Данный алгоритм показывает большую эффективность, когда в обрабатываемых данных встречаются редкие, но большие ошибки. В рассматриваемом случае, зачастую ошибки возникают при ручном в вводе, поэтому основная проблема заключается в нахождении расхождения при небольших ошибках. Также в рамках рассматриваемой задачи, алгоритм имеет большой недостаток — в качестве вычисляемого расстояния находится «разность» между двумя символами, и при работе с расширенным алфавитом применяемый метод вносит большую погрешность при наличии нескольких языков.
Расстояние Левенштейна — метрика, измерения разности между двумя последовательностями символов. Она определяется как минимальное количество операций на каждый символ строки (вставки, удаления, замены) для превращения одной последовательности символов в другую. Каждой операции можно назначить свою цену.
Расстояние Левенштейна и его обобщения активно применяется для исправления ошибок в слове (в поисковых системах, базах данных, при вводе текста, сравнения текстовых файлов, при автоматическом распознавании отсканированного текста).
Однако метод показывает малую эффективность в ситуациях, при сравнении строк, в которых имеются перестановки слов.
Цены операций могут зависеть от вида операции (вставка, удаление, замена) и/или от участвующих в ней символов, разную вероятность разных ошибок при вводе текста, использование малоиспользуемых символов, или символов, которые маловероятно могут использоваться в середине слова и т. д.
Пусть S1 и S2 — две строки (длиной M и N соответственно) над некоторым алфавитом, тогда расстояние d(S1, S2) можно подсчитать по следующей формуле: d(S1, S2) = D(M, N), где


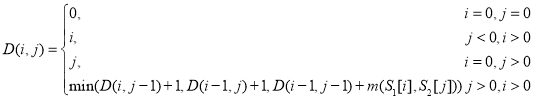
где m(a,b) равна нулю, если a = b и единице в противном случае;
min(a, b, c) возвращает наименьший из аргументов.
Здесь шаг по i символизирует удаление (D) из первой строки, по j — вставку (I) в первую строку, а шаг по обоим индексам символизирует замену символа (R) или отсутствие изменений (M).
Большим преимуществом перед ранее рассмотренным алгоритмом является возможность сравнения нескольких строк и универсальность алфавита, что позволяет получить большую эффективность при сопоставлении данных, содержащих с алфавиты сразу нескольких языков.
Расстояние Дамерау — Левенштейна (названо в честь учёных Фредерика Дамерау и Владимира Левенштейна) — это мера разницы двух строк символов, определяемая как минимальное количество операций вставки, удаления, замены и транспозиции (перестановки двух соседних символов), необходимых для перевода одной строки в другую [3]. Является модификацией расстояния Левенштейна: к операциям вставки, удаления и замены символов, определённых в расстоянии Левенштейна добавлена операция транспозиции (перестановки) символов.
Расстояние Дамерау — Левенштейна между двумя строками a и b определяется функцией da,b(|a|,|b|) как:

Применение алгоритмов с использованием нахождения расстояния Дамерау — Левенштейна имеет огромное преимущество, заключающееся в наличии операции транспозиции. В своих исследованиях Фредерик Дамерау показал, что 80 % ошибок при наборе текста человеком являются транспозициями.
Метод N-грамм представляет модель последовательностей в частности природного языка с использованием статистических свойств н грамм. Идея данного метода была описана К. Шенноном в работе «теория информации» и заключалась в том, чтобы, учитывая последовательность букв рассчитать вероятность появления последовательности каждой буквы.
N-грамм модели широко используются в статистической обработке естественного языка.
Из всех ранее рассмотренных способов для дальнейшего построения математической модели, выделяется модифицированный метод интеллектуального сравнения Дамерау-Левенштейна, поскольку он наиболее подходящий под поставленную задачу, в виду учета операции транспозиции, которая показывает хорошую эффективность при сравнениях строк, где имеет место перестановки слов и частей слов местами, а также перестановка символов при ошибочном ручном написании.
Литература :
- Hamming distance: The number of digit positions in which the corresponding digits of two binary words of the same length are different (Federal Standard 1037C)
- Харитоненков, А.В. «Поиск на неточное соответствие: коды Хемминга», http://www.jurnal.org/articles/2009/inf32.html (дата обращения 10.03.2021)
- Расстояние Дамерау — Левенштейна, URL: https://ru.wikipedia.org/wiki/Расстояние_Дамерау_-_Левенштейна (дата обращения 01.03.2021)

