Ключевые слова: машинное обучение, обучение без учителя, кластеризация, метод k-средних, DBSCAN, агломеративная кластеризация, иерархическая кластеризация.
В сегодняшнем мире машинное обучение получило широкую популярность. С помощью машин решается множество задач, машинное обучение проникает во все сферы нашей жизни: от чат-бота до диагностики раковых опухолей на ранних стадиях. Все больше задач, которые человек пытается отдать искусственному интеллекту.
Сегодня машинное обучение разделяют на 3 типа:
- Обучение с учителем;
- Обучение без учителя;
- Обучение с подкреплением.
Обучение с учителем представляет из себя процесс, аналогичный обучению человека. Есть данные, сеть и человек, который пишет нейронную сеть. В этом случае человек заранее обрабатывает данные, относя каждый объект к классу. Нейронная сеть учится на полностью готовых, размеченных человеком данных [1].
Обучение без учителя отличается тем, что данные не размечены. Рассматривая пример отнесения объекта к классу, можно сказать, что сеть ищет закономерности в наборе данных без вмешательства человека и сама определяет количество классов [1].
Обучение с подкреплением — вид машинного обучения, при котором сеть обучается, взаимодействуя со средой, в которую ее поместили. Она реагирует на сигналы именно среды, а не человека, который ее пишет. В этом состоит основная разница между обучением с учителем и обучением с подкреплением [2].
На данный момент обучение без учителя представляет наибольший интерес, т. к. данные в реальном мире крайне редко размечены и подготовлены для обучения сети. В данной статье будут рассмотрены алгоритмы обучения без учителя (кластеризация) и приведена сравнительная аналитика методов.
Кластеризация — задача разбиения множества объектов на кластеры (группы) по уровню подобия (схожести). Каждая группа должна содержать максимально похожие друг на друга объекты. При этом объекты из разных групп должны быть максимально различны. Количество кластеров заранее неизвестно, его необходимо определить в процессе работы.
Существует множество различных алгоритмов кластеризации. Каждый из них имеет свои преимущества и недостатки. Невозможно определить лучший алгоритм, т. к. зачастую один и тот же алгоритм на одном наборе данных продемонстрирует только свои преимущества, а на другом — только недостатки.
Для демонстрации работы алгоритмов сгенерировано несколько разных наборов данных (Рис.1). Чтобы провести сравнение трех алгоритмов будем тестировать каждый алгоритм на каждом наборе данных.
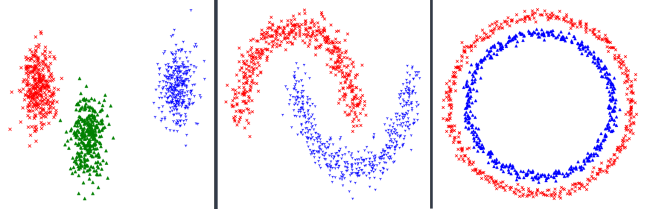
Рис. 1. Распределение наборов данных
Рассмотрим три алгоритма кластеризации:
- Метод k-средних;
- Метод DBSCAN;
- Агломеративный метод.
Метод k-средних
Отличительной чертой данного метода является наличие центроидов каждого кластера. Центроидом является точка, находящаяся посередине кластера. Каждый рассматриваемый объект будет относиться к кластеру, расстояние до которого минимально [3].
На самом первом этапе алгоритма центроиды выбираются случайно или же по некоторому заранее заданному правилу. Следующим этапом является отнесение объекта к какому-либо кластеру. После этого происходит перерасчет координат центроида. Это повторяется на каждом шаге, т. е. после каждого нового кластеризованного объекта, пока не будет исчерпано входное множество. После этого работу алгоритма можно считать законченной.
Метод DBSCAN
Данный метод основан на плотности данных в пространстве признаков. Алгоритм группирует плотнорасположенные объекты вместе, а объекты, находящиеся дальше определенного расстояния, считает шумовыми точками [4].
Работа алгоритма начинается с произвольной точки, которая не была рассмотрена ранее. Выбирается окрестность точки, определенного радиуса. Если она содержит достаточное количество точек, чтобы объединить их в один кластер, происходит объединение. Если найдена точка, принадлежащая какому-либо кластеру, то ее окружность тоже является частью кластера. Следовательно, все точки, находящиеся в ее области, тоже являются частью этого кластера. Этот процесс продолжается пока не останется свободных точек. Все точки будут либо принадлежать одному кластеру, либо являться шумовыми точками.
Агломеративный метод
Является частным случаем иерархической кластеризации. В данном методе кластеры представляются в виде иерархии. Агломеративный метод представлен как подход «снизу-вверх», т. е. каждый объект на первом этапе представляет из себя отдельный кластер [5]. На следующем шаге измеряется расстояние между кластерами, и ближайшие пары кластеров объединяются по мере продвижения вверх по иерархии. Этот процесс продолжается пока все данные не будут объединены в один кластер, либо не наступит условие остановки метода. В качестве условия может выступать определенное расстояние между кластерами.
Сравнение методов
Рассмотрим первый набор данных. Хаотично расположенные точки, но легко разделимы визуально.
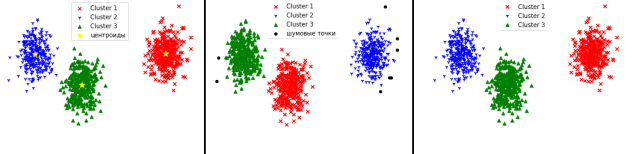
Рис. 2. Работа методов на первом наборе данных
Метод k-средних очень хорошо справляется с данными, в которых кластеры выделены явно. На этом наборе данных видно, что метод кластеризовал данные очень точно.
Метод DBSCAN не смог отнести некоторые точки к кластерам и посчитал их шумовыми.
Агломеративный метод отлично справился с задачей.
Рассмотрим второй набор данных. Он является более сложным, т. к. не является линейно разделимым.
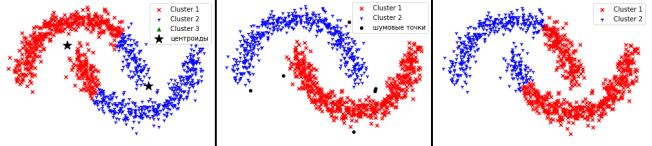
Рис. 3. Работа методов на втором наборе данных
Как мы видим на рис.3, метод k-средних не смог верно разделить данные. Это связано с тем, что идея алгоритма заключается в том, что необходимо находить точки вокруг центров.
Метод DBSCAN кластеризовал данные точно, определив несколько точек, как шумовые. В этом случае данные располагаются довольно-таки плотно. Это облегчает процесс кластеризации для метода.
Агломеративный метод отработал практически, как и метод k-средних.
Рассмотрим третий набор данных.
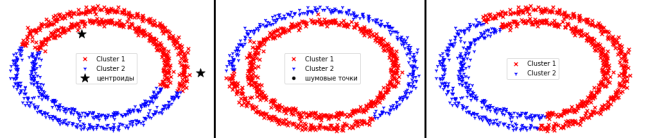
Рис. 4. Работа методов на третьем наборе данных
Третий набор данных оказался наиболее сложным для всех методов.
Метод k-средних правильно определил лишь половину объектов каждого класса.
DBSCAN полностью определил все данные относящиеся к первому кластеру, но при этом неверно определил часть данных второго кластера.
Агломеративный метод и в этом случае оказался близок к методу k-средних.
Таким образом, можно сделать вывод, что на плотносгрупированных данных все методы хорошо отработали. Если форма данных произвольная, метод DBSCAN показывает лучшие результаты, но его недостатком является то, что в любом наборе данных будут шумовые точки. Если данные собраны в группы в произвольной форме, удобен метод агломеративной кластеризации.
Сгенерированные наборы данных хорошо показали, что нельзя определить лучший метод кластеризации. Выбор метода должен быть обусловлен, в первую очередь, входными данными.
Литература:
- Уоссермен Ф. Нейрокомпьютерная техника: теория и практика. — 1992.
- Саттон Р. С., Барто Э. Г. Обучение с подкреплением //М.: Бином. — 2011.
- Arthur D., Vassilvitskii S. How slow is the k-means method? //Proceedings of the twenty-second annual symposium on Computational geometry. — 2006. — С. 144–153.
- Ester M. et al. A density-based algorithm for discovering clusters in large spatial databases with noise //Kdd. — 1996. — Т. 96. — №. 34. — С. 226–231.
- Gowda S. D. et al. An hybrid validity index for dynamic cut-off in hierarchical agglomerative clustering //2014 International Conference on Advances in Computing, Communications and Informatics (ICACCI). — IEEE, 2014. — С. 2205–2211.

