Предлагаемая вниманию читателей статья посвящена вопросу, стоящему довольно далеко от центральной линии развития математической науки.
Священные, волшебные, загадочные, таинственные совершенные… Как только их не называли. Они пользовались особой популярностью у прорицателей, астрологов и врачевателей. Привлекающие своей красотой, наполненные внутренней гармонией, доступные, но по-прежнему непостижимые, скрывающие за кажущейся простотой множество тайн… Знакомьтесь: магические квадраты – удивительные представители воображаемого мира чисел.
Учение о магических квадратах занимало в математике значительное место лишь в тот период времени, когда всем руководили суеверия и астрология; в дальнейшем при возникновении новых естественнонаучных и технических задач теория магических квадратов стала не нужна. Однако учение о магических квадратах до сих пор может представлять интерес для любителей математики, в первую очередь для учащихся, в силу простоты и наглядности задач, не говоря уже о том, что это учение представляет собой благодарное поле приложения ряда более теоретико-числовых концепций.
Предлагаю вниманию читателя рассмотреть наиболее известные методы построения магических квадратов с нечетным числом клеток. При этом мы ограничиваемся лишь «классическими» магическими квадратами, т.е. квадратами, состоящими из последовательных натуральных чисел от 1 до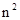 
.
Числовым квадратом порядка n, где n – некоторое положительное целое число, мы будем называть квадрат, разбитый на n2 клеток, в которых размещены ( в некотором порядке) целые числа от 1 до 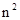. Числовой квадрат мы будем называть магическим, если суммы, получаемые от сложения чисел каждого горизонтального ряда, каждого вертикального ряда и обеих диагоналей, одинаковы. Так как квадрат порядка n и сумма 
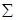чисел каждого ряда одинакова, то сумма всех чисел, размещенных в магическом квадрате, равна 
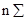. С другой стороны, она равна[3]
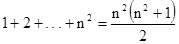
Следовательно,
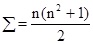. (1)
Условия равенства суммы элементов отдельных строк, столбцов и диагоналей числу 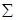мы будем называть условиями магичности этих строк, столбцов и диагоналей.[3]
Пример магического квадрата порядка 4 приведен на рис.1. (это так называемый квадрат Дюрера, изображенный на его гравюре «Меланхолия»). Для него в согласии с формулой (1),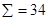 
.
|
16 |
3 |
2 |
13 |
|
5 |
10 |
11 |
18 |
|
9 |
6 |
7 |
12 |
|
4 |
15 |
14 |
1 |
Рис.1. Квадрат Дюрера
Несмотря на то, что в свое время (особенно в XVI- XVIII веках) магические квадраты были предметом пристального изучения известных математиков, все же она не может считаться завершенной. Достаточно сказать, что до сих пор не известен никакой общий метод построения всех магических квадратов данного порядка n. Можно лишь утверждать, что это число делится на 8, так как из любого магического квадрата поворотами на 90
вокруг центра и отражениями в сторонах получаются еще 7 новых магических квадратов[4].
Клетки магического квадрата порядка n мы будем обозначать парами целых чисел (x,y) – их координатами, где х – номер вертикального ряда, у – номер горизонтального ряда, на их пересечении находится данная клетка[2]. При этом вертикальные мы нумеруем слева направо, а горизонтальные – снизу вверх. В качестве номеров мы будем использовать числа
0, 1, 2, . . . , n-1 (2)
Сдвигая основной квадрат параллельно самому себе на векторы с целочисленными координатами, делящимися на n, мы получим систему налегающих друг на друга квадратов порядка n, покрывающую всю плоскость. Две клетки, принадлежащим двум таким квадратам и занимающие относительно них одинаковое положение, мы будем называть эквивалентными. В дальнейшем эквивалентные клетки будут играть одинаковую роль и будут рассматриваться как одинаковые. Каждое целое число z=1, 2, . . ., n2 мы можем записать в виде
z=nr+(s+1),
где r и s – некоторые числа системы (2), однозначно определенные числом z и, обратно определяющее это число. Мы будем числа r и z называть координатами числа z[2].
Например, при n=3 координаты чисел
z=1, 2, 3, 4, 5, 6, 7, 8, 9
имеют соответственно вид
(r,s)=(0,0), (0,1), (0,2), (1,0), (1,1), (1,2), (2,0), (2,1), (2,2).
При задании некоторого магического квадрата порядка n каждой паре r,s сопоставляется пара чисел х, у – координаты клетки квадрата, в которую вписано число с координатами r, s. Другими словами, числа х и у являются функциями чисел r и s. Обозначая эти функции буквами f и g, мы получим, следовательно, что х = f(r, s) и у = g(r, s).
В дальнейшем любую пару f(r, s) и g(r, s) мы будем называть методом построения магических квадратов[2].
Описанное сведение задачи построения магического квадрата к задаче построения пары функций f(r, s) и g(r, s) позволяет, в частности, классифицировать способы построения магических квадратов в зависимости от характера этих функций.
Индийский метод.
Индийский метод составления магических квадратов (иногда называемые также сиамским) является, по-видимому, самым древним алгоритмом построения магических квадратов произвольного нечетного порядка n=2m+1. этот алгоритм описывают следующими правилами[2]:
1. Числа от 1 до n2 поочередно вписываются в клетки основного квадрата.
2. Если некоторое правило требует вписать данное число в клетку, лежащую вне основного квадрата, то вместо этого рассматриваемое число вписывается в эквивалентную клетку основного квадрата.
3. Число 1 вписывается в среднюю клетку верхнего ряда, т.е. в клетку с координатами (m, 2m).
4. Если число z вписано в клетку с координатами (х, у), то следующее число z+1 вписывается в клетку с координатами (х+1, у+1), т.е. в клетку, смежную с клеткой (х, у), в направлении восходящей диагонали, при условии, что эта последняя клетка еще свободна от чисел.
5. Если клетка с координатами (х+1, у+1) уже занята некоторым числом, то число z+1 вписывается в клетку с координатами (х, у-1), т.е. в клетку, непосредственно примыкающую снизу к клетке (х, у). (оказывается это всегда возможно, т.е. клетка (х, у-1) обязательно свободна от чисел).
На рис.2 изображен магический квадрат третьего порядка, построенный индийским методом. Для ясности в этом рисунке заполнены также некоторые клетки вне основного квадрата. Не описывая подробно это построение, мы укажем лишь, что число 1 вписано на основании правила 1 и 3, число 2 – на основании правил 4 и 2, число 3 – на основании правил 4 и 2, число 4 – на основании правил 5 и 2, число 5 – на основании правила 4, число 6 – на основании правила 4, число 7 – на основании правил 5 и 2, число 8 – на основании правил 4 и 2 и, наконец, число 9 – на основании правил 4 и 2.
|
|
9 |
2 |
4 |
|
8 |
1 |
6 |
8 |
|
3 |
5 |
7 |
3 |
|
4 |
9 |
2 |
|
Рис.2. магический квадрат третьего порядка построенный индийским методом.
Сущность индийского метода лучше всего уясняется, если не обращать внимание на правило 2, т.е. если не заменять внешних клеток эквивалентными. При таком упрощении применение алгоритма сводится к заполнению клетки (m, 2m) числом 1 и следующий за ней вверх по диагонали клеток (m+1, 2m+1), (m+2, 2m+2), . . ., (m+k, 2m+k), . . . числами 2, 3, . . . , k+1, . . ., до тех пор, пока не встретится клетка, эквивалентная клетке (m, 2m), что, очевидно, произойдет при k = n. Под последней из заполненных клеток, (это будет клетка (m+n-1, 2m+n-1) = (3m, 4m) с числом n), т.е. в клетке (3m, 4m-1), помещается число n+1, и с этой клетки начинается новый диагональный ряд, который, как легко видеть, кончится на числе 2n, так что число 2n+1 помещается под клеткой с числом 2n. Следующий диагональный ряд кончится на числе 3n, и т.д. этот процесс остановится, когда мы дойдем до числа n2. В результате мы получим n диагональных рядов чисел по n чисел в ряду, составляющих своеобразную «лесенку» (см. рис.4 для n=3 и n=5)[2].
Причем летка построенной «лесенки», содержащая некоторое число z(z = 1, 2, . . .,n2), имеет координаты[2]
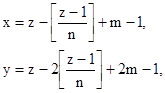(3)
где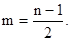 
действительно, для чисел z = 1, 2, . . ., n первого диагонального ряда эти формулы дают правильные координаты (m+z-1, 2m+z-1) соответствующих клеток.
|
|
|
9 |
|||||||
|
|
6 |
8 |
|
||||||
|
|
|
3 |
5 |
7 |
|
||||
|
|
2 |
4 |
|
||||||
|
1 |
|
||||||||
|
|
25 |
|||||||||||||||||||
|
24 |
|
|||||||||||||||||||
|
|
|
23 |
|
|||||||||||||||||
|
20 |
22 |
|
||||||||||||||||||
|
|
|
19 |
21 |
|
||||||||||||||||
|
18 |
|
|||||||||||||||||||
|
|
|
15 |
17 |
|
||||||||||||||||
|
|
14 |
16 |
|
|||||||||||||||||
|
|
|
|
13 |
|
||||||||||||||||
|
|
10 |
12 |
|
|||||||||||||||||
|
|
|
9 |
11 |
|
||||||||||||||||
|
8 |
|
|||||||||||||||||||
|
5 |
7 |
|
||||||||||||||||||
|
|
|
4 |
6 |
|
||||||||||||||||
|
3 |
|
|||||||||||||||||||
|
|
2 |
|
||||||||||||||||||
|
1 |
|
|||||||||||||||||||
Рис.3. «лесенка» для n=3 и n=5.
Индийский метод является линейным методом[2]
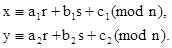
с коэффициентами
а1= -1, b1=1, c1=m,
a2= -2, b2=1, c2=2m.
Вы видите построение магического квадрата 7-го порядка рис.4.
|
|
31 |
40 |
49 |
2 |
11 |
20 |
|
|
30 |
39 |
48 |
1 |
10 |
19 |
28 |
30 |
|
38 |
47 |
7 |
9 |
18 |
27 |
29 |
38 |
|
46 |
6 |
8 |
17 |
26 |
35 |
37 |
46 |
|
5 |
14 |
16 |
25 |
34 |
36 |
45 |
5 |
|
13 |
15 |
24 |
33 |
42 |
44 |
4 |
13 |
|
21 |
23 |
32 |
41 |
43 |
3 |
12 |
21 |
|
22 |
31 |
40 |
49 |
2 |
11 |
20 |
|
Рис.4.Магический квадрат 7-го порядка.
Индийский метод, не оставляет желать ничего лучшего в отношении простоты и легкости применения, страдает тем недостатком, что для каждого нечетного n он дает лишь один, вполне определенный, магический квадрат.
Метод Москопула
В методе византийского ученого Москопула, как и в индийском методе, указывается некоторый алгоритм последовательного заполнения клеток основного квадрата числами от 1 до n2. Порядок заполнения клеток по этому способу такой же, как порядок обегания шахматной доски конем, двигающимся вверх и направо (поэтому метод Москопула иногда называют метод коня)[1].
Первые два правила в точности совпадают с соответствующими правилами 1 и 2 индийского метода. Остальные правила формулируются следующим образом[2]:
3. Если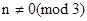 
, то начальная клетка, в которую вписывается число 1, выбирается произвольно; если же 
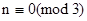, то за эту клетку принимается средняя клетка нижнего горизонтального ряда, т.е. клетка с координатами (m,0).
4. Если некоторое число z вписано в клетку с координатами (х, у), то число z+1 вписывается в клетку с координатами (х+1, у+2) при улови, что эта клетка еще свободна от чисел.
5. Если клетка с координатами (х+1, у+2) уже занята некоторым числом, то число z+1 вписывается в клетку с координатами (х, у+4), т.е. в клетку расположенную в том же вертикальном ряду, что и клетка с числом z, но находящуюся на четыре клетки выше. Рис.5 иллюстрирует построение магического квадрата пятого порядка по способу Москопула.
|
|
|
|
21 |
|
|
|
6 |
|
|
|
||
|
12 |
25 |
8 |
16 |
4 |
|
|
18 |
|
14 |
22 |
10 |
|
|
11 |
24 |
7 |
20 |
3 |
|
|
17 |
5 |
13 |
21 |
9 |
17 |
|
23 |
6 |
19 |
2 |
15 |
23 |
|
4 |
12 |
25 |
8 |
16 |
|
|
10 |
18 |
1 |
14 |
22 |
|
Рис.5. Магический квадрат пятого порядка
Для изучения метода Москопула, как и раньше, отвлечемся от правила 2, т.е. не будем заменять внешние клетки эквивалентными им клетками основного квадрата. Тогда, если мы вписали число 1 в клетку (х0, у0), то число 2 мы должны вписать в клетку (х0+1,у0+1), число 3 в клетку (х0+2,у0+4) и вообще число z – в клетку (х0+z-1,у0+2(z-1)), и так до тех пор, пока не встретим клетку, эквивалентную уже занятой. Очевидно, что это произойдет при z=n+1. Поэтому, вписав число n в клетку (х0+n-1,у0+2(n-1)), мы число n+1 должны вписать не в клетку (х0+n,у0+2n), эквивалентную исходной клетке, а– в соответствии с правилом 5 – в клетку (х0+n-1,у0+2(n+1)). Дальнейшее вписывание мы должны опять производить по «ходу коня», пока снова не наткнемся на клетку, эквивалентную уже занятой, что произойдет при z=2n+1, после чего мы должны совершить «скачок вверх» и т.д. при помощи индукции получаем, что при этом построении число z=1, 2, . . ., n2 опадает в клетку с координатами[2]
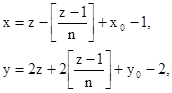
Получили, что метод Москопула является линейным методом с коэффициентами
а1= -1, b1=1, c1=х0,
a2= 2, b2=2, c2=у0.
Метод Москопула верен для любого нечетного n.
Так же рассмотрим построение магического квадрата 9-ого порядка методом Москопула рис.6.
|
|
|
|
|
|
|
|
55 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
38 |
79 |
30 |
71 |
22 |
63 |
14 |
46 |
6 |
|
|
58 |
18 |
50 |
|
42 |
74 |
34 |
66 |
26 |
|
37 |
78 |
29 |
70 |
21 |
62 |
13 |
54 |
5 |
|
|
57 |
17 |
49 |
9 |
41 |
73 |
33 |
65 |
25 |
57 |
|
77 |
28 |
69 |
20 |
61 |
12 |
53 |
4 |
45 |
77 |
|
16 |
48 |
8 |
40 |
81 |
32 |
64 |
24 |
56 |
16 |
|
36 |
68 |
19 |
60 |
11 |
52 |
3 |
44 |
76 |
36 |
|
47 |
7 |
39 |
80 |
31 |
72 |
23 |
55 |
15 |
47 |
|
67 |
27 |
59 |
10 |
51 |
2 |
43 |
75 |
35 |
67 |
|
6 |
38 |
79 |
30 |
71 |
22 |
63 |
14 |
46 |
|
|
26 |
58 |
18 |
50 |
1 |
42 |
74 |
34 |
66 |
|
Рис.6. Магического квадрата 9-го порядка методом Москопула
Метод альфила
Метод альфила вполне аналогичен методу Москопула, только вместо хода коня в этом методе используется движение по диагонали через одну клетку (по этому закону в старинных шахматах двигался предок современного слона – так называемых альфил, от которого и происходит название метода)[1].
Как и для метода Москопула, первые два правила метода альфила совпадают с провилами 1 и 2 индийского метода. Остальные правила формулируются следующим образом[2]:
3. Число 1 вписывается в клетку с координатами (0, 1).
4. Если некоторое число z вписано в клетку с координатами (х, у), то число z+1 вписывается в клетку с координатами (х+2, у+2) при улови, что эта клетка еще свободна от чисел.
5. Если клетка с координатами (х+2, у+2) уже занята некоторым числом, то число z+1 вписывается в клетку с координатами (х+1, у+3), т.е. в клетку, получающуюся из клетки с числом z «удлиненным ходом коня».
Пример построения магического квадрата пятого порядка по методу альфила приведен на рис.7.
|
|
|
|
|
6 |
|
|
|
|
|
24 |
8 |
17 |
|
15 |
|
|
21 |
10 |
19 |
3 |
12 |
|
|
23 |
7 |
16 |
5 |
14 |
23 |
7 |
|
9 |
18 |
2 |
11 |
25 |
9 |
18 |
|
20 |
4 |
13 |
22 |
6 |
20 |
4 |
|
1 |
15 |
24 |
8 |
17 |
|
|
|
12 |
21 |
10 |
19 |
3 |
|
|
Рис.7. Магический квадрат пятого порядка по методу альфила.
Аналитически метод альфила записывается формулами[2]
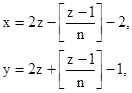
откуда следует, что метод альфила является линейным методом с коэффициентами
а1= -1, b1=2, c1=0,
a2= 1, b2=2, c2=1.
Для каждого n метод альфила дает только один магический квадрат.
Метод Баше
Рассмотрим еще один из методов построения магических квадратов нечетного порядка предложенный Баше де Мезириаком. Он известен также как метод террас[4].
Для построения магического квадрата по методу Баше следует выбрать на плоскости n соседних диагональных рядов, содержащих по n клеток и таких, что средняя клетка каждого ряда принадлежит нисходящей диагонали основного квадрата. Клетки левого верхнего ряда заполняются снизу вверх числами 1,2, …, n , клетки следующего ряда – числами n+1, n+2, …, 2n и вообще клетки p-го ряда, где 1<p<n,- числами (p-1) n+1, (p-1) n+2,……., pn[4]. Заполненные таким образом клетки частью расположены внутри основного квадрата, частью - вне его, причем внешние клетки образуют по бокам основного квадрата четыре совершенно одинаковых выступа или террасы рис.8. Следовательно, перенеся клетки террас в основной квадрат, что легко достигается параллельным перенесением этих террас, мы заполним весь основной квадрат числами от 1 до n. Оказывается, что получающийся таким образом числовой квадрат является магическим рис.9.
|
9 |
|
|||||||||||||||
|
|
8 |
|
18 |
|
||||||||||||
|
7 |
|
17 |
|
27 |
|
|||||||||||
|
|
6 |
|
16 |
|
26 |
|
36 |
|
||||||||
|
|
5 |
|
15 |
|
25 |
|
35 |
|
45 |
|
||||||
|
4 |
|
14 |
|
24 |
|
34 |
|
44 |
|
54 |
|
|||||
|
3 |
|
13 |
|
23 |
|
33 |
|
43 |
|
53 |
|
63 |
|
|||
|
|
2 |
|
12 |
|
22 |
|
32 |
|
42 |
|
52 |
|
62 |
|
72 |
|
|
1 |
|
11 |
|
21 |
|
31 |
|
41 |
|
51 |
|
61 |
|
71 |
|
82 |
|
10 |
|
20 |
|
30 |
|
40 |
|
50 |
|
60 |
|
70 |
|
80 |
|
|
|
|
19 |
|
29 |
|
39 |
|
49 |
|
59 |
|
69 |
|
79 |
|
||
|
28 |
|
38 |
|
45 |
|
55 |
|
65 |
|
75 |
|
|||||
|
|
37 |
|
47 |
|
57 |
|
67 |
|
77 |
|
||||||
|
6 |
|
56 |
|
66 |
|
76 |
|
|
||||||||
|
55 |
|
65 |
|
75 |
|
|
||||||||||
|
64 |
|
74 |
|
|
||||||||||||
|
73 |
|
|||||||||||||||
Рис8. Метод террас
|
5 |
46 |
15 |
56 |
25 |
66 |
35 |
76 |
45 |
|
54 |
14 |
55 |
24 |
65 |
34 |
75 |
44 |
4 |
|
13 |
63 |
23 |
64 |
33 |
74 |
43 |
3 |
53 |
|
62 |
22 |
72 |
32 |
73 |
42 |
2 |
52 |
12 |
|
21 |
71 |
31 |
81 |
41 |
1 |
51 |
11 |
61 |
|
70 |
30 |
80 |
40 |
9 |
50 |
10 |
60 |
20 |
|
29 |
79 |
39 |
8 |
49 |
18 |
59 |
19 |
69 |
|
78 |
38 |
7 |
48 |
17 |
58 |
27 |
68 |
28 |
|
37 |
6 |
47 |
16 |
57 |
26 |
67 |
36 |
77 |
Рис.9. Магический квадрат 9-го порядка по методу террас.
Аналитически система клеток определяется формулами[2]
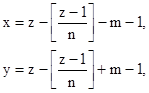
Отсюда вытекает, что метод Баше является линейным методом с коэффициентами
а1= 1, b1=1, c1= - m,
a2= -1, b2=1, c2= m.
По форме алгоритма метод Баше отличается от ранее рассмотренных алгоритмов (индийского, Москопула и альфила). Однако он приводит к тому же магическому квадрату, если правила 1, 2 и 4 совпадают с правилами индийского метода, а правила 3 и 5 формулируются следующим образом[2]:
3. Число 1 вписывается в клетку (m+1, m).
5. Если клетка с координатами (х+1, у+1) уже заполнены, то число z+1 вписывается в клетку, имеющую координаты (х+2, у), т.е. в клетку сдвинутую на две клетки вправо.
Заметим, что методом террас можно построить не только традиционный магический квадрат нечётного порядка (то есть заполненный числами от 1 до n2), но и квадрат, заполненный любыми другими числами, лишь бы разность между каждым последующим и предыдущим числом была постоянной.
Метод террас, не оставляет желать ничего лучшего в отношении простоты и легкости применения, страдает тем недостатком, что для каждого нечетного n он дает лишь один, вполне определенный, магический квадрат.
Удивительная, поистине, магическая красота, содержащаяся в магических квадратах, влечёт к себе лучшие умы человечества в течение тысячелетий. Понять её не всякому дано, но один раз осознав стройность и безжалостную строгость чисел, связанных узами магии, можно получить огромное удовольствие.
Литература
- Кордемский Б. А. Математическая смекалка. — М.: ГИФМЛ, 1958. — 576 с.
- Постников М. М. Магические квадраты. — М.: Наука, 1964. – 84c.
- Успенский Я. В. Избранные математические развлечения. — Сеятель, 1924
- Чебраков Ю. В. Теория магических матриц. — СПб.: 2008. – 179c.
