Для газовых струй, отличающихся не только скоростью, но и плотностью, только эксперимент или хорошо обоснованная математическая модель может показать, какой из параметров (отношение значения скорости, плотности или динамического напора и др.) является наиболее важным.
Турбулентное горение неперемешанных горючих газов, истекающих из прямоугольного сопла, находит широкое применение в самых различных областях техники — от обычных огнетехнических устройств ряда процессов химической технологии. В этом случае изучение их аэротермодинамических характеристик, с учетом кинетики процесса, представляет большой интерес. В тоже время детальное исследование горения неперемешанных газов, истекающих, из произвольного прямоугольного сопла непеременшанных горючих газов практически отсутствует.
Одной из целей, данной работы является выбор вида полуэмпирической формулы для определения коэффициента — турбулентной вязкости.
Для трехмерных сдвиговых свободных турбулентных струйных течений, формула Прандтля
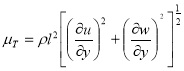 (1)
(1)
дает качественно правильные результаты, для пристенных течений.
Кроме того, формула (1) не учитывает деформацию продольной скорости по другим пространственным координатам и температуру, которые существенно влияют на результаты исследования. Также неизвестно как определить длину пути перемешивания для трехмерных струйных течений в модели (1).
В данной работе приводится некоторые результаты численного исследования горения смеси пропан — бутана, истекающего из сопла прямоугольной формы и распространяющейся в покоящейся среде воздуха. Для описания течения использованы трехмерные параболизованные системы уравнений Навье-Стокса для многокомпонентных химически реагирующих газовых смесей. Численные исследования проведены на основе эффективного метода подобных SIMPLE прямым методом решается уравнение Пуассона для определения поправки к скоростям [1].
Для вычисления турбулентной вязкости предложена для численного исследования использована модель, учитывающую молекулярный перенос, трехмерность и температурную неоднородность в виде
![]() æ
æ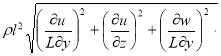
![]() , (2)
, (2)
где æ-число Кармана, α-степень влияния температуры неоднородности потока (0,5< α <0,7). Т![]() -температура горючей струи на оси симметрии, L-отношения сторон прямоугольного сопла, l-длина пути перемешивания определяется как
-температура горючей струи на оси симметрии, L-отношения сторон прямоугольного сопла, l-длина пути перемешивания определяется как
![]()
Для основного расчетного варианта исходные значения параметров брались следующим образом [2]
I. Зона окислителя: II. Зона горючего:
T1=300K u1=0; ![]() T2=1200K u2=61м/с;
T2=1200K u2=61м/с;
(С1)1=0,232; (С2)1=0; (С1)2=0; (С2)2=0,12;
(С3)1=0; (С4)1=0; (С3)2=0; (С4)2=0,88;
Pr=Sc=0.65; P1=P2=const; L=1
С точки зрения математического расчета рассмотрим четырёхкомпонентную смесь газов в зоне смешения, состоящую из кислорода O2 -индекс «1», смеси пропана — бутана (C3H8+C4H10) -«2», продуктов горения CO2+9H2O — «3», инертного газа N2 — «4». С физической точки зрение в зоне тепло — и массаобмена участвуют 6 компонентов.
В данной работе приводятся некоторые численные результаты касающиеся влияния исходных данных скорости, температуры струи и окислителя на параметры диффузионного факела.
В частности, можно отметить, что подогрев горючего и окислителя приводит к незначительному удлинению длину факела.
В этом случае соблюдаются известные закономерности изменения границы, т.е при подаче более нагретого горючего граница зоны смешения растет более медленно, однако переход к круглой форме факела затягивается, т. е. как даже при безразмерной длине по продольной координате ![]() =15 еще полностью не переходит в круглую форму.
=15 еще полностью не переходит в круглую форму.
Литература:
- С.Ходжиев. Исследования трехмерных турбулентных струи реагирующего газов, истекающеюся в спутном (затопленном) потоке в воздухе при диффузионном горении// Узб. Журнал. Проблемы механики. Тошкент. Фан, № 2, 1993. С. 28–33.
- Вулис Л. А, Ярин Л. П. Аэродинамика факела. — Л. Энергия. 1978, 216 с.

