В данной работе изложен приближенный метод расчёта свободных турбулентных осесимметричных струй, в основу которого положены физическая картина струйного течения, предложенная Г.Н.Абрамовичем и система уравнений, используемая Л.А.Вулисом.
Эффективное управление турбулентными газовыми струями при решении разнообразных технических задач [1] невозможно без анализа взаимосвязей между основными характеристиками струй. Данное обстоятельство вызывает необходимость построения физико-математических моделей, адекватно отражающих процессы тепло- и массообмена в струйных течениях и легко реализуемых в инженерных приложениях.
В связи с отсутствием единой теории турбулентных течений применяются различные модели турбулентности, приспособленные для решения конкретных задач.
Подробный обзор таких моделей и экспериментальная информация по проблемам свободной турбулентности представлена в [2].
Расчёты струйных течений после выбора модели турбулентности проводятся либо численными методами с применением ЭВМ, либо приближенными аналитическими методами. Данная работа относится ко второму направлению.
Согласно [3] процессы тепло- и массопереноса в осесимметричных струйных течениях газовых смесей могут быть описаны уравнениями вида:
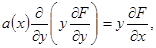(1)
где обобщенная газодинамическая функция F принимает значения
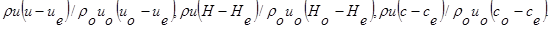
Индексы «о» и «е» соответствуют скорости, теплосодержанию смеси и концентрациям отдельных компонентов на срезе сопла и внешней границе струи соответственно;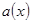 
- зависимость, полученная экспериментально [3] и содержащая отношение плотностей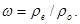 
Уравнение (1) необходимо решать при соответствующих граничных условиях, удовлетворяя решение интегральным условиям сохранения избыточных количества движения, теплосодержания и концентраций.
Физическая модель газовой струи по [4] предполагает наличие начального, переходного и основного участков, как показано на рисунке 1.
 |
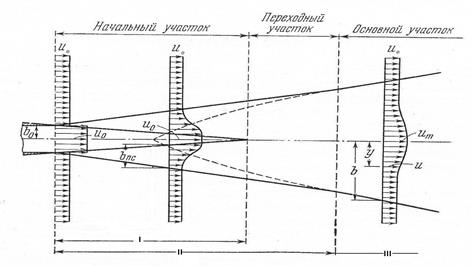Рис.1 – Схема турбулентной струи, истекающей из сопла с дозвуковой скоростью в спутный поток
В пределах каждого участка уравнение (1) решалось итерационно-интерполяционным методом [5].
Первое приближение функции Fна начальном участке было принято в виде:
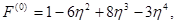(2)
где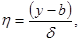 
b – полуширина потенциальной области течения (F=1), 
- толщина пограничного слоя, соответствующего виду функции F.
В результате подстановки (2) в правую часть (1) и интегрирования получено уточнённое приближение, которое в конце начального участка выглядит следующим образом:
FH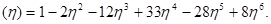
(3)
Было установлено, что полуширина струи в конце начального участка не зависит от условий истечения струи и равна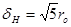 
, где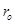 
- радиус выходного сечения сопла.
Начальное приближение функции Fна основном участке выбиралось в виде
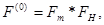(4)
где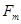 
- значение Fпри y=0, т.е. на оси струи. Последующее приближение получено в виде:
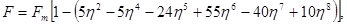(5)
где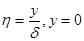 
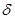, - полуширина струи.
Установлена следующая связь между 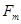и :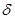
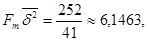
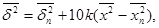
где k=const, а индекс «п» соответствует концу переходного участка.
Определены также значения 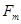и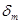 
в начальном сечении основного участка.
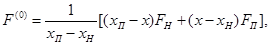Ввиду незначительной протяженности переходного участка за нулевое приближение для обобщенной функции принята следующая интерполяционная зависимость:
(6)
 |
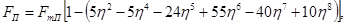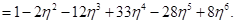где
FH
Уточнённое выражение для обобщенной функции не приведено ввиду его громоздкости.
Результаты численного анализа представлены на следующих графиках.
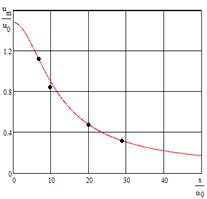
На рисунке 2 сравниваются расчетные и экспериментальные [4] значения осевой скорости при различной степени подогрева струи 
Рис. 2 - Сравнение расчётных и экспериментальных [4] значений осевой скорости при различной степени подогрева струи θ=1, 1.85, 3.25
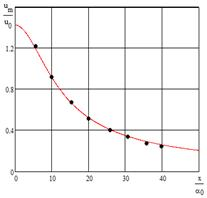
Изменение динамического давления в конечном сечении основного участка струи в сравнении с экспериментальными данными [3] представлено на рисунке 3.
 |
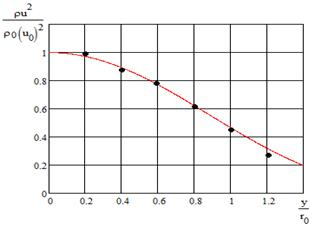Рис.3 – Изменение динамического давления в сечении 
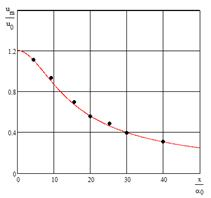
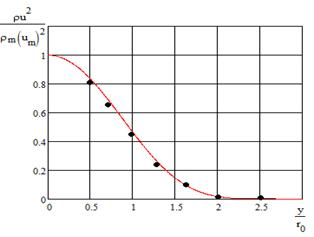Сравнение расчетных значений динамического напора в поперечном сечении основного участка с результатами точного решения [3] приведено на рисунке 4. Отклонение приближенного решения от точного незначительно.
Рис. 4 – Изменение динамического давления в сечении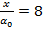 
На рисунке 5 изображены профили скорости и избыточной температуры в поперечном сечении начального участка. Если расчёт скорости не вызывает затруднений, то при расчёте температуры возникает особенность при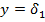 
, где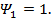 
Это ведёт к искажению профиля при 
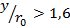. Поэтому на отрезке 
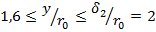использована линейная зависимость 
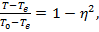рекомендованная в [4].
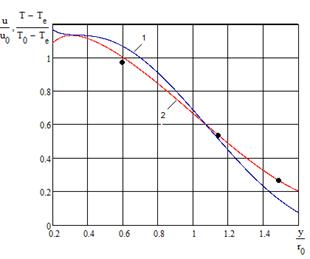
Рис. 5 – Изменение скорости (1) и температуры (2) в поперечном сечении начального участка: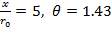 
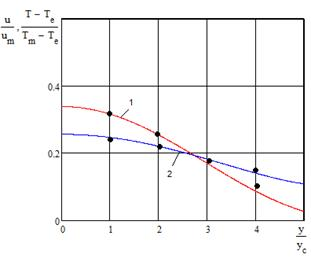
На рисунке 6 представлены профили скорости и избыточной температуры в поперечном сечении основного участка струи. Наличие особенности при 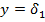не позволило использовать расчётные формулы для избыточной температуры при 
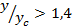, где 
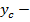значение 
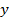, при котором 
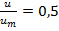. Расчёт вблизи границы смещения струи с внешней средой был приведён по формуле Тейлора [4]
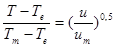. (7)
Рис. 6 – Изменение скорости (1) и избыточной температуры (2) в поперечном сечении основного участка струи: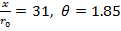 
На рисунке 7 изображено изменение температуры вдоль оси струи. При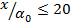 
наблюдается удовлетворительное согласование с экспериментальными данными, а при 
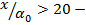с теоретическими значениями температуры, полученными в [4].
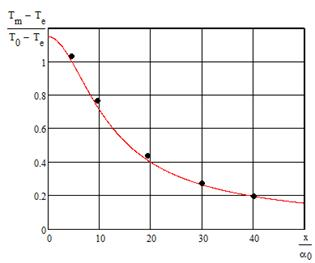
Рис. 7 – Изменение температуры на оси струи: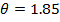 
Результаты численного анализа полученных зависимостей хорошо согласуются с экспериментальными данными, приведенными в [4]. Кроме того, установлено соответствие результатов расчёта температуры в поперечных сечениях основного участка теоретической формуле Тейлора [4].
Литература
1. Дыбан Е.Л., Мазур А.И. Конвективный теплообмен при струйном обтекании тел. – Киев: Наукова Думка, 1982. – 303 с.
2. Шец Дж. Турбулентные течения. Процессы вдува и перемешивания. – М.: Мир, 1984. – 247 с.
3. Вулис Л.А., Кашкаров В.П. Теория струй вязкой жидкости. – М.: Наука, 1965 – 431 с.
4. Абрамович Г.Н. Теория турбулентных струй. – М.: Физматгиз, 1960 – 715 с.
5. Гришин А.М., Берцун В.Н. Итерационно-интерполяционный метод и теория сплайнов. – Докл. АН СССР, 1974, т. 214,4.
