Цель работы — создание прикладной программы для расчёта процессов, происходящих при распаде топливной струи на капли в камере сгорания постоянного объёма, с возможностью визуализации процесса и отслеживания параметров струи.
Для достижения цели необходимо выбрать и реализовать в программе модели, описывающие поведение газа и капель жидкости (топлива): поведение неоднородной газовой среды, процесс распыла топлива через форсунку, движение капель в газовой среде, их распад в процессе движения, а так же столкновение друг с другом и со стенками камеры, и наконец испарение и горение.
Модель для описания состояния газовой среды.
Поскольку распыл топлива происходит в газовой среде, в первую очередь необходимо описать состояние этой среды. Параметры газа оказывают влияние как на процесс истечения топлива из сопла форсунки, так и на дальнейшее поведение капель топлива, включая их движение в пространстве, распад, столкновение, испарение и сгорание. Таким образом состояние газа во многом влияет на формирование топливного факела.
Для расчета параметров состояния и локальных скоростей газа в камере сгорания используется метод Годунова, так же называемый методом распада произвольного разрыва [1]. Данный метод позволяет определить параметры по всему объёму камеры на следующем шаге по времени t+Δt при известных параметрах на данный момент t.
Метод заключается в представлении расчётной зоны как отдельных объёмов — ячеек, каждая из которых заполнена газом с разными параметрами и которые разделены по границам перегородками — мембранами (рисунок 1). В каждый из расчётных моментов происходит мгновенное разрушение всех мембран, на границах между ячейками происходят распады произвольных разрывов (РПР). На каждой границе образуются две элементарные волны, фронты которых распространяются вдоль характеристик, идущих от границы в положительном и отрицательном направлении оси, перпендикулярной данной границе.
Вдоль положительной характеристики выполняется соотношение
вдоль отрицательной
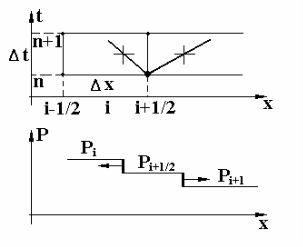
Рис. 1. Распространение фронтов волн сжатия и разряжения в одномерном случае при РПР
Тогда в одномерном случае на границе между i и (i+1) ячейками — на мембране (i+1/2):
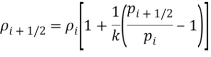при vi+1/2>0;
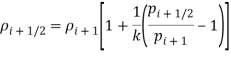при vi+1/2<0;
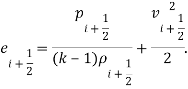
Для мембран, находящихся на границе описываемой зоны, т. е. мембран, принадлежащих только одной ячейке, формулы упрощаются, а скорость v принимается равной нулю.
Определив значения параметров всех мембран для данного момента времени t, рассчитывают значения параметров в ячейках для следующего момента времени t+Δt исходя из соотношений:
где
– поток массы через мембрану;
– количество прибывшего движения;
– импульс силы давления на границе;
– количество прибывшей энергии;
– работа, совершённая силой давления на границе.
После определения объёмных параметров M, K, E становится возможным определить и основные газодинамические параметры в ячейке.
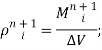
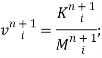
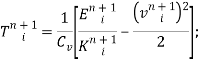
Таким образом параметры газа во всех ячейках на момент времени t+Δt определены, расчёт повторяется для следующего шага по времени.
В данном случае, рассматривается трёхмерная модель, поэтому каждая ячейка соседствует с шестью мембранами, а векторные параметры, такие как скорость v и количество движения K определяются в проекциях на оси.
Особенности реализации метода Годунова в программе.
Для всех расчётов, включающих определение состояния газа на следующем шаге по времени и поведения топливной струи, необходимо знать параметры газа в ячейках только на данный момент времени t. Так же для визуализации процесса распыла данные сохраняются во внешние файлы, таким образом необходимость в хранении в оперативной памяти всей «истории» состоянии газа полностью отпадает.
В связи с этим решено для хранения информации о состоянии газа и в ячейках и на границах использовать трёхмерный массив, содержащий параметры только на рассматриваемый момент времени, вместо четырёхмерного. Учитывая, что количество рассчитываемых временных шагов может исчисляться тысячами, это многократно снижает потребление ресурсов программой.
Вычислительная сложность [5] одного шага предложенного алгоритма Θ(n), где n — число ячеек, на которое разбита камера. Всего алгоритма Θ(n∙T), где T — число рассчитываемых шагов по времени.
Возможно снижение вычислительной сложности путём исключения повторения расчётов параметров на границах и в ячейках, которые не претерпели изменений за шаг Δt или имеют параметры равные уже рассчитанным на данном этапе. Однако, данная операция является одной из наиболее эффективных при правильной работе программы и её оптимизация по вычислительной сложности излишня.
Модель распыла через прямое сопло.
При расчете распыла топлива через прямое сопло необходимо определить скорость истечения струи из сопла, диаметр образовавшихся капель и угол раскрытия первичной струи.
Входными данными являются: диаметр d и длина сопла L, радиус скругления на входе в сопло r, подыгольное давление в форсунке p1, динамическая вязкость μl, плотность ρl и давление насыщенных паров топлива pvl (Рисунок 2).
В первую очередь определяется режим истечения из сопла, для этого рассчитывается кавитационный параметр для текущего режима [2, 4]
где pg – давление газа внешней среды. Затем рассчитывается кавитационный параметр начала кавитации
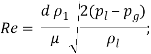
И критический кавитационный параметр (срыва потока)
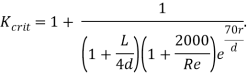
При K>Kinc и K>Kcrit истечение однофазное, при K
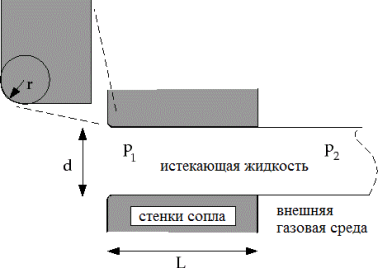
Рис. 2. Геометрические параметры сопла и однофазный режим истечения
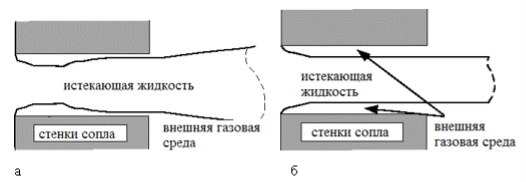
Рис. 3. Кавитационный (а) и отрывной (б) режимы истечения
Коэффициент массового расхода в зависимости от режима рассчитывается по формулам:
− для однофазного
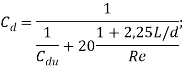
− для кавитационного
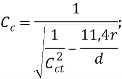
− для отрывного
Идеальный и действительный расход через сопло
Скорость истечения жидкости из сопла зависит от режима течения и рассчитывается по формулам:
− для однофазного режима истечения
где A – площадь поперечного сечения сопла;
− для кавитационного
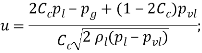
− для отрывного
Полуугол распыла из сопла:
− для однофазного и кавитационного режимов
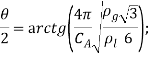
− для отрывного принимается
Диаметр капель для однофазного режима
где
– средний поверхностный диаметр капли, 
– характерный размер, 
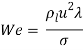– число Вебера.
Для кавитационного режима расчёт проводится по формулам
Где d23 и We определяются аналогично, а характерный размер 
при эффективном диаметре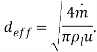 
Наконец для отрывного режима
Особенности реализации модели в программе.
Поскольку шаг по времени задаётся с тем, чтобы была устойчива модель Годунова, за один шаг из сопла происходит истечение числа капель, которые могут быть рассчитаны по формуле:
Очевидно разность положений всех Ndr капель в пространстве-времени будет много меньше погрешности возникшей из-за дискретизации расчёта, более того отдельный расчёт каждой капли на последующих этапах (распад, столкновения, испарение, горение) многократно увеличит затраты ресурсов.
По этой причине капли, распыленные соплом за один шаг по времени, объединены в несколько условных «пакетов». Во всех дальнейших расчётах полагается, что капли в одном пакете одинаковы по всем показателям. Поскольку подразумевается, что конус скоростей капель на выходе из сопла симметричен относительно оси сопла, созданные пакеты распределяются по этому конусу с равным угловым шагом.
Вычислительная сложность одного шага предложенного алгоритма Θ(n), где для n — количество сопел в рассчитываемой системе. Возможно уменьшить вычислительную сложность, если избегать повторения расчётов параметров капель на следующем шаге с такими же значениями подыгольного и внешнего давления. Однако, как сказано выше, данная операция не является определяющей для суммарного времени выполнения программы.
Большое влияние на эффективность работы программы оказывают особенности структуры данных, содержащей пакеты капель, так как практически всем подпрограммам требуется обрабатывать и изменять хранимую в них информацию, а так же создавать и удалять новые пакеты на каждом шаге расчёта.
Выбор структуры произведён из соображений, представленных в таблице 1, как видно, было принято решение в пользу двусвязного списка. Таким образом существенно уменьшены затраты вычислительных ресурсов, связанные с изменением количества пакетов.
Таблица 1
Выбор структуры данных
|
|
Доступ кэлементу |
Добавление/удаление элемента |
|
Динамический массив |
Θ(1) |
Θ(1)…Θ(n) в зависимости от реализации |
|
Двусвязный список |
Θ(n) в общем случае Θ(1) при последовательном обращении |
Θ(1) |
|
Особенности алгоритмов программы |
Доступ к элементам структуры всегда будет совершаться последовательно |
Добавление и удаление элементов происходит на каждом шаге расчёта |
Модель распада капель.
В программе используется модель аналогии Тейлора (Taylor analogy break-up model) [2, 3, 4], которая основана на рассмотрении отдельной капли, деформирующейся под действием сил поверхностного натяжения, трения о газ и вязкого трения, как осциллирующей системы из масс и пружины.
Считает, что капля распадается при деформации x, такой что x>Cb·r, где Cb=0,5 или в безразмерных величинах:
Второй закон Ньютона записанный через y и выраженный относительно этой величины принимает вид
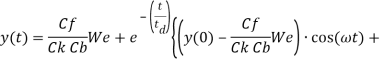
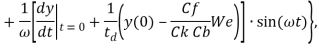
где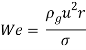 
– число Вебера; 
и 
– значение функции y и её производной на начальный момент времени, в расчётах принимались равными нулю;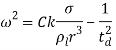 
– квадрат угловой скорости колебаний капли при 
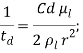u – скорость капли относительно среды; r – радиус недеформированной капли; σ – коэффициент поверхностного натяжения.
Эмпирические коэффициенты в расчетах принимались Cf = 1/3, Cd = 5, Ck = 8. Размер дочерних капель рассчитывается из закона сохранения энергии и равен
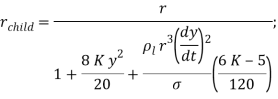
где К – экспериментальный коэффициент (
).
После распада дочерние капли в дополнение к осевой составляющей скорости (сонаправленной со скоростью родительской капли на момент распада) приобретают некоторую нормальную к осевой составляющую
Особенности реализация модели распада струи на капли в программе.
Как было сказано выше, капли объединяются в пакеты, таким образом расчёт распада производится единовременно для целого набора капель. Поскольку при одном распаде может образоваться большое количество дочерних капель, экспоненциально увеличивая количество пакетов по времени, вводится искусственное ограничение, дополнительно группирующее образовавшиеся капли в новые пакеты.
Поскольку модель распада струи позволяет определить лишь величину вектора скорости перпендикулярной скорости родительского пакета, но не её направление в трёхмерном пространстве, дочерние пакеты с равным шагом распределяются по направлениям, формируя конус скоростей. Данное решение позволяет уменьшить необходимое количество расчётов, тем не менее достаточно точно моделируя топливный факел.
Используемая модель недостаточно точно описывает поведение капель в зоне близкой к соплам форсунки, в данный момент ведётся анализ других моделей с целью их совместного применения.
Ввод и вывод данных.
Ввод данных в программу осуществляется через заранее созданный текстовый файл «input.txt», в котором описываются габариты камеры сгорания, параметры газа в ней на начальный момент времени, расположение форсунок, геометрия и направления их сопел, подыгольное давление топлива, а так же параметры для разбиения камеры на ячейки и определения шага по времени.
Вывод осуществляется в набор файлов «gas.vtk» и «spray.vtk» по одному файлу для каждого шага по времени, данный формат — внутренний для программы визуализации ParaView [6]. В файлах хранится состояние газа в камере по ячейкам: давления, температуры, плотности, вектора скоростей; а так же набор точек, каждая из которых соответствует одному пакету капель, для каждого пакета возможно просмотреть: диаметры капель, количество капель в пакете, суммарную массу топлива в одном пакете.
Общая организация программы.
Расчёт каждого отдельного шага по времени проводится в изложенном порядке в общем цикле: определения состояния газа; расчёт параметров новых капель, получившихся в результате распыла через сопла форсунок; расчёт распада существующих капель; перемещение капель в пространстве; вывод текущего шага в файлы для визуализации.
Каждый отдельный этап выполняется в своей подпрограмме, которой передаётся структура, содержащая все ячейки и границы, а так же двусвязный список пакетов капель. Такое построение позволяет разрабатывать программу блоками, иметь несколько моделей для одного процесса и по необходимости переключать их.
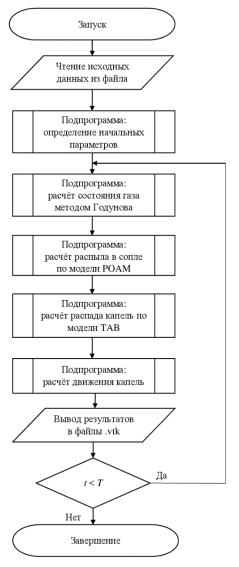
Рис. 4. Общая блок-схема программы
Полученные результаты.
В качестве теста в программу были введены параметры схожие с теми, которые возникают в двигателе 16ЧН26/26 (5Д49) на момент распыла топлива, включая температуру, давление, скорость вихря в цилиндре, а так же геометрию форсунки и её сопел.
Рис. 5. Визуализация результатов расчёта
На данном этапе программа позволяет оценить влияние параметров распыла на общую геометрию факелов: угол их раскрытия, степень закрутки вихрем. Это обеспечивает возможность простого и наглядного контроля столкновения топливных струй, которое вызывает ухудшение параметров сгорания.
Стоит отметить, что из-за моделирования камеры сгорания прямоугольным параллелепипедом и наличия в объёме газового вихря, в углах камеры возникли области повышенных давлений.
Заключение.
Разработанная программа в общем виде позволяет проследить начальный этап образования топливного факела — распыл струи и распад капель. Для полного моделирования необходимо так же учесть столкновение капель друг с другом и со стенками камеры, трение между каплями и газом. Для образования топливного факела — процессы испарения и горения, образования отработавших газов и их взаимодействия с свежим зарядом в камере.
С точки зрения реализации наибольшие технические сложности представляет расчёт столкновения капель друг с другом, так как прямой попарный расчёт предполагает вычислительную сложность Θ(n2). С учётом экспоненциального роста количества пакетов, на поздних этапах распыла данная часть расчёта будет целиком определять эффективность всей программы.
Литература:
- Годунов С. К. Численное решение многомерных задач газовой динамики. / М.: Наука, 1976.
- FLUENT 6.3 [Документация]. / FLENT Inc, 2006.
- Kaushal Nishad. Modeling and unsteady simulation of turbulent multi-phase flow including fuel injection in IC-engines. / Darmstadt, 2013.
- Nasser Ashgriz. Handbook of Atomization and Sprays. Theory and Applications. / New York: Springer Science, 2011.
- Алгоритмы: построение и анализ. / Т. Кормен, Ч. Лейзерсон, Р. Ривест, К. Штайн. — М.: Вильямс, 2013.
- Paraview. Documentation. [http://www.paraview.org/documentation/]. / Kitware Inc, 2016.
