В настоящей статье представлены выражения, позволяющие определить ковариационную функцию дважды стохастического изображения. Проведен сравнительный анализ полученной ковариационной функции с функцией для известных авторегрессионных моделей. Полученные выражения могут быть использованы для генерации изображений с заданными корреляционными свойствами.
Ключевые слова: статистический анализ изображений, авторегрессионные модели, случайные поля, дважды стохастические модели, цифровая обработка изображений, ковариационная функция
Цифровая обработка изображений сегодня приобретает все большую значимость. Действительно, такая обработка нужна в самых различных областях науки и техники. При этом важную роль при проектировании различных систем автоматической обработки играет математическое моделирование, основанное на имитации изображений [1, 7], а также включающее в себя этапы разработки алгоритмов под конкретные модели изображений. Основными задачами автоматической обработки сегодня являются: обнаружение объектов на изображении [2, 8], прогнозирование сигналов [6], а также фильтрация изображений [9, 10]. При этом спектр задач достаточно широкий и может включать в себя обработку в рамках службы заказа такси [5] или, например, имитацию изображений при проектировании систем солнечного отопления [11].
В последнее время особую популярность набирают дважды стохастические модели случайных полей, обзор которых можно найти в работах [3, 4]. Несмотря на достаточно большое число алгоритмов, предложенных для обработки таких изображений, незначительно исследованы задачи имитации изображений с заданными корреляционными свойствами.
Для решения этой задачи необходимо исследовать свойства корреляционной функции дважды стохастического случайного поля [3, 4].
Запишем следующее случайное поле:
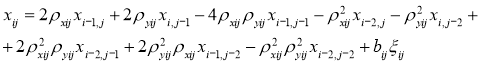 (1)
(1)
где ![]() — моделируемое случайное поле с нормальным распределением
— моделируемое случайное поле с нормальным распределением ![]() ,
, ![]() ;
; ![]() — случайное поле независимых стандартных гауссовских случайных величин
— случайное поле независимых стандартных гауссовских случайных величин ![]() ,
, ![]() ;
; ![]() и
и ![]() — коэффициенты корреляции модели с кратными корнями характеристических уравнений кратности (2,2);
— коэффициенты корреляции модели с кратными корнями характеристических уравнений кратности (2,2); ![]() — коэффициент, отвечающий за дисперсию моделируемого случайного поля.
— коэффициент, отвечающий за дисперсию моделируемого случайного поля.
Коэффициенты корреляции модели (1) представляют собой преобразованную реализацию авторегрессионной модели первого порядка.
Так как основное изображение генерируется с помощью модели с кратными корнями, то можем записать его ковариационную функцию:
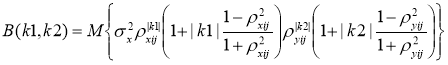 (2)
(2)
И с учетом независимости ![]() и
и ![]() :
:
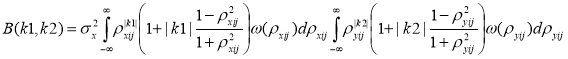 (3)
(3)
где ![]() и
и ![]() ,
, ![]() — коэффициенты корреляции модели с кратными корнями характеристических уравнений кратности (2,2).
— коэффициенты корреляции модели с кратными корнями характеристических уравнений кратности (2,2).
Наконец, после несложных преобразований искомая функция (2) при решении интеграла (3) запишется:
– если ![]() принимает четные значения, и
принимает четные значения, и ![]() принимает четные значения, то:
принимает четные значения, то:
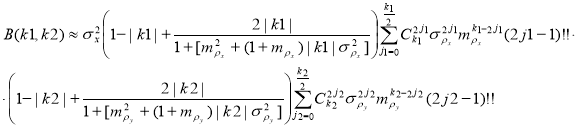 (4)
(4)
– если ![]() принимает четные значения, и
принимает четные значения, и ![]() принимает нечетные значения, то:
принимает нечетные значения, то:
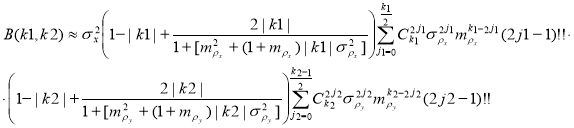 (5)
(5)
– если ![]() принимает нечетные значения, и
принимает нечетные значения, и ![]() принимает четные значения, то:
принимает четные значения, то:
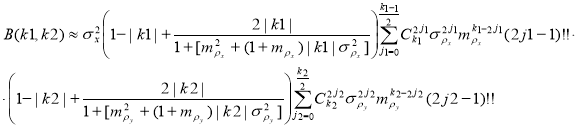 (6)
(6)
– если ![]() принимает нечетные значения, и
принимает нечетные значения, и ![]() принимает нечетные значения, то:
принимает нечетные значения, то:
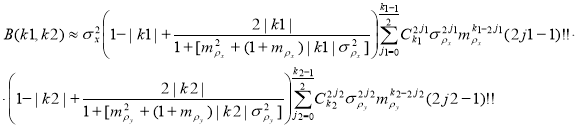 (7)
(7)
где 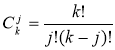 ;
; ![]() означает двойной факториал числа
означает двойной факториал числа ![]() и определяется как произведение всех натуральных нечетных чисел в отрезке [1,
и определяется как произведение всех натуральных нечетных чисел в отрезке [1, ![]() ].
].
Для определения области применения дважды стохастических полей яркости проведены исследования свойств их КФ. На рис. 1 представлены график решения интеграла (3), график КФ, найденной по выражениям (4) и график ковариационной функции стандартной авторегрессионной модели с кратными корнями характеристических уравнений кратности (2,2) или восьмиточечной модели с постоянными коэффициентами корреляции ![]() и
и ![]() . Результаты рассмотрены для сечения
. Результаты рассмотрены для сечения ![]() . Параметры модели
. Параметры модели ![]() .
.
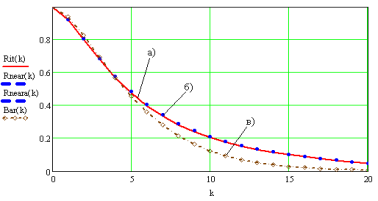
Рис. 1. Сравнительная характеристика ковариационных функций
Таким образом, представлены выражения для поиска ковариационной функции сложного дважды стохастического изображения. Стоит отметить, что данная функция представляет лишь конкретный частный случай. Однако позволяет получить более коррелированное изображение, чем при использовании аналогичной авторегрессионной модели. Кроме того, знание ковариационных связей позволяет выбирать параметры моделей таким образом, чтобы они обеспечивали заданную корреляцию на изображении.
Литература:
- Андриянов Н. А. Программа имитации обычных и смешанных случайных полей // Современные тенденции в науке, технике, образовании. Сборник научных трудов по материалам Международной научно-практической конференции: в 3-х частях. 2016. Ч. 1, С. 38–40.
- Васильев К. К., Дементьев В. Е., Андриянов Н. А. Исследование точности обнаружения и распознавания сигналов простейших геометрических форм на фоне дважды стохастической модели // Вопросы радиоэлектроники. Серия: Техника телевидения. 2015. № 6 (23). С. 67–71.
- Васильев К. К., Дементьев В. Е., Андриянов Н. А. Цифровая обработка дважды стохастических моделей случайных полей // Молодой ученый. — 2016. — № 10. — С. 137–138.
- Андриянов Н. А. Краткий обзор методов обработки дважды стохастических моделей // Наука XXI века: открытия, инновации, технологии. Сборник научных трудов по материалам Международной научно-практической конференции. В 3-х частях. Часть 3. 2016. — С. 18–20.
- Андриянов Н. А., Данилов А. Н. Сервис службы заказа такси с прогнозированием статистики на основе комплексных математических моделей // Успехи современной науки. 2016. Т. 2. № 10. — С. 114–116.
- Андриянов Н. А. Величина ошибки прогноза в точку на фоне смешанной модели сигнала // Современное научное знание: теория, методология, практика Сборник научных трудов по материалам Международной научно-практической конференции в 3-х частях. ООО «НОВАЛЕНСО». Смоленск, 2016. Ч. 3, С. 34–36.
- Дементьев В. Е., Андриянов Н. А. Использование дважды стохастических моделей случайных процессов и полей для описания сложных неоднородных сигналов // Актуальные проблемы физической и функциональной электроники. Материалы 19-й Всероссийской молодежной научной школы-семинара. 2016: УлГТУ, — С. 98–99.
- Андриянов Н. А., Кутузов В. И. Применение алгоритма обнаружения одномерных протяженных аномалий к смешанным моделям случайных полей // Современные проблемы проектирования, производства и эксплуатации радиотехнических систем. 2016. № 1 (10). С. 123–127.
- Васильев К. К., Дементьев В. Е., Андриянов Н. А. Фильтр Винера для дважды стохастических случайных процессов // Современные проблемы проектирования, производства и эксплуатации радиотехнических систем. 2016. № 1 (10). С. 119–122.
- Васильев К. К., Гаврилина Ю. Н., Андриянов Н. А. Эффективность фильтрации авторегрессионной модели с кратными корнями характеристических уравнений // Современные проблемы проектирования, производства и эксплуатации радиотехнических систем. 2016. № 1 (10). С. 130–133.
- Чичкин А. И., Андриянов Н. А. Имитация солнечного потока с помощью методов моделирования изображений // Новые направления и концепции в современной науке. Сборник научных трудов по материалам Международной научно-практической конференции 31 октября 2016 г. — С. 38–39.

