Математическая модель асинхронного двигателя с переменными ψs – ψm на выходе интегрирующих звеньев в Simulink



Данная работа является продолжением статьи [1]. Проекции векторов и выведены на основе интегрирующих звеньев с моделированием в Simulink.

В работе [1] было получено уравнение (13) для расчета ψ_sx в Script-Simulink:

Выразим потокосцепление ψ_sx по оси (+1):

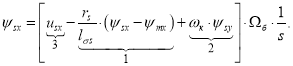
Структурная схема для определения ψ_sx представлена на рис. 1.

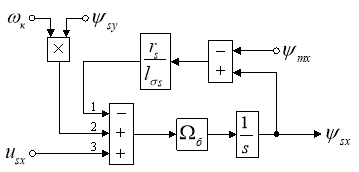
Рис. 1. Структурная схема для определения потокосцепления ψ_sx в Script-Simulink

Преобразуем структурную схему на рис. 1 в оболочку, позволяющую производить расчет коэффициентов в отдельном блоке Subsystem. Для этого вместо операторов с коэффициентами, рассчитываемыми в Script, установим блоки перемножения, к которым подведены сигналы с результатами расчетов в Simulink, как показано на рис. 2.

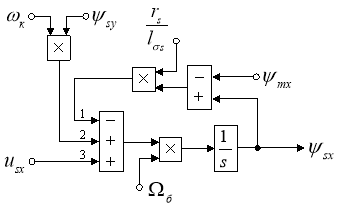
Рис. 2. Структурная схема для определения потокосцепления ψ_sx в Simulink

Для определения ψ_mx приведем уравнение (14) из работы [1]:

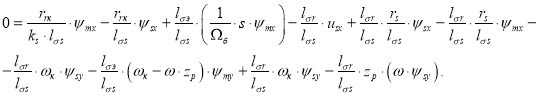
Перенесем слагаемое в левую часть:

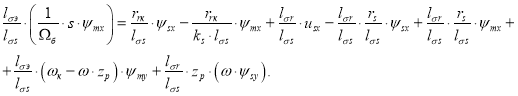
Умножим обе части уравнения на :

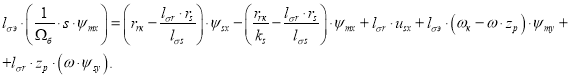
Обозначим и .

Выразим ψ_mx по оси (+1):

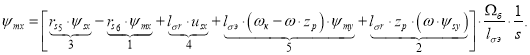
Структурная схема для определения ψ_mx приведена на рис. 3.

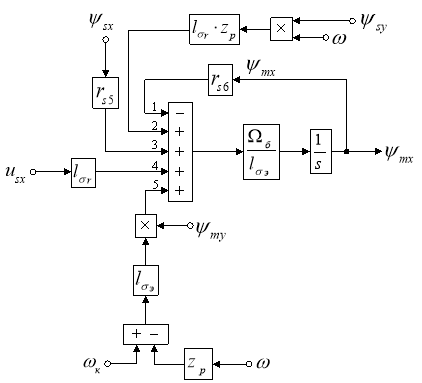
Рис. 3. Структурная схема для определения ψ_mx в Script-Simulink

Расчет коэффициентов будем производить в отдельном блоке Subsystem, поэтому вносим в структурную схему на рис. 3 блоки перемножения (рис. 4).

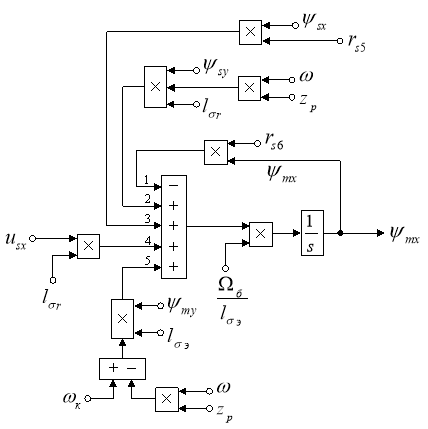
Рис. 4. Структурная схема для определения ψ_mx в Simulink

Аналогично, определим ψ_sy и ψ_my по оси (+j).

Из уравнения (15), полученного в работе [1], выразим ψ_sy:

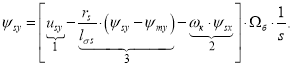
Структурная схема для определения ψ_sy представлена на рис. 5.

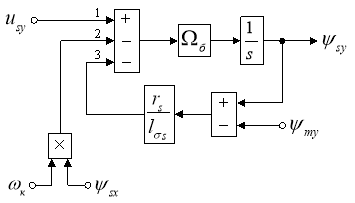
Рис. 5. Структурная схема для определения ψ_sy в Script-Simulink

Схема для расчета ψ_sy в Simulink приведена на рис. 6.

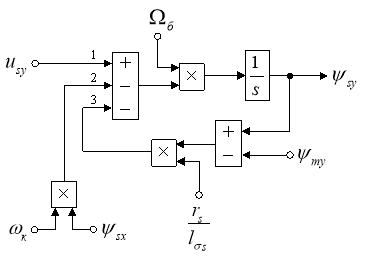
Рис. 6. Структурная схема для определения ψ_sy в Simulink

Для определения ψ_my приведем уравнение (16) из работы [1]:

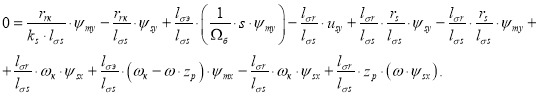
Перенесем слагаемое в левую часть и умножим обе части уравнения на :

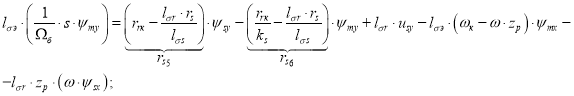
Отсюда ψ_my определится в следующей форме:

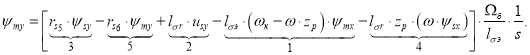
Структурная схема для определения ψ_my приведена на рис. 7.

Рис. 7. Структурная схема для определения ψ_my в Script-Simulink

Схема для расчета ψ_my в Simulink дана на рис. 8.

Рис. 8. Структурная схема для определения ψ_my в Simulink

На рис. 9 приведена структурная схема для реализации уравнения электромагнитного момента:

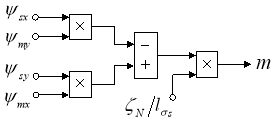
Рис. 9. Математическая модель определения электромагнитного момента m в Simulink

Из уравнения движения выразим механическую угловую скорость вращения вала двигателя (рис. 10):

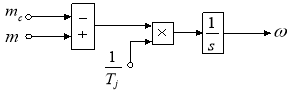
Рис. 10. Математическая модель уравнения движения в Simulink

Математическая модель асинхронного двигателя с короткозамкнутым ротором с переменными ψ_s – ψ_m на выходе интегрирующих звеньев в Simulink дана на рис. 11, …, 15.

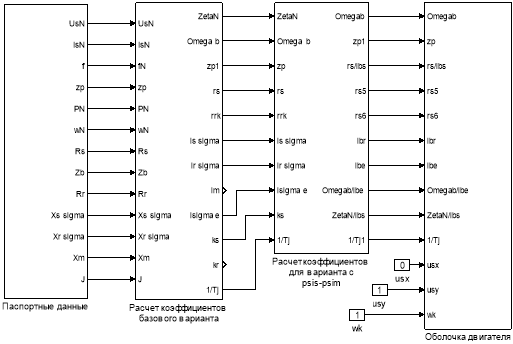
Рис. 11. Общая схема математической модели асинхронного двигателя с переменными ψ_s – ψ_m на выходе интегрирующих звеньев в Simulink

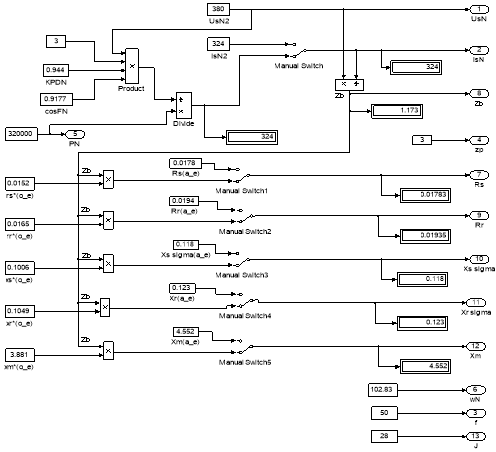
Рис. 12. Паспортные данные

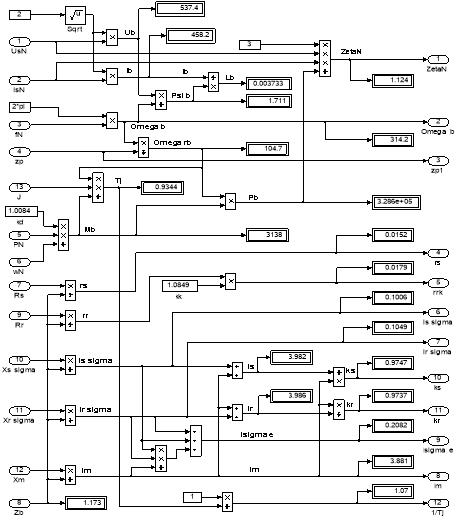
Рис. 13. Расчет коэффициентов базового варианта

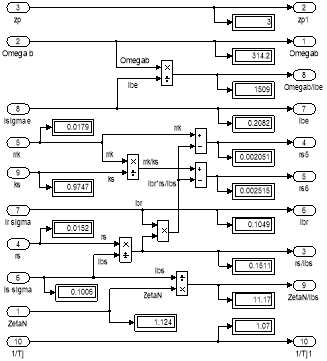
Рис. 14. Расчет коэффициентов для варианта с переменными ψ_s – ψ_m

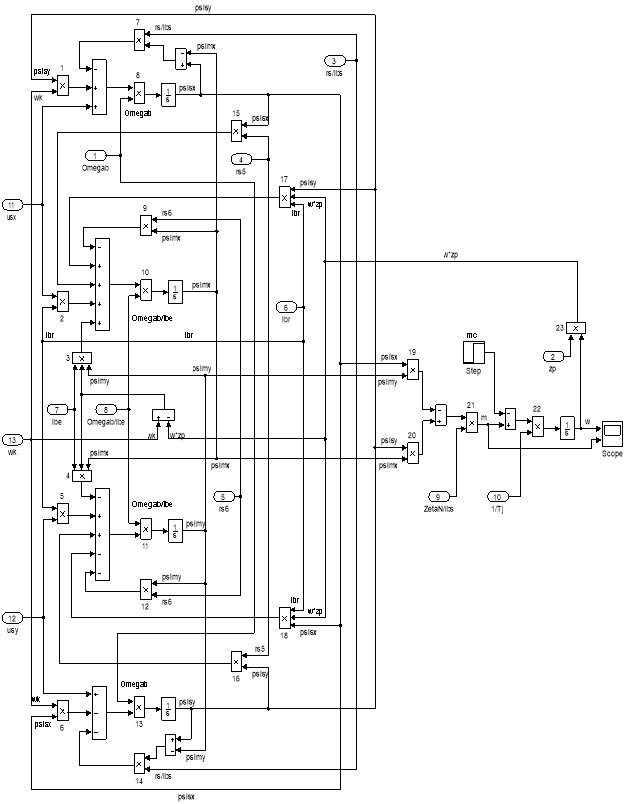
Рис. 15. Оболочка модели асинхронного двигателя с переменными ψ_s – ψ_m на выходе интегрирующих звеньев в Simulink

Эту же схему можно представить в более компактной форме с использованием блоков Goto и From (рис. 16) и отдельных субблоков с расчетами потокосцеплений, приведенных на рис. 17 и 18.

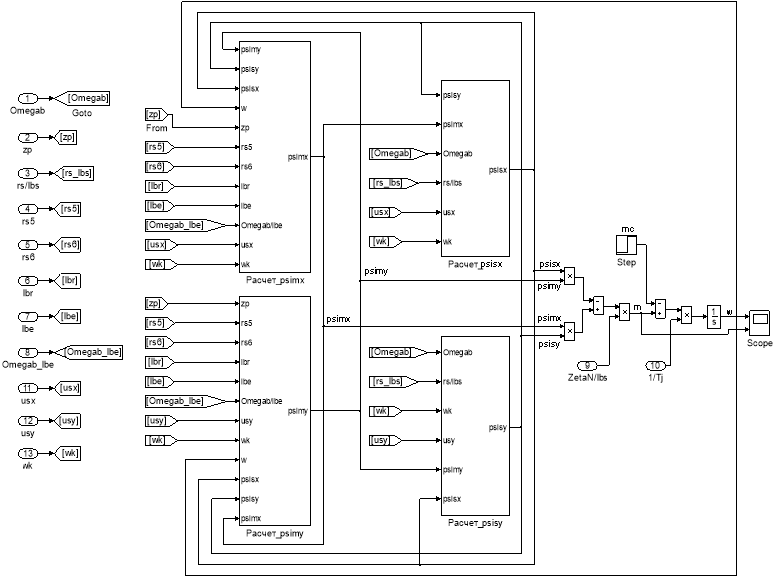
Рис. 16. Оболочка модели асинхронного двигателя с применением блоков Goto и From

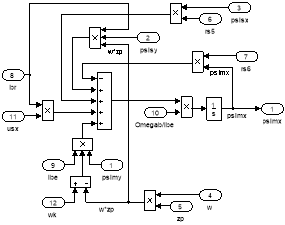
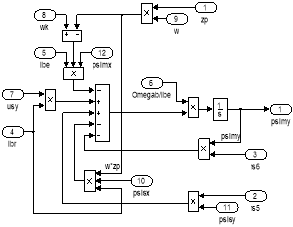
Рис. 17. Схемы для расчета ψ_mx и ψ_my

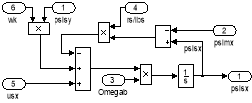
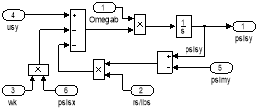
Рис. 18. Схемы для расчета ψ_sx и ψ_sy

В работах [2] и [3] дан образец расчета параметров асинхронного двигателя.

Номинальные данные:

Номинальный режим работыS1;

Номинальная мощность

Номинальное фазное напряжение

Номинальный фазный ток

Номинальная частота

Номинальная синхронная скорость

Номинальная скорость ротора

Номинальный КПД

Номинальный коэффициент мощности

Число пар полюсов

Параметры Т-образной схемы замещения при номинальной частоте:

Активное сопротивление обмотки статора

Индуктивное сопротивление рассеяния обмотки статора

Активное сопротивление обмотки ротора, приведенное к статору

Индуктивное сопротивление рассеяния обмотки ротора, приведенное статору

Главное индуктивное сопротивление

Суммарный момент инерции двигателя и механизма

Базисные величины системы относительных единиц:

Напряжение

Ток

Частота

Скорость ротора

Сопротивление

Потокосцепление

Индуктивность

Используя номинальные данные двигателя, определяем:

где – коэффициент, учитывающий различие значений электромагнитного момента и момента на валу двигателя в номинальном режиме (k_∆ = 1,0084).

В качестве базисной мощности выбираем значение электромагнитной мощности двигателя в номинальном режиме, определяемое по следующей формуле:

Относительные значения параметров схемы замещения двигателя:

Механическая постоянная времени:

Номинальное значение скольжения:

Относительное значение номинальной скорости ротора:

Нормирующий энергетический коэффициент:

При расчете режимов работы, для того чтобы i_sн = 1, m_N = 1, u_sN = 1, ω_sN = 1 и β_N = 0,018, необходимо откорректировать r_r:

где – корректирующий коэффициент [3, с. 296].

- коэффициент, показывающий отношение к .

Расчет коэффициентов для математической модели с переменными ψ_s – ψ_m:

Результаты моделирования асинхронного двигателя представлены на рис. 19.

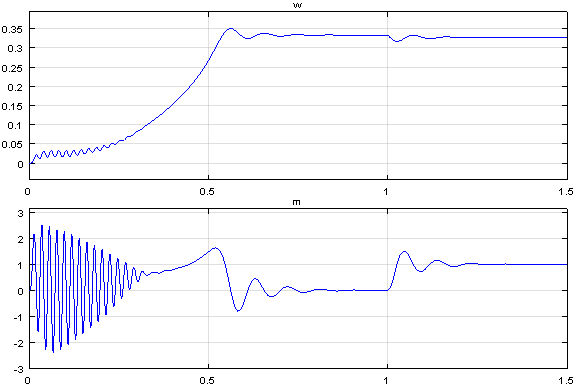
Рис. 19. Графики скорости и момента

Литература:

1. Емельянов А.А., Бесклеткин В.В., Пестеров Д.И., Юнусов Т.Ш., Воротилкин Е.А., Соснин А.С. Математическая модель асинхронного двигателя с переменными ψs – ψm на выходе апериодических звеньев в Simulink-Script // Молодой ученый. - 2017. - №8.
2. Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. – Екатеринбург: УРО РАН, 2000. - 654 с.
3. Шрейнер Р.Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р.Т. Шрейнер, А.В. Костылев, В.К. Кривовяз, С.И. Шилин. Под ред. проф. д.т.н. Р.Т. Шрейнера. - Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. - 361 с.