В статье рассмотрены методические аспекты факторного анализа, в частности рассмотрен на примере альтернативный вариант распределения «неразложенного» остатка в двухфакторной модели при методе «цепных подстановок».
Ключевые слова: факторный анализ, способ «цепных подстановок», альтернативный вариант распределения «неразложенного» остатка
Исследование основных факторов, закономерностей их взаимодействия и влияния на уровень результирующих параметров позволяет изучить состояние, эффективность функционирования, выявить имеющиеся резервы и основные направления дальнейшего развития экономики предприятий. Основным методом, позволяющим выявить закономерности развития экономики предприятий разного уровня, стал экономический анализ. Характерная и важнейшая особенность метода экономического анализа — изучение причин, вызвавших изменение тех или иных показателей производства. Поскольку экономические явления обусловлены причинными связями, то одной из основных задач экономического анализа является рассмотрение и изучение, исследование этих причин-факторов. Факторный анализ в экономике (и других науках) как метод исследования, основывается на предположении о наличии между изучаемым показателем и формирующими показателями причинно-следственной, детерминированной (функциональной) или стохастической взаимосвязи, которая может быть представлена в виде функции двух или более переменных, выраженной в явном виде. Разработка экономико-математических моделей на основе теоретических представлений взаимосвязях исследуемых показателей проводится путем логических построений, или с использованием статистических методов, например корреляционного и регрессионного анализа и их различных модификаций. При последующем факторном анализе полученных моделей используются различные способы оценки количественного воздействия отдельных факторов и их совокупного влияния на изучаемый результативный показатель (в абсолютных показателях или чаще в индексной форме). Одними из основных способов, являются способ обособленного изучения и способ последовательного расчета влияния факторов, или способ цепных подстановок. По способу обособленного изучения расчет количественного влияния изменения каждого фактора на изменение анализируемого показателя в отчетном периоде по сравнению с базисным не учитывает всех других факторов (они предполагаются неизменными). При этом сумма частных (по каждому фактору) изменений исследуемого показателя в общем случае количественно не совпадает с фактическим его приростом в отчетном периоде по сравнению с базисным.
При использовании способа цепных подстановок предполагается, что факторы влияют на изменение рассматриваемого показателя в строгой последовательности. Величина изменения рассматриваемого показателя под влиянием каждого следующего фактора определяется с учетом суммарного влияния изменения всех предыдущих факторов. В связи с этим количественная оценка влияния каждого отдельно взятого фактора при этом способе анализа зависит от принятой последовательности факторов. Арифметическая сумма пофакторных изменений при использовании способа цепных подстановок равна фактическому приросту результативного показателя в отчетном периоде по сравнению с базисным. По характеру взаимосвязей различают модели мультипликативные, в которых результативный показатель представлен произведением факторов аргументов и аддитивные, выраженные суммой (арифметической) факторов, и комбинированные из двух предыдущих типов. В мультипликативных моделях общий прирост исследуемого результативного показателя представляет собой алгебраическую сумму частных его приращений, обусловленных изменением факторов-аргументов и так называемого «неразложенного» остатка, который характеризуется как результат взаимодействия факторов. Например, в простейшей двухфакторной модели (зависимость стоимости товарной продукции Y от физического объема произведенной продукции q и оптовой цены p) прирост результативного фактора в отчетном периоде по сравнению с базисным (ΔQ= Q1 — Q0) в результате изменений объема продукции (Δq = q1 — q0) и оптовой цены (Δp = p1 — p0) соответствует выражению вида ΔQ= Q1 — Q0 = q1p1 — q0p0 = (q0 + Δq)(p0 + Δp) — q0p0 = Δqp0 + q0Δp + ΔqΔp. (1) В этом выражении два первых слагаемых характеризуют количественное влияние изменения отдельных факторов на изменение результативного показателя, как оно определяется по способу обособленного, изолированного изучения. Третье слагаемое является «неразложенным» остатком, на величину которого как раз и отличается сумма частных пофакторных изменений результативного показателя и фактическое его приращение в анализируемом периоде.
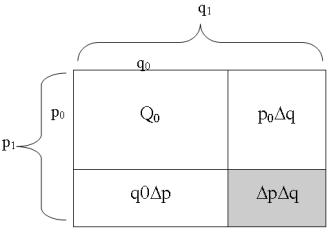
Для наглядности эти особенности можно представить в геометрической форме. Формально до сих пор нет единого мнения о методах распределения «неразложенного» остатка между факторами. Существует несколько методов анализа количественного влияния факторов на изменение результативного показателя:
‒ метод дифференциального исчисления («неразложенный» остаток в конечном счете отбрасывается, т. е. результат оценки соответствует получаемому по способу обособленного, изолированного изучения влияния факторов);
‒ индексный метод (не является самостоятельным, соответствует способу цепных подстановок; особенность только в том, что вместо абсолютных значений факторов используются их относительные величины);
‒ метод цепных подстановок (метод разниц);
‒ метод простого прибавления «неразложенного» остатка к результату обособленного влияния одного из факторов;
‒ метод взвешенных конечных разностей (при двухфакторной модели приводит к делению остатка между факторами поровну);
‒ логарифмический метод;
‒ метод коэффициентов (алгебраически неточен);
‒ метод дробления приращения факторов (путем деления всего интервала изменения факторов на возможно большее число равных малых отрезков);
‒ интегральный метод оценки факторных влияний.
Многие авторы считают бесперспективным поиск рациональных методов распределения «неразложенного» остатка, как не имеющий под собой теоретической базы. По методу цепных подстановок влияние отдельных факторов на результативный показатель применительно к приведенной выше двухфакторной модели стоимости товарной продукции может быть определено двумя вариантами способами:
ΔQ= Q1 — Q0 = Δqp0 + q1Δp;
ΔQ= Q1 — Q0 = q0Δp + Δqp1.
Основной проблемой способа цепных подстановок является обоснование порядка рассмотрения факторов, от которого зависит количественная оценка их влияния на результативный показатель. На текущий момент принято лишь единственное предложение по этому вопросу: что при оценке влияния изменения качественного показателя рекомендуется в качестве базы использовать данные отчетного (анализируемого) периода, а при рассмотрении объемного показателя — данные базисного периода.
В настоящее время эта рекомендация, не имеет строго научного обоснования, а при количестве факторов больше двух не может быть использована без группирования модели в двухфакторную, путем замены произведения нескольких факторов одним показателем. Более того, анализ показывает, что при использовании способа цепных подстановок оценка влияния первого фактора осуществляется так же, как и по методу обособленного рассмотрения факторов. Следовательно, оценка влияния второго фактора (q1Δp) будет равна сумме изолированного влияния этого фактора и «неразложенного» остатка, т. е. сумме второго и третьего слагаемых в выражении (1). Таким образом, при способе цепных подстановок, по существу, используется метод присоединения «неразложенного» остатка к одному из факторов, что на наш взгляд не даст точный результат анализа.
В предлагаемом варианте мы рассмотрим распределение «неразложенного» остатка пропорционально доли влияния каждого из факторов. Например: в базисном периоде было реализовано 100 ед.товара по цене 5 руб./ед., а в отчетном — 150 ед.товара по 7 руб./ед., тогда Q = pq, где Q — выручка, p — цена, q — количество товара соответственно. Данные, относящиеся к базисному периоду, обозначим «0», а относящиеся к отчетному периоду — «1». Тогда базисная выручка составит Q0=p0q0 = 100*5 = 500 (руб.), а отчетная выручка составит Q1=p1q1 = 150*7 = 1050 (руб.). Таким образом, выручка увеличилась на ΔQ = Q1 — Q0= 1050–500 = 550 (руб.) или iQ = Q1/Q0 = 1050/500 = 2,1 (раза). Исходя их классической двухфакторной индексной модели iQ = iqip, где iq = q1/q0, а ip= p1/p0. В нашем примере: iq = 150/100 = 1,5 и ip = 7/5 = 1,4, тогда iQ = 1,5*1,4 = 2,1.
Как видно из рисунка согласно классической двухфакторной модели два первых слагаемых характеризуют количественное влияние изменения отдельных факторов на изменение результативного показателя q0Δp = 100*2 = 200 (руб.); p0Δq = 5*50 = 250 (руб.) и третье слагаемое является «неразложенным» остатком, на величину которого как раз и отличается сумма частных пофакторных изменений результативного показателя и фактическое его приращение в анализируемом периоде ΔpΔq = 2*50 = 100 (руб.). Немного преобразуем эту составляющую:
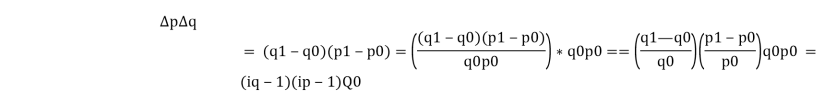
Определим долю влияния цены и количества, соответственно:
![]()
Доля изменения количества составила
![]()
Тогда получаем новые формулы для двухфакторного анализа:
![]()
![]()
Выполним элементарные математические преобразования.
![]()
![]()
В итоге:
ΔQp = (2,1*1,4–1,5)*500/(1,4+1,5) = 248,3 (руб.)
ΔQq = (2,1*1,5–1,4)*500/(1,4+1,5) = 301,7 (руб.)
ΔQ = 248,3 + 301,7 = 550 (руб.).
Предложенный подход факторного анализа позволяет устранить неоднозначность оценки влияния факторов и позволяет получать наиболее точный результат.
Литература:
- Адамов В. Е. Факторный индексный анализ (Методика и проблемы). М., 1977.
- Баканов М. И. Теория экономического анализа /М. И. Баканов, А. Д. Шеремет..,2000.
- Шеремет А. Д. Комплексный экономический анализ деятельности предприятий (вопросы методологии). М., 1974.
- Ф. Д. Ларичкин Методические подходы к факторному анализу изменений параметров горно-промышленного производства./ Научный журнал «Записки Горного института» т.208. СПб.,2014

