Данная работа посвящена анализу численных методов решения задач оптимального управления: метода последовательных приближений и метода вариации. Работа данных алгоритмов была апробирована на конкретном тестовом примере с известным аналитическим решением.
Ключевые слова: метод последовательных приближений, метод вариаций, оптимальное управление, фазовые ограничения
Проблеме численного решения задач оптимизации химико-технологических процессов уделяют особое внимание [1]. Во многих практических задачах правые части уравнений математической модели процессов имеют сложный вид, поэтому уравнения принципа максимума Понтрягина не всегда удается решить аналитически. Задача разработки или выбора наиболее эффективных численных алгоритмов в данном случае играет очень важную роль [2].
Пусть состояние физического процесса или объекта характеризуется переменными состояния (фазовыми координатами) 
. Физический процесс или динамика объекта описывается системой дифференциальных уравнений (уравнениями состояния):
(1)
где 
— функция, характеризующая управляющее воздействие, 
– время.
Задача оптимального управления заключается в определении функции управления 
в интервале 
которая обеспечивает экстремум (максимум и минимум) критерия качества, заданного в виде функционала:
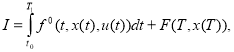(2)
и удовлетворяет ограничению:
(3)
где
— заданные непрерывно дифференцируемые функции [4].
Рассмотрим различные алгоритмы для решения задач оптимального управления.
Алгоритм метода последовательных приближений.
Задача оптимального управления (1) — (3) с помощью принципа максимума может быть сведена к решению краевой задачи системы дифференциальных уравнений 2n-го порядка.
Введем 
мерный вектор 
сопряженных переменных (импульсов) и функцию Гамильтона 
:
.(4)
Запишем сопряженную систему:
(5)
с граничными условиями:
.(6)
Согласно принципу максимума искомое оптимальное управление доставляет функции 
максимум по 
при любом 
, если 
и 
удовлетворяют системе (1) и граничным условиям (6).
Одним из наиболее распространенных методов решения указанной краевой задачи является метод последовательных приближений в пространстве управлений.
Задаем в качестве первого приближения некоторое допустимое управление 
, 
(выбор его может быть основан на каких-либо физических соображениях) и полагаем счётчик числа итераций равным 0.
Метод итерационный и 
итерация заключается в следующем:
-
Интегрируем управляемую систему с управлением
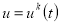до момента 
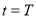. При этом определяется траектория 
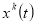и граничные условия для сопряженной системы.
-
Интегрируем сопряженную систему от момента
до 
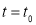при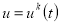 
, 
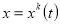— определяем сопряженные переменные 
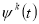на интервале 
.
-
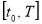Определяем новое приближение
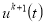на интервале 
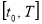из максимума функции 
:
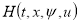(7)
-
Если условие (7) определяет
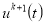неединственным образом, то выбираем любое из возможных значений. После этого переходим к следующей итерации и т. д.
Если процесс последовательных приближений сходится, то продолжаем его до тех пор, пока последующие приближения не будут отличаться друг от друга в пределах заданной точности [5]. Полученное после сходимости решение будет удовлетворять принципу максимума. Следует также отметить, что сходимость итерационного процесса существенно зависит от выбора первого приближения.
Алгоритм метода вариаций.
Положим, что известно некоторое управление 
, которое будем называть невозмущенным управлением.
В методе вариаций на каждой итерации вариация 
управления 
определяется путем минимизации линейной части приращения функционала 
, вызванного этой вариацией:
.
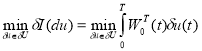Здесь 
– некоторая малая окрестность невозмущенного управления 
.
Общая схема метода вариаций в пространстве управлений:
-
Полагаем счётчик числа итераций
равным нулю и задаем начальное приближение к оптимальному управлению 
.
-
Решаем задачу Коши для системы дифференциальных уравнений (1) с управлением, полученным на предыдущем шаге — получаем фазовую траекторию
.
-
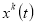Вычисляем
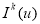— значение функционала качества (3) на невозмущенной траектории 
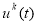. Запоминаем значение критерия и управление в достаточном числе точек.
-
В окрестности невозмущенной траектории
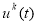выполняем линеаризацию задачи — вычисляем функциональную производную 
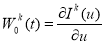и определяем окрестность 
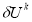невозмущенной траектории.
- Из условия
находим приращение 
управления 
-
Полагаем
.
-
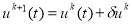Повторяем цикл с п.2 до тех пор, пока не выполнится условие
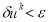[6].
Вычислительный эксперимент.
На основе созданных алгоритмов реализован программный комплекс на языке Object Pascal в среде Delphi [7-8], который включает возможности остановки процесса. При этом погрешности будут рассчитываться по евклидовой норме [9]:
Тестовый пример. Пусть управляемый процесс описывается системой дифференциальных уравнений:
(8)
с начальными условиями:
,
(9)
и следующими ограничениями на переменную времени:
(10)
и на управление:
(11)
Критерий оптимизации имеет вид
(12)
Требуется найти оптимальное программное управление 
и соответствующую ему траекторию 
, которые удовлетворяют уравнениям (8)-(9), ограничениям (10)-(11) и условию (12).
При отсутствии фазового ограничения оптимальное управление в задаче можно найти, используя принцип максимума для задачи со свободным правым концом.
Результат аналитического решения задачи представлен в работе [1].
В таблице 1 и представлен сравнительный анализ результатов численного решения задачи (8)-(12) методом вариации и методом последовательных приближений.
Полученные результаты показывают удовлетворительное согласование с аналитическим решением.
Таблица 1
Сравнительный анализ результатов решения задачи при точности вычислений 10-3
|
|
Начальное приближение |
Скорость вычислений, с |
Погрешность |
Значение функционала |
|||
|
|
|
|
|||||
|
Метод вариаций |
0,9 |
3,84 |
2,962 |
0,016 |
0,017 |
-3,996 |
|
|
Метод последовательных приближений |
0,9 |
0,54 |
0,998 |
1,419 |
1,419 |
-3,783 |
|
Литература:
- Григорьев И. В., Мифтахов Э. Н., Мустафина С. А. Математическое моделирование процесса полимеризации стирола с малеиновым ангидридом // Вестник технологического университета. 2015. Т. 18, № 15. С. 211-217.
- Григорьев И. В., Мифтахов Э. Н., Мустафина С. А. Математическое моделирование процесса полимеризации стирола с малеиновым ангидридом в гомогенной среде // В сборнике: Математическое и компьютерное моделирование естественно-научных и социальных проблем материалы X Международной научно-технической конференции молодых специалистов, аспирантов и студентов. Под редакцией И. В. Бойкова. 2016. С. 248-252.
- Григорьев И. В., Михайлова Т. А., Мустафина С. А. О численном алгоритме метода вариаций в пространстве управлений // Фундаментальные исследования. 2015. № 5-2. С. 279-283.
- Григорьев И. В., Мустафина С. А. Алгоритм глобальной оптимизации функций с использованием параллельных технологий. // Научный вестник. 2014. № 2 (2). С. 145-153.
- Григорьев И. В., Мустафина С. А. Нахождение оптимального программного управления методом вариации // Альтернативные источники энергии в транспортно-технологическом комплексе: проблемы и перспективы рационального использования. 2015. Т. 2. № 1. С. 254-257.
- Григорьев И. В., Мустафина С. А. Нахождение оптимального программного управления методом итераций // Путь науки. 2015. № 5 (15). С. 10-13.
- Шангареева Г. Р., Григорьев И. В., Мустафина С. А. Программное средство «SAOptimal» для решения задач оптимального управления // Хроники объединенного фонда электронных ресурсов Наука и образование. 2015. № 8-9 (75-76). С. 52.
- Григорьев И. В., Шангареева Г. Р., Мустафина С. А. Программный продукт «VarOptimalControl» решения задач оптимального управления // Хроники объединенного фонда электронных ресурсов Наука и образование. 2015. № 8-9 (75-76). С. 46.
- Григорьев И. В., Мустафина С. А. Реализация численного алгоритма решения задач оптимального управления с фазовыми ограничениями // Аспирант. 2015. № 5-1 (10). С. 49-51.
