В настоящее время цифровая аппаратура постепенно вытесняет аналоговую. Такую тенденцию можно описать многими факторами, но главный из них — простота обработки цифровых сигналов по сравнению аналоговыми. Поэтому цифровая обработка сигналов применяется в таких различных областях, как биомедицина, акустика, звуковая локация, радиолокация, сейсмология, связь, системы передачи данных, ядерная техника, и многих других. Для того, чтобы цифровая ЭВМ могла работать с аналоговым сигналом, его нужно преобразовать в цифровой вид, то есть сделать конвертацию. Конвертацию осуществляет специальное устройство — аналого-цифровой преобразователь. Такое преобразование содержит в себе погрешности, и тем она меньше, чем больше общая точность АЦП. В некоторых областях эти погрешности должны быть максимально минимизированы, то есть возникает вопрос подбора подходящего устройства. Поэтому каждый АЦП обладает рядом характеристик, отражающих его общую точность.
Характеристики АЦП подразделяются на статические, которые задают конечную точность преобразования, и динамические, характеризующие быстродействие данного класса устройств.
Но перед тем, как рассматривать статические характеристики, следует ввести определение передаточной характеристики. Итак, передаточная характеристика АЦП — это функция зависимости выходного кода АЦП от поданного напряжения. У идеального АЦП (у которого нет аппаратных погрешностей) такая зависимость представляет собой кусочно-линейную функцию из 
«ступеней», где 
— разрядность АЦП. Каждый горизонтальный отрезок этой функции соответствует одному из значений выходного кода. Если соединить линиями начала этих горизонтальных отрезков, то идеальная передаточная характеристика будет представлять собой прямую линию, проходящую через начало координат.
Рисунок 1 иллюстрирует идеальную передаточную характеристику для 3-х разрядного АЦП. Передаточная характеристика может быть реализована со смещением -1/2 LSB (см. рис. 2). Это достигается смещением передаточной характеристики влево. LSB (LeastSignificantBit) — наименьший значащий разряд или наименьшее значение напряжение, которое может быть измерено АЦП.
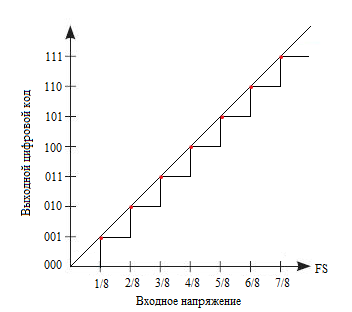
Рис. 1. Идеальная передаточная характеристика
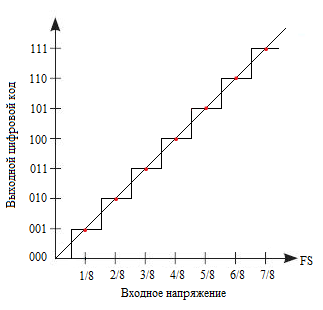
Рис. 2. Смещенная идеальная передаточная характеристика
Из-за технологического разброса параметров при изготовлении интегральных микросхем реальные АЦП не имеют идеальной передаточной характеристики. Отклонения от идеальной передаточной характеристики определяют статическую погрешность АЦП.
Статическая погрешность описывается следующими статическими характеристиками:
1) Аддитивная погрешность (погрешность смещения). Идеальная передаточная характеристика АЦП пересекает начало координат, а первый переход кода происходит при достижении значения 1/2 LSB (при несмещенной передаточной функции — 1 LSB). Аддитивная погрешность — смещение всей передаточной характеристики относительно идеальной, как показано на рис. 3.
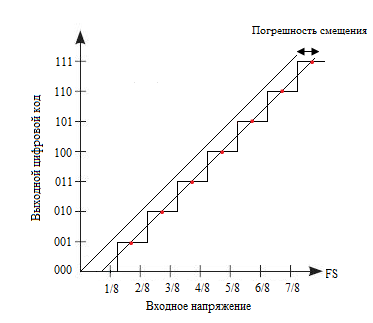
Рис. 3. Аддитивная погрешность
2) Мультипликативная погрешность (погрешность полной шкалы) представляет собой разность между идеальной и реальной передаточными характеристиками в точке максимального выходного значения при условии отсутствия смещения (см. рис. 4). Это проявляется как изменение наклона передаточной функции.
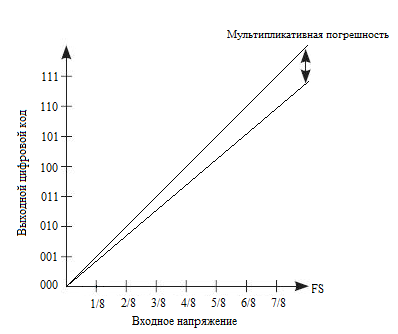
Рис. 4. Погрешность полной шкалы
3) Дифференциальнаянелинейность (Differential Non-Linearity). У идеальной передаточной характеристики АЦП ширина каждого уровня должна быть одинакова. Разница в длине горизонтальных отрезков этой кусочно-линейной функции из «ступеней» представляет собой дифференциальную нелинейность.Разность напряжений между каждым кодовым переходом должна быть равна величине 1 LSB. Отклонение этой разности от LSB определяются как дифференциальная нелинейность (см. рис. 5).
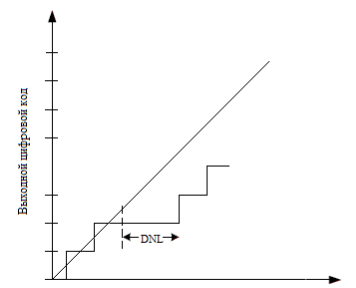
Рис. 5. Дифференциальная нелинейность
4) Интегральная нелинейность (IntegralNon-Linearity) — это погрешность, которая вызывается отклонением линейной функции передаточной характеристики АЦП от прямой линии, как показано на рисунке 6. Обычно передаточная функция с интегральной нелинейностью аппроксимируется прямой линией по методу наименьших квадратов. Часто аппроксимирующей прямой просто соединяют наименьшее и наибольшее значения. Интегральную нелинейность определяют путем сравнения напряжений, при которых происходят кодовые переходы. Для идеального АЦП эти переходы будут происходить при значениях входного напряжения, точно кратных 1 LSB. А для реального преобразователя такое условие может выполняться с погрешностью. Разность между «идеальными» уровнями напряжения, при которых происходит кодовый переход, и их реальными значениями выражается в единицах LSB и называется интегральной нелинейностью.
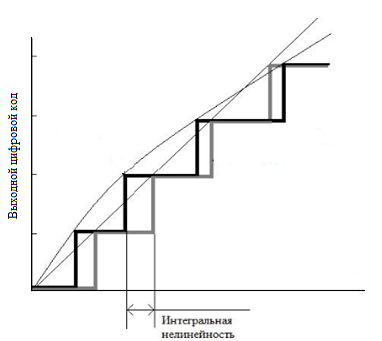
Рис. 6. Интегральная нелинейность
Для расчета интегральной и дифференциальной нелинейностей можно использовать гистограммный метод. Он заключается в том, что полученного цифрового сигнала вычисляются идеальное и реальное распределение кодов. Далее вычисляется их отношение. На рисунке 7 представлено распределение для реального шестиразрядного АЦП некоторого синусоидального сигнала.
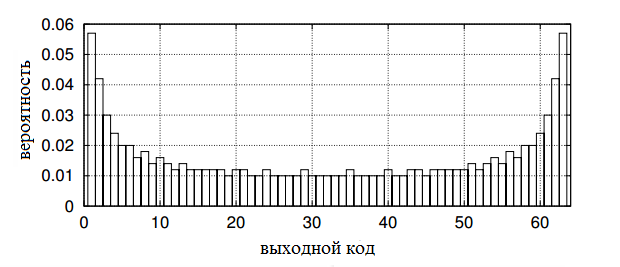
Рис. 7. Распределение кодов в реальном АЦП
Если бы тот же самый сигнал обрабатывался идеальным шестиразрядным АЦП, распределение кодов выглядело бы как показано на рисунке 8.
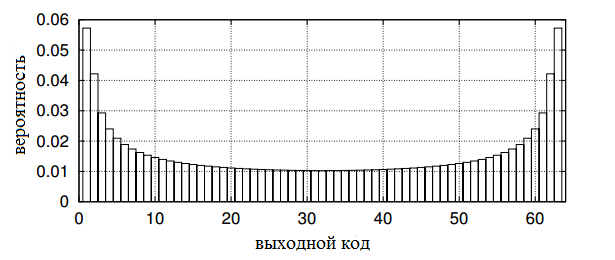
Рис. 8. Распределение кодов в идеальном АЦП
Идеальное распределение кодов для синусоидального сигнала выглядит следующим образом:
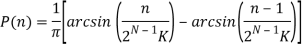
где:
— номер цифрового кода;
— разрядность АЦП;
.
Дифференциальная нелинейность рассчитывается по следующей формуле:
где:
— номер цифрового кода;
— количество отсчетов (длина выборки);
— вероятность распределения — го кода.
Интегральная нелинейность рассчитывается как:
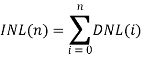
Следует отметить, что для использования гистограммного метода длина выборки должна быть большой. Существуют методики для получения нужного количества длины выборки:
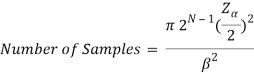
где:
— разрядность АЦП;
— ошибка измерения DNL в LSB;
— уровень доверия.
Общие значения для уровня доверия:
– 90 %: 1, 645;
– 95 %: 1, 96;
– 99 %: 2, 576.
Например, для оценки нелинейностей гистограммным методом 12-ти разрядного АЦП с = 0,1 (LSB) и уровнем доверия 95 % требуется 2471678 отсчетов. Для уровня доверия 99 % требуется 4269446 отсчетов.
Гистограммный метод — простой в использовании метод расчета нелинейностей АЦП. Его недостаток в том, что изначально требуется знать плотность распределения цифровых кодов. Кроме того, он не может похвастаться большой точностью.
Литература:
- Histogram Testing Determines DNL and INL Errors. Режим доступа: https://www.maximintegrated.com/en/app-notes/index.mvp/id/2085
- Как работают аналогово-цифровые преобразователи и что можно узнать из спецификации на АЦП. Режим доступа: http://www.efo.ru/doc/Silabs/Silabs.pl?2089
- Kent H. Lundberg. Analog-to-Digital Converter Testing.
