Современная постановка проблемы оптимизации формул приближенного интегрирования заключается в минимизации нормы функционала погрешности формулы на выбранных нормированных пространствах [1–3].
Рассмотрим кубатурную формулу общего вида
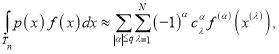(1)
над пространством С. Л. Соболева 
. Здесь соответственно 
и 
являются коэффициентами и узлами кубатурной формулы (1), 
— весовая функция, 
, 
— 
-мерный тор и 
— порядок обобщенных производных и 
.
Норма функции
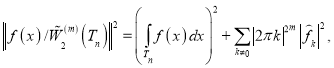(2)
Обобшенною функцию
(3)
назовем ее функционалом погрешности кубатурной формулы (1).
Справедлива следующая теорема.
Теорема 1.Квадрат нормы функционала погрешности (3) кубатурной формулы общего вида (1) над пространством
равен
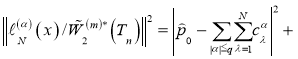
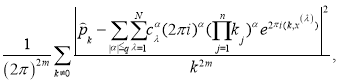
где 
— коэффициенты, 
— узлы кубатурной формулы (1) и 
— коэффициенты Фурье функции 
, т. е. 
.
Доказательство. Известно, что для функции 
справедливо следующее равенство: 
где 
, т. е. коэффициенты Фурье.
Таким образом, имеем
(4)
Здесь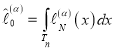 
, 
.
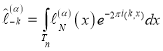Применяя к правой части (4) неравенство Коши-Шварца и учитывая (2) получим следующую оценку
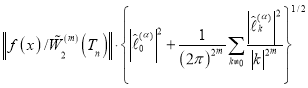(5)
Принимая во внимание (2)и (5), получим
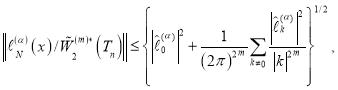(6)
где
(7)
Таким образом, имея ввиду(7) и (6) получим
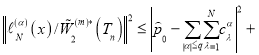
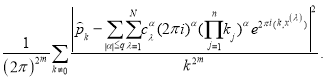(8)
Существует такая функция из 
, что в неравенстве (8) равенство достигается.
Действительно, рассмотрим следующую функцию 
:
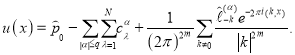
Вычисляя значение функционала 
на функцие 
получим
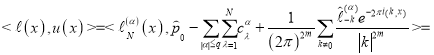
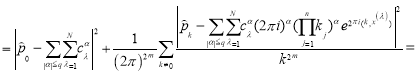
(9)
Учитивая (9),(6) получим доказательство теорема.
Введём обозначения 
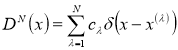, тогда для функционала погрешности кубатурной формулы (1) при 
имеет место следующая теорема, которая является основным результатом этой работы.
Теорема 2. Среди всех кубатурных формул вида (1) при
и 
,
оптимальная в пространстве 
является единственная формула с коэффициентами 
тогда, когда как узлы кубатурной формулы являются образом решетки на торе 
и коэффициенты которой равны между собой 
,
где
.
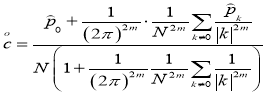Литература:
- Соболев С. Л. Введение в теорию кубатурных формул. М.: Наука, 1974. — 808с.
- Рамазанов М. Д. Лекции по теории приближенного интегрирования. Уфа, 1973. — 173с.
- Салихов Г. Н. Кубатурные формулы для многомерных сфер. Ташкент: Фан, 1985. — 104 с.
