В работе рассмотрены физические принципы и методы реализации фильтров оптического диапазона на основе плазмонных наноструктур и композиционных наночастиц FemOn-SiO2.
Ключевые слова: наноструктуры, плазмонный резонанс, оптическая фильтрация, биосенсорика
Наноструктуры с квантовыми точками дают уникальную возможность манипулировать светом на субволновом уровне, используя различные формы, такие как кубы [1,2], кластеры [3], оболочки [4], диски [6], пористые структуры [7,8], кольца [9], стержни [10] и наночастицы произвольной формы. Так же было представлено множество плазмонных устройств, включая модуляторы, интерферометры, переключатели, поляризаторы и поглотители [11,12]. Плазмонные структуры, используемые в качестве оптических фильтров обладают следующими преимуществам [13]: полоса пропускания перестраивается за счет изменения геометрических параметров и материалов наночастиц, фильтр способен функционировать в насыщенных влагой средах, таких как химические и биологические растворы, так как реакции между органическими растворами и металлическими наночастицами не проходят, невысокая себестоимость плазмонных фильтров в связи с технологией воспроизведения приборов, двумерный массив металлических наночастиц может быть использован в качестве высокоэффективного поляризационного фильтра в видимом диапазоне благодаря анизотропному отклику на электромагнитную волну.
Wu et al. продемонстрировал возможность создания плазмонного фильтра, основанного на метаматериалах, применимого для обработки сигналов в терагерцовом диапазоне. Реализация плазмонной структуры в терагерцовом диапазоне может привести к созданию ФВЧ для терагерцовых систем построения изображения [14]. Как толщина, так и период массивов металлических наночастиц обусловливают поверхностный плазмонный резонанс, соответственно влияя на поток фотонов. Fu et al. предложил плазмонный фильтр для видимого диапазона, основанный на массиве ромбических наночастиц серебра [13]. Однако, массив наночастиц треугольной формы, расположенных в вершинах шестиугольников обеспечивает более стабильную структуру и оптические свойства в отличие от массивов ромбических наночастиц серебра. Более того, чувствительность показателя преломления (RIS) сильно зависит от расположения, толщины и периода наномассивов.
Оптические фильтры на основе плазмонного резонанса вметаллических наночастицах
На рисунке 1 схематически изображен макроскопический объем металла (например, золота или серебра), подвергающийся оптическому облучению.
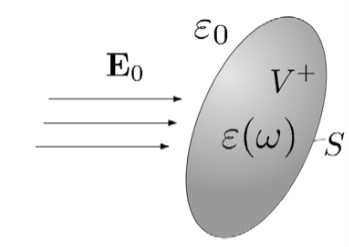
Рис. 1. Макроскопический объем металла, подвергающийся воздействию оптического излучения [15]
В данной ситуации никаких уникальных физических явлений не наблюдается. Однако, если размеры данного металлического объекта уменьшить и, в конечном счете привести к наномасштабным, то наночастица под воздействием оптического излучения может начать излучать, резонировать и оказаться мощным наноразмерным локализованным источником света. Подобные локализованные источники излучения применимы в различных областях науки и технологии, таких как сканирующая ближнепольная оптическая микроскопия [6], нанолитография [12], биосенсорика [14], рамановская спектроскопия (SERS) [13], нанофотоника [14].
Эксперименты показывают, что металлические (золотые и серебряные) наночастицы могут проявлять резонансные свойства на определенных частотах, при которых выполняются следующие условия: диэлектрическая проницаемость наночастицы отрицательная, длина волны, распространяющейся в свободном пространстве, велика по сравнению с размерами наночастицы.
Последнее условие, очевидно, предполагает, что резонанс по своей природе электростатический. Если диэлектрическая проницаемость частицы отрицательная, то теорема единственности электростатики не выполняется. По этой причине, могут появляться беззарядовые электростатические поля для определенных отрицательных значений диэлектрической проницаемости. Соответствующие беззарядовые электрические поля отвечают резонансным плазмонным модам.
Необходимо отметить, что плазмонный резонанс в металлических наночастицах — физическое явление, обусловленное наноразмерными масштабами, поскольку два условия резонанса (отрицательная диэлектрическая проницаемость и малость частицы по сравнению с длиной волны) могут быть одновременно реализованы в наномасштабе.
Возникает вопрос о корректности применения термина «диэлектрическая проницаемость» применительно к металлическим наночастицам, подвергающимся воздействию оптического излучения. Причина состоит в том, что электроны проводимости в металлических наночастицах «закрепляются» оптическим излучением и осуществляют осциллирующие колебания около некоего положения равновесия. В таком случае, электроны проводимости невозможно отличить от связанных зарядов в диэлектриках. Именно поэтому металлические наночастицы ведут себя на оптических частотах подобно диэлектрикам с дисперсией. Последнее означает, что диэлектрическая проницаемость зависит от частоты. Для определенного диапазона частот вещественная часть диэлектрической проницаемости может принимать отрицательные значения. Для металлов этот диапазон частот приходится на их плазмонную частоту, где соотношение дисперсии полностью определяется взаимодействием между электромагнитным излучением (светом) и электронами проводимости. Для хороших проводников (таких как серебро или золото), плазмонные частоты находятся в видимом диапазоне, что объясняет применение серебряных и золотых наночастиц для изучения плазмонного резонанса и практических применений.
Важно отметить, что плазмонный резонанс имеет место не только в металлических наночастицах, но и на любых наночастицах, диэлектрическая проницаемость которых проявляет дисперсию, принимающую отрицательные значения. Одним из примеров служит карбид кремния (SiC) отрицательная диэлектрическая проницаемость которого обусловлена не взаимодействием электронов проводимости со светом, а специфическими свойствами вибраций кристаллической решетки в полярных кристаллах [15].
Как уже было упомянуто ранее, второе условие — малость размеров наночастицы по сравнению с длиной волны падающего света — раскрывает физическую природу плазмонного резонанса в наночастицах как электростатический резонанс. Действительно, вследствие этого условия гармонические электромагнитные поля в пределах и вблизи наночастиц изменяются практически синфазно. Как результат, в любой момент времени эти поля могут быть рассмотрены как электростатические. Электростатическая природа плазмонного резонанса в наночастицах и их отрицательная диэлектрическая проницаемость предполагают усиление локальных электрических полей внутри наночастиц и поблизости от них. На рисунке 2 изображена сферическая наночастица с отрицательной диэлектрической проницаемостью ε, подвергающейся воздействию однородного внешнего поля E0. Поскольку ε < 0, вектор поляризации P направлен противоположно E0, чтоприводит к образованию поверхностных электрических зарядов, создающих «деполяризующее» поле E´, сонаправленное E0. Это приводит к увеличению суммарного электрического поля E = E0 + E´ внутри сферической наночастицы.
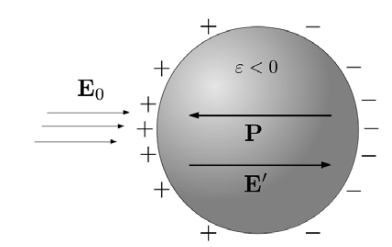
Рис. 2. Сферическая наночастица с отрицательной диэлектрической проницаемостью, подвергающаяся воздействию внешнего электрического поля [15]
Частота плазмонного резонанса в металлических наночастицах не зависит от размера самой наночастицы (при выполнении условия малости размера частицы по сравнению с длиной волны падающего излучения). Такая инвариантность относительно размера подразумевает, что в случае массива почти одинаковых по форме, но разных по размерам металлических наночастиц они могут резонировать на практически одинаковых длинах волн. Следовательно, плазмонный резонанс может быть одновременно возбужден на всех наночастицах сразу.
Формулировка задачи на собственные значения для плазмонного резонанса позволяет напрямую рассчитать отрицательные значения диэлектрической проницаемости на которых происходит плазмонный резонанс. Эти отрицательные значения диэлектрической проницаемости могут быть использованы для любого дисперсионного соотношения конкретного сорта наночастиц с целью определить соответствующие частоты плазмонного резонанса. Таким образом, свойства плазмонного резонанса, определяемые формой наночастиц могут быть полностью отделены от свойств, зависящих от дисперсионного соотношения. Другими словами, решение задачи на собственные значения плазмонного резонанса для наночастицы определенной формы может быть использовано для различных материалов этой наночастицы с целью нахождения резонансных частот.
Изучение возбуждения плазмонных мод падающим светом и эффекты омических потерь и потерь на излучение показывает, что дипольные плазмонные моды возбуждаются падающим излучением, создаваемым удаленными источниками. Это утверждение справедливо, поскольку электрическое поле этого излучения практически однородно в области нахождения наночастицы в связи с малостью размеров наночастицы по сравнению с длиной волны падающего света.
Падающее излучение наиболее эффективно взаимодействует с плазмонной модой, если дипольный момент этой моды параллелен направлению электрического поля падающего излучения. Анализ возбуждения плазмонных мод также показывает, что качество плазмонного резонанса, то есть локальное усиление падающего оптического излучения, можно контролировать, изменяя отношение между вещественной частью диэлектрической проницаемости к ее мнимой части на частоте резонанса. Для золота и серебра соотношение наиболее приемлемо, когда длина волны излучения, распространяющегося в свободном пространстве находится в пределах от 650–1000 нм и 600–1400 нм соответственно (рисунок 3 а, б) [16].
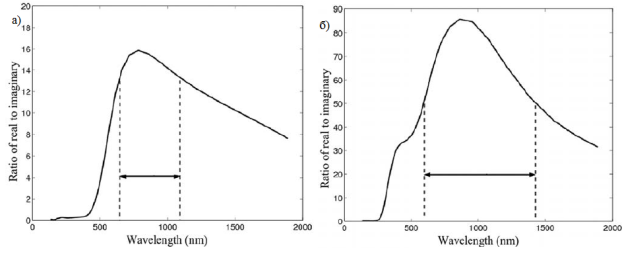Рис. 3. Зависимость отношения между вещественной частью диэлектрической проницаемости к ее мнимой части для золота а) и серебра б) [16]
Таким образом, плазмонный резонанс в золотых и серебряных наночастицах может быть возбужден наиболее эффективно на соответствующих диапазонах частоты. Из рисунка 3 видно, что отношение между вещественной частью диэлектрической проницаемости к ее мнимой части значительно выше для серебра, чем для золота. Этот фактор особенно важен для поверхностного рамановского рассеяния (SERS), где для экспериментов прежде всего используются наночастицы серебра (хотя окисление серебра представляет некоторые трудности).
Оптические фильтры на основе композиционных магнитных наночастиц FemOn-SiO2
Последние двадцать лет ферромагнитные жидкости являлись объектом интенсивного исследования в первую очередь благодаря возможности коммерческого применения в различных областях [17], в том числе непроницаемые герметики, радиаторы для громкоговорителей и трансформаторов, вязкие демпферы, сепараторы, чернила на основе магнитных жидкостей, актюаторы, датчики ускорения и позиционирования, контрастирующий агент для наблюдения кровотока в неинвазивных измерениях. [2] Также ферромагнитные жидкости широко применяются при исследованиях фундаментальных физических явлений. Эмульсии, основанные на ферромагнитный жидкостях используются в качестве модельной системы для изучения природы коллоидальных взаимодействий [18]. Вышеупомянутые исследования обеспечили понимание условий стабилизации коллоидных суспензий, что, в свою очередь, привело к развитию областей применения эмульсий ферромагнитных жидкостях: детектирование дефектов в ферромагнитных компонентах и материалах [7].
Ферромагнитные жидкости могут быть использованы при создании полосовых фильтров в оптическом диапазоне [19]. Существует три основных типа оптических фильтров: оптический ФНЧ (фильтр низких частот), оптический ФВЧ (фильтр высоких частот) и оптический ПФ (полосовой фильтр). Оптические ФНЧ используются в качестве заграждающих при флуоресценции, поскольку обеспечивают прохождение эмитированного при флуоресценции света, задерживая сигнал возбуждения. Оптические ФВЧ применяются для фильтрации сигнала возбуждения. Такие фильтры, разработанные для спектроскопии, называются спектроскопическими фильтрами.
Оптические ПФ пропускают свет только в определенной полосе длин волн шириной от менее одного до десятков нанометров. Такие фильтры применяются в широком диапазоне научно-производственных областей, включающих спектрофотометрию, медицинскую диагностику, химический анализ, колориметрию и астрономию. При использовании в спектрофотометрии оптические ПФ предпочтительнее монохроматоров в связи с лучшим коэффициентом пропускания и отношение сигнал-шум.
Магнитные наночастицы получены по двух стадийной методике. Изначально, золь был приготовлен при растворении тетраэтоксисилана (TEOS) в изопропаноле. Содержание TEOS менялось от 20 до 80 об. % После добавления гидрированного аммиака произошла золь-гель реакция. Затем, осадок был высушен при комнатной температуре и подвергся отжигу при температуре 300оС в течение 15 минут для получения ксерогеля. Ксерогель подвергся ультразвуковому воздействию в водных растворах Fe3+ и Fe2+. Гидрированный аммиак был добавлен в смесь для инициации реакции:
Рис. 4. РЭМ-изображение наночастиц магнетита, стабилизированных олеиновой кислотой. [20]
В ходе реакции были образованы большие скопления наночастиц, осажденные в течение нескольких часов. Осаждение не происходит в растворах, включающих ксерогель SiO2 независимо от их состава. В этом случае растворы оставались стабильны по крайней мере 30 дней. Осажденные наночастицы были промыты дистиллированной водой с целью удалить растворимые в воде соли аммония. Седиментация под действием силы тяжести оказалась пренебрежимо мала.[1]
На рисунке 5 представлен результат математической обработки спектров оптического поглощения коллоидного раствора FemOn-SiO2 при концентрации TEOS 60 vol. %. Исследования ряда композиционных структур, содержащих нанокристаллиты TiO2 [21] позволяют связать существование полос с образованием наноструктур различного размера. Согласно теории G.Mie [22], представляется возможным моделировать полосу поглощения композиционной системы за счет изменения геометрических размеров агломератов FemOn на поверхности SiO2 (что, в свою очередь, позволяет использовать данную систему в качестве режектирующего фильтра в оптическом диапазоне):
(1)
где 
— максимальный коэффициент поглощения, 
— полуширина полосы поглощения (см-1), 
эВ/мм — оптическая константа, 
— радиус коллоидных частиц, n — число частиц в единице объема.
Оценочный радиус кластеров, полученный по этой формуле, 
1.9 нм, 1.8 нм и 2.07 нм соответственно для полос поглощения кластеров, 28488 см-1, 27275 см-1, 29536 см-1 (при концентрации TEOS 60 об. %) [3].
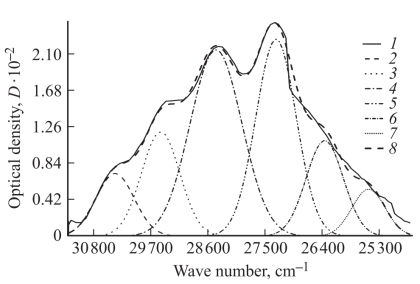
Рис. 5. Результат разложения спектра оптического поглощения коллоидного раствора FemOn-SiO2 при концентрации TEOS 60 vol. % на гауссовы составляющие: 1 — исходный спектр поглощения; полосы поглощения, характеризующиеся положениями максимумов, cm−1; 2–30480, 3–29530, 4–28480, 5–27300, 6–26220, 7–25130, 8 — результат суммирования полученных полос поглощения [3]
Заключение
Продемонстрирована принципиальная возможность построения фильтров оптического диапазона на основе поверхностного плазмонного резонанса в металлических наночастицах.
Композиционные магнитные наночастицы FemOn-SiO2 исследованы методом спектроскопии оптического поглощения с использованием теории G. Mie. Обнаружены шесть полос поглощения, связанных с образованием на поверхности пористой матрицы SiO2 конгломератов FemOn шести характерных размеров. На основании полученных экспериментальных данных предложен метод реализации фильтров режектирующего типа.
Статья посвящается памяти профессора, д.ф.-м. наук Бочаровой Татьяны Викторовны.
Литература:
1. H. J. Chen, Z. H. Sun, W. H. Ni et al., Nano resonance in (gold core)-(dielectric shell) nanostructures without symmetry breaking // Small, vol. 5, pp. 2111–2119, 2009
2. X. Kou, Z. Sun, Z. Yang et al Curvature directed assembly of gold nanocubes, nanobranches, and nanospheres // Langmuir, vol. 25, no. 3, pp. 1692–1698, 2009.
3. Р. С. Смердов, Т. В. Бочарова, В. С. Левицкий, К.Г и др. Спектроскопические свойства гамма-облученных композитных наночастиц FemOn-SiO2 //ФТТ, Т.58, № 5, с.892–896, (2016).
4. J. B. Lassiter, J. Aizpurua, L. I. Hernandez et al. Close encounters between two nanoshells // Nano Letters, vol. 8, no. 4, pp. 1212–1218, 2008.
I. Zoriґc, E. M. Larsson, B. Kasemo et al, Localized surface plasmons shed light on nanoscale metal hydrides //Advanced Materials, vol. 22, no. 41, pp. 4628–4633, 2010.
5. Y. J. Liu, Y. B. Zheng, J. Liou et al, All-optical modulation of localized surface plasmon coupling in a hybrid system composed of photoswitchable gratings and au nanodisk arrays //The Journal of Physical Chemistry C, vol. 115, no. 15, pp. 7717–7722, 2011.
6. T. W. Ebbesen, H. J. Lezec, H. F. Ghaemi et al, Extraordinary optical transmission through sub-wavelenght hole arrays // Nature, vol. 391, no. 6668, pp. 667–669, 1998.
7. Y. J. Liu, E. S. P. Leong, B. Wang et al, Optical transmission enhancement and tuning by overylaying liquid crystals on a gold film with patterned nanoholes, //Plasmonics, vol. 6, no. 4, pp. 659–664, 2011.
A. R. Halpern and R. M. Corn Lithographically patterned electrodeposition of gold, silver, and nickel nanoring arrays with widely tunable near-infrared plasmonic resonances // ACS Nano, vol. 7, no. 2, pp. 1755–1762, 2013.
8. H. Chen, L. Shao, Q. Li et al, Gold nanorods and their plasmonic properties, //Chemical Society Reviews, vol. 42, no. 7, pp. 2679–2724, 2013.
9. J. A. Dionne, K. Diest, L. A. Sweatlock et al, PlasMOStor: a metal-oxide-Si field effect plasmonic modulator // Nano Letters, vol. 9, no. 2, pp. 897–902, 2009.
10. Y. K. Gao, Z. M. Xin, Q. Q. Gan et al, Plasmonic interferometers for label-free multiplexed sensing //Optics Express, vol. 21, no. 5, pp. 5859–5871, 2013.
11. Y. Q. Fu, S. L. Zhu, X. L. Zhou et al, Rhombic silver nanoparticles array-based plasmonic filter // International Journal of Modern Physics B, vol. 25, no. 19, pp. 2557–2566, 2011.
12. M. Lubecke, K.Mizuno, G. M. Rebeiz, Micromachining for terahertz applications // IEEE Transactions on Microwave Theory and Techniques, vol. 46, no. 11, pp. 1821–1831, 1998.
I. D. Mayergoyz, Plasmon Resonances in Nanoparticles, World Scientific Publishing Co. Pte. Ltd., 325 (2013).
13. P. B. Johnson and R. W. Christy, Physical Review B 6, 4370 (1972).
14. Основы золь-гель технологии нанокомпозитов / Максимов А. И., Мошников В. А., Таиров Ю. М., Шилова О. А.
15. СПб: Лань, 2008, 304 с.
16. И. Е. Кононова, К. Г. Гареев, В. А. Мошников и др Самосборка фрактальных агрегатов системы магнетит-диоксид кремния в постоянном магнитном поле, //Неорг. Матер. том 50, № 1, с. 1–7. 2014
17. John Philip et al. A tunable optical filter // Measurement Science and Technology, 14, 1289–1294, (2003)
18. К. Г. Гареев, В. В. Лучинин, В. А. Мошников, Магнитные наноматериалы, получаемые химическими методами, // Биотехносфера. № 5(29), с.2–13, (2013).
19. S. D. Stookey. USA Pat. 2920971, 1960.
20. L. Gao, T. J. Vadakkan, V. Nammalvar. Nanoshells for in vivo imaging using two-photon excitation microscopy //Nanotechnology 22, 36, 365 102 (2011).
[1] Синтез образцов выполнен ассистентом К. Г. Гареевым
