Механические характеристики полимеров в большой степени определяются их химической и надмолекулярной структурами. Причем предельные механические характеристики волокон в основном лимитируются характеристиками аморфной фазы [1]. Но аморфная фаза определяет и специфические полезные свойства волокон - гибкость, прочность в узле, стойкость к многократным изгибам. Поэтому является актуальной проблема получения полимеров с требуемой структурой. При этом встает проблема исследования и количественного описания структуры полимеров, включающая задачи выбора параметров, характеризующих структуру полимера, методов определения данных параметров, заданных значений данных параметров, обеспечивающих заданные характеристики полимера, связи режимных параметров техпроцесса с параметрами структуры и т.д.
Для исследования структуры полимеров и химических волокон широко применяются методы рентгеновского анализа, термомеханического анализа, электронной микроскопии, двойного лучепреломления, инфракрасный дихроизм, экспресс методы на основе исследования ползучести и другие методы. Но данные методы часто не позволяют получить количественные характеристики структуры полимеров.
Большими возможностями в исследовании структуры аморфной фазы, играющей решающую роль в формировании механических характеристик полимеров, обладает метод релаксационной спектрометрии [1-3]. Метод основан на двух положениях физики твердого тела [1,2]:
- каждая система состоит из подсистем, слабо взаимодействующих друг с другом, и в целом функция распределения времен релаксации полимера состоит из дискретного спектра дельта-функций,
- времена релаксации структурных элементов зависят от температуры, давления и активационного характера молекулярной подвижности структурных единиц.
Метод заключается в снятии экспериментальных кривых релаксации внутреннего напряжения полимера после нанесения ступенчатого воздействия по удлинению (рис. 1) и разложении кривой изменения напряжения во времени на сумму экспоненциальных составляющих ![]() ,
,
параметры которых ![]() (соответственно, модуль упругости, время релаксации) и являются характеристиками компонент сетки полимера.
(соответственно, модуль упругости, время релаксации) и являются характеристиками компонент сетки полимера.
Начальная амплитуда![]() определяет вес данной компоненты в графике напряжения (в структуре полимера) волокна, а постоянная времени
определяет вес данной компоненты в графике напряжения (в структуре полимера) волокна, а постоянная времени![]() характеризует время жизни данной компоненты.
характеризует время жизни данной компоненты.
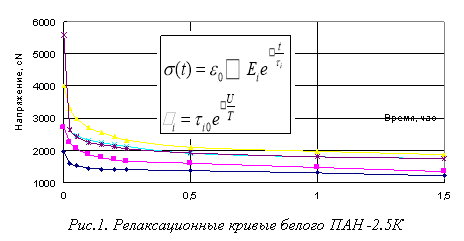
В данной работе идентификация релаксационной модели ПАН волокна производится в 2 этапа. На первом этапе методом последовательного логарифмирования [1,4] определяются количество составляющих экспонент (количество релаксационных составляющих структуры) и начальные оценки коэффициентов (начальные амплитуды и постоянные времени).
Суть метода последовательного логарифмирования (метода Симою) заключается в возможности выделения из экспериментальной релаксационной кривой отдельных релаксационных компонент.
Общая экспериментальная кривая равна сумме экспонент. Но время затухания компонент различное. Следовательно, на последнем участке экспериментальная кривая содержит только одну экспоненту с максимальным временем жизни (например, компоненту с параметрами ![]() ). При логарифмировании экспериментальной кривой последний участок является логарифмом от данной экспоненты и превращается в прямую линию:
). При логарифмировании экспериментальной кривой последний участок является логарифмом от данной экспоненты и превращается в прямую линию:
![]() .
.
По последнему участку прологарифмированной кривой находим параметры первой релаксационной компоненты и вычитаем эту компоненту ![]() из экспериментальной кривой релаксации. По аналогичному алгоритму находим 2-ю, 3-ю и последующие компоненты и оценки их параметров.
из экспериментальной кривой релаксации. По аналогичному алгоритму находим 2-ю, 3-ю и последующие компоненты и оценки их параметров.
На втором этапе нелинейного программирования [5] производится уточнение оценок параметров модели. При этом методом численной оптимизации (метод сопряженных градиентов, метод Ньютона) производится минимизация суммы квадратов отклонений расчетных значений напряжений от экспериментальных на множестве релаксационных параметров:
![]()
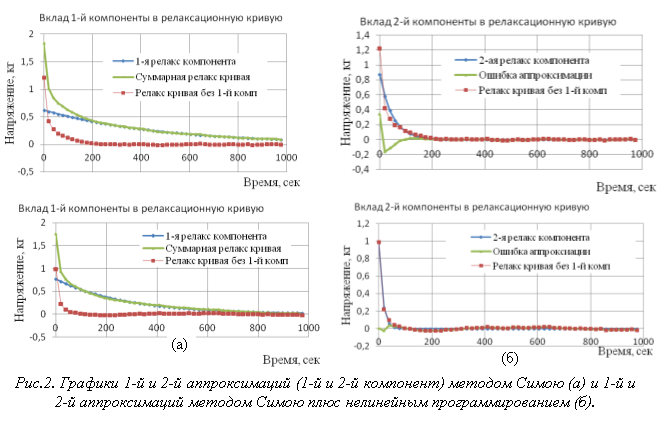
Предлагаемый метод реализован в электронной таблице Excel. На рисунке 2(а,б) представлены графики 1-й и 2-й аппроксимаций (1-й и 2-й компонент) методом Симою. Затем оценки параметров релаксационных компонент были уточнены методом нелинейного программирования. На рисунке 3 приведены графики экспериментальных, расчетных значений кривых релаксации и ошибок аппроксимации для методов последовательного логарифмировании (а) и с последующим уточнением параметров методом нелинейного программирования (б). Полученные оценки параметров и показатели адекватности сведены в таблице 1. Критерий во втором случае имеет меньшее значение.
![]()
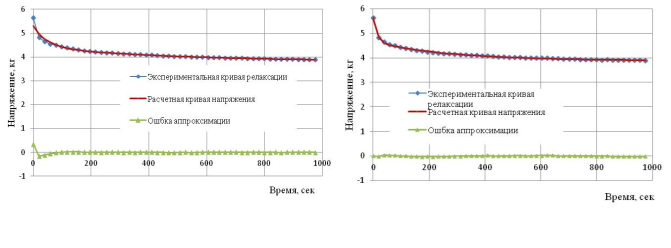
Таблица 1
|
№№ п/п |
Параметр |
1-я компонента |
2-я компонента |
Критерий МНК | ||
|
С1 |
а1=1/1 |
С2 |
а2=1/2 | |||
|
1 |
Оценки по методу Симою |
0,621 |
500 |
0,873 |
48,07 |
0,1627 |
|
2 |
Оценки по методу Симою и НП |
0,767 |
280,82 |
0,982 |
13,9 |
0,0112 |
В результате получено две экспоненциальных составляющих с параметрами С1 = 0,767 сн/т, С2 =0,982 сн/т (начальные значения экспонент) и постоянными времени 1/a1 = 280,82 сек, 1/a2 = 13,9 сек. Здесь же приведено значение критерия МНК SS = 0,0112 (сн/т)2.
Результатами работы является:
1. В Excel разработана таблица, позволяющая в диалоговом режиме производить построение модели релаксации химического волокна методом последовательного логарифмирования с последующим уточнением оценок методом нелинейного программирования.
2. Разработанная система может быть использована для идентификации структурных моделей полимеров на основе релаксационных характеристик.
Литература:
- Бартенев Г.М. Структура и релаксационные свойства эластомеров. М. Химия, 1979, 288с.
- Бартенев Г.М., Бартенева А.Г. Релаксационные свойства полимеров. М.: Химия, 1992, 384с.
- Тобольский А. Структура и свойства полимеров. М. Химия. 1964.-324с.
- Дудников Е.Д., Балакирев В.С. и др. Построение математических моделей химико-технологических объектов. Л. Химия, 1970, 312 с.
- Химмельблау Д. Прикладное нелинейное программирование. М. Мир, 1975, 536с.

