)

С момента зарождения резиновой промышленности, большое внимание уделяется проблеме использования отходов производства и потребления, в том числе изношенных резинотехнических изделий. Одним из путей повышения эффективности производства РТИ, улучшения экологичности производства, снижения себестоимости продукции является использование измельченных резиновых вулканизатов в резиновых смесях [1,2].

В данной работе приводится анализ релаксационных характеристик резины 57-7024-110 на основе этиленпропиленового каучука.

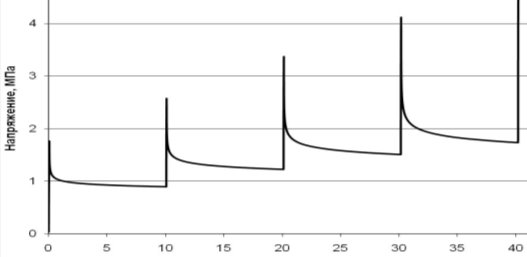
На рис. 1 приведен график изменения напряжения вулканизован­ной резины 57-7024-110, полученные при многошаговой вытяжке (удлинении) (по 50% на каждом шаге) при температуре 25°С с выдержкой на каждом шаге в течение 10 минут для прохождения релаксации. Как можно видеть, при увеличении времени наблюдения имеет место снижение равновесного напряжения. Следовательно, при описании дли­тельных процессов можно вместе с упругой составляющей напряжения ис­пользовать дополнительную максвелловскую компоненту. На графиках можно выделить, на каждом шаге релаксации, две составляющие напряжения: релаксирующую составляющую , изменяющуюся на j пе­риоде релаксации, и равновесную , остающуюся неизменной на текущем периоде релаксации. Графики также показывают изменение параметров релаксации с увеличением деформации, что выражается в возрастании напряже­ния (>) и увеличении времени релаксации (>) на последующих шагах вытяжки. На основании этого для описания релаксации напряжения принята модель, включающая параллельно работающие n элементов Мак­свелла и один упругий элемент [3, 4]. Значение n определяется необходимой точностью описания. Для учета изменения релаксационных процессов в процессе деформации модель имеет переменные параметры. При принятой релаксационной модели резины общее напряжение полимера (σ(t)) является суммой напряжений релаксирующей (σр(t)) и равновесной составляющих (σ∞(t)):    ∞(t)

Свободные составляющие решения уравнений Максвелла:

, i = 1,2,...n

где - вязкость, модуль упругости i элемента, - время релаксации, при ступенчатом изменении деформации описывают напряжения релаксации каждого элемента(): , i = 1,2,...n

где - начальное напряжение i-того элемента после осуществления ступенчатого воздействия.

Полное релаксирующее напряжение () равно сумме напряжений эле­ментов Максвелла:

Равновесное напряжение (σ∞(t))описывается линейным уравнением по закону Гука:      σ∞(t)=E(ε)·ε(t)      где: Е(ε)- модуль упругого элемента, значение которого зависит от вели­чины деформации.

Последовательное описание релаксационных кривых одной, двумя и тремя максвелловскими компонентами с одним упругим элементом, показало достаточность использования двух компонент (корреляционное отношение 0,996).

Время, мин

Рис.1. Напряжение образца при 50% вытяжке

Исследование изменения релаксационных параметров резины при деформации проводилось путем анализа изменения параметров релакса­ционной модели (ГОСТ 270-75 тип 1). Для каждого шага релаксации проводили математическое описание изменения напряжения и подбирали такие параметры релаксаторов, чтобы расчетные кривые напряжения по квадратичному критерию максимально приближались к экспериментальным. Оценки начальных напряжений (, ), времен релаксации максвелловских компонент (,) и модуля упругого элемента (σ∞) приведены в табл.1.

Таблица 1

Параметры релаксационных моделей

Следует отметить достаточно выраженную зависимость ре­лаксационных параметров от деформации. Закономерности изменения параметров максвелловских элементов совпадают - модули элементов с увеличением деформации повышаются по зависимостям второго порядка, времена релаксации, несколько увеличиваясь, выходят на постоянные значения. Как и ожидалось, введение порошка, хотя и снижает физико-механические свойства, но резиновая смесь 57-7024-110 достаточно хорошо держит напряжение, что сказывается на ее большой наполняемости. После введения технологической добавки ВЦ-20КП физико-химические параметры резиновой смеси улучшаются.

Выводы: показано, что параметры релаксации и их изменения позволяют описать изменение механических характеристик при деформации и пред­ложить гипотезы об изменении структуры резины, в том числе, вулканиза­ционной сетки при больших деформациях. Результаты работы предназначены для учета изменения характери­стик резины при моделировании напряженно-деформированного состоя­ния изделий, исследования связи состава резиновой смеси и технологических па­раметров процесса с релаксационными и механическими характеристика­ми резины, для построения системы управления технологическим процес­сом.

Литература:

1.    Перлина Ж. В., О влиянии резиновой крошки на свойства шинных резин /Ж. В. Перлина, Д. Р. Разгон //Сборник докладов XI международной научно-практической конференции «Резиновая промышленность. Сырье. Материалы. Технологии», М.: НИИШП, 2005. - С. 204-206.

2. Применение мелкодисперсного резинового этиленпропиленового порошка в составе резиновых смесей на основе этиленпропиленовых каучуков / Адов М. В. и [др.] // Каучук и резина. - 2009. - №6. - С. 32-34.

3. Анализ релаксационных характеристик резины / Сочнев А.Н. и [др.] // Сборник докладов XII симпозиума «Проблемы шин и резинокордных композитов», М.: НИИШП, 2006, С. 178-184.

4. Бартенев, Г. М. Структура и релаксационные свойства эластомеров / Г. М. Бартенев – М.: Химия, 1979. – 288 с.