Организация учебного исследования в начальной школе «Много ли секретов у треугольника». Организация предметной тематической недели в 4 классе

Данная методическая разработка поможет учителям начальных классов организовать учебно-исследовательскую деятельность на уроках математики или организовать внеурочную деятельность в рамках предмета математика. Эта работа написана в помощь учителям начальных классов, которые используют в своей практике инструменты ОТСМ-ТРИЗ, но и будет полезна и интересна другим педагогам, организующим на своих уроках исследовательскую деятельность. В работе дано описание проведенной тематической недели в 4 классе по изучению секретов треугольника с методическими рекомендациями, где и как организовать учебно-исследовательскую деятельность и примеры результатов деятельности учеников.

 

Одним из важнейших механизмов реализации Требований к результатам освоения основной образовательной программы начального общего образования (далее ООП НОО) являются планируемые результаты освоения предметных программ и междисциплинарных программ. Именно «планируемые результаты уточняют и конкретизируют Требования стандарта к результатам освоения основных образовательных программ для каждого учебного предмета». В связи с этим актуальным становится вопрос о том, как можно формировать универсальные учебные действия, «действий обеспечивающих школьникам способность к саморазвитию и самосовершенствованию… «ключевую компетенцию, как умение учиться».

Многие учителя начальных классов понимают важность умения учиться и поддерживают идеи концепции развития универсальных учебных действий, но всё же испытывают определенные трудности в организации образовательного процесса с учетом системно-деятельностного подхода ориентированного на достижения планируемых результатов как предметных, так и метапредметных. Именно последние вызывают большую трудность, именно здесь большое количество вопрос возникает у педагогов. Одной из основных причин наряду с недостаточностью знаний в области планируемых результатов можно считать и недостаток знаний и умений в области применения таких современных образовательных технологий, которые позволяют организовать деятельностный образовательный процесс младших школьников. А ведь именно через грамотно организованную учебную, учебно-творческую, учебно-практическую, учебно-исследовательскую деятельность идет формирование универсальных учебных действий.

Идея проведения данной недели (серии уроков), выросла благодаря обучению на дистанционном курсе «Мастерские знаний» (сайт http://jlprojmoodle.org/) и изучению работ Т. Н. Журавлёвой «Исследовательская работа «Определение площади треугольника» [2] в 4-м классе» и Г. В. Беловой «Конструкторский набор для проведения исследовательских проектов по математике в 5–6 классах основной школы» [1].

Традиционно в начальной школе проводятся предметные недели, в рамках данных недель ребята рисуют, решают различные предметные ребусы, кроссворды и викторины, устраивают предметные праздники. А что, если данную неделю провести с нацеливанием на достижение планируемых результатов и провести как тематическую? Так и «родилась» неделя «треугольника». Организация учебно-исследовательской деятельности младших школьников в данной форме поможет формированию некоторых личностных, регулятивных, познавательных и коммуникативных универсальных действий не только на базовом уровне, но и на повышенном.

Личностные универсальные учебные действия:

в результате работы у учащихся будут сформированы:

-        учебно-познавательный интерес к новому учебному материалу и способам решения новой частной задачи;

-        учащиеся получать возможность для формирования:

-        выраженной устойчивой учебно-познавательной мотивации учения;

-        устойчивого учебно-познавательного интереса к новым общим способам решения задач.

Регулятивные универсальные учебные действия:

ученик научится:

-        принимать и сохранять учебную задачу;

-        планировать своё действие в соответствии с поставленной задачей;

-        ученик получит возможность:

-        преобразовывать практическую задачу в познавательную;

-        проявлять познавательную инициативу;

-        самостоятельно адекватно оценивать правильность выполнения действий и вносить необходимые коррективы.

Познавательные универсальные учебные действия:

ученик научится:

-        использовать модели и схемы для решения задач;

-        ориентироваться на разнообразие способов решения задач;

-        осуществлять анализ объектов и синтез;

-        проводить сравнение и классификацию по заданным критериям;

-        устанавливать причинно-следственные связи;

ученик получит возможность научиться:

-        создавать и преобразовывать модели и схемы для решения задач;

-        строить логическое рассуждение, включающее установление причинно-следственных связей;

-        произвольно и осознанно владеть общим приемом решения задач.

Коммуникативные универсальные учебные действия:

ученик научится:

-        учитывать разные мнения;

-        формулировать собственное мнение;

-        договариваться и приходить к общему решению совместной деятельности;

ученик получит возможность научиться:

-        учитывать разные мнения и интересы и обосновывать собственную позицию;

-        задавать вопросы, необходимые для организации собственной деятельности и сотрудничества;

-        адекватно использовать речь для планирования и регуляции своей деятельности.

Эта работа написана в помощь учителям начальных классов, которые используют в своей практике инструменты ОТСМ-ТРИЗ, но и будет полезна и интересна другим педагогам, организующим на своих уроках исследовательскую деятельность. В работе дано описание проведенной тематической недели в 4 классе по изучению секретов треугольника с методическими рекомендациями, где и как организовать учебно-исследовательскую деятельность и примеры результатов деятельности учеников.

День первый. Создание и освоение копилки треугольников. Паспорт треугольника

На данном уроке через тренинг «Да-Нет» определяем тему недели (рис. 1).

Учитель загадывает математический объект, изображенный на доске (в данном случае загадан треугольник). Дети должны разгадать его, задавая вопросы, на которые можно отвечать только «Да», «Нет» или «Не имеет значения». Пример диалога:

Дети: — Этот объект содержит числа?

Учитель: — Нет.

Дети: — Это плоская фигура?

Учитель: — Да.

Дети: — У нее есть углы?

Учитель: — Да.

Дети: — Число углов больше четырех?

Учитель: — Нет.

И т. д.

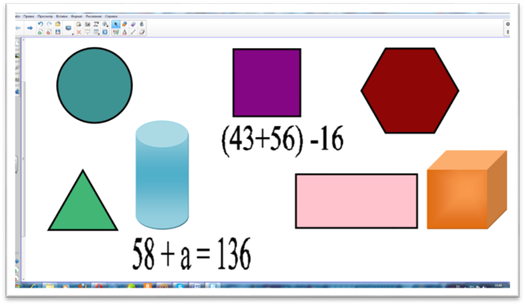
Рис. 1. Копилка для игры «Да-Нет»

 

Тренинг «Теремок».

Для проведения игры дети разбирают картинки с изображением различных геометрических фигур и геометрических тел. Первый объект, который поселяется в «Теремок» — это треугольник. В «Теремок» пускают жить, только те объекты, которые скажут, чем они похожи на треугольник. Условие — признаки повторять нельзя, надо находить новые (в «Теремок» может поселиться, практически любой объект, например, прямоугольник — тоже имеет углы, цилиндр — треугольник плоский, а цилиндр тоже имеет плоскую поверхность и т. п.).

Практическая работа. Учащиеся чертят и вырезают из бумаги свой вариант треугольника. После чего, задача ребят попробовать объединиться в группы по видам треугольников по соотношению сторон и по величине угла. В результате будут: равносторонние, равнобедренные, разносторонние треугольники; прямоугольные, тупоугольные и остроугольные треугольники.

Учащиеся заполняют паспорт своего конкретного треугольника — таблица 1 (основа взята из работы Т. Н. Журавлевой [2]).

Таблица 1

 

Домашнее задание. Начертить и вырезать из картона три вида треугольников (либо по величине угла, либо по соотношению сторон).

День второй. Вычисление периметров и площадей треугольников. Определение суммы углов треугольников

Работа с копилкой треугольников, которая раздается детям.

Тренинг «Мои друзья». Учитель называет признак, по которому он собирает «друзей», дети, имеющие треугольник с соответствующим признаком, выходят к доске. Здесь можно сначала брать в друзья треугольники по одному признаку (равносторонние, тупоугольные и т.д), а затем усложнить задание. Например, «мои друзья» — прямоугольные равнобедренные треугольники, тупоугольный равнобедренный треугольник, прямоугольный равносторонний треугольник. (Данные признаки позволяют поставить проблемные вопросы: «А может ли быть прямоугольный треугольник равносторонним?», «Бывает ли тупоугольный треугольник равнобедренным или равносторонним?» и т. д.).

Далее проводится поисковая работа по выводу формул периметра и площади треугольника [2].

Работа в группах. Нахождение площади и периметра треугольников. Учащиеся выбирают треугольники для работы. Две группы — по соотношению сторон, две группы по величине угла, а одна группа выбирают треугольники, у которых есть два (равнобедренный прямоугольный треугольник, тупоугольный равнобедренный например) Находят периметр и площадь данных треугольников, данные заносят в таблицу 2 (учащиеся уже знают, как находить площадь треугольников разного вида).

Таблица 2

 

Для дальнейшей работы задаем детям вопросы: — Почему в одном столбце у нас вопросительный знак? Что мы можем ещё вычислить у треугольника? (Можем найти сумму углов треугольника).

Учащиеся продолжают работать в группах, измеряют углы треугольников и находят сумму углов каждого треугольника, данные заносят в таблицу.

Делаем вывод: Сумма углов любого по виду треугольника равна 180 градусам.

День третий. Вывод суммы углов многоугольника

Моделируем из треугольников многоугольники (четырехугольники, пятиугольники, шестиугольники, семиугольники и т. д. — рис. 2).

Чертим треугольник, затем дорисовываем до четырехугольника при помощи ещё одного треугольника. Измеряем углы и находим сумму углов. Данные заносим в таблицу (3). Достраиваем до пятиугольника, шестиугольника. Условие одно — достроить следующий многоугольник можно только при помощи треугольника.

Рис. 2. Составление многоугольников из треугольников

 

Таблица 3

 

Дальше одно группа детей находит сумму углов у четырехугольников разного вида, другая у пятиугольников, шестиугольников (рис. 3).

Рис. 3. Вычисление суммы углов многоугольника

 

Вывод: Сумма углов у многоугольников увеличивается на 180 градусов с увеличением на один угол у многоугольника.

День четвертый. Вывод закономерностей

Работа в группах.

1.               Прямоугольные разносторонние треугольники.

2.               Равносторонние треугольники.

3.               Равнобедренные тупоугольные треугольники.

4.               Равнобедренные прямоугольные треугольники.

5.               Разносторонние тупоугольные треугольники.

Цель работы: измерить стороны и углы и вывести закономерность. Все данные учащиеся заносят в таблицу 4 и по наблюдениям делают вывод. Затем каждая группа делится своей работой. Моделируют свой вывод (таблица 5).

Таблица 4

 

Таблица 5

 

Возможные выводы, которые могут сделать учащиеся и модели выводов:

1.                 Если треугольник равнобедренный прямоугольный, то два других угла острые по 45 градусов. Если у треугольника два угла по 45 градусов, то это равнобедренный прямоугольный треугольник (рис. 4).

Рис. 4. Наблюдение за равнобедренным прямоугольным треугольником

 

Рис. 5. Наблюдение за равносторонним треугольником

 

1.                  Если треугольник равносторонний, то все углы острые и равны 60 градусам. Если у треугольника все углы острые по 60 градусов, то это равносторонний треугольник (рис. 5).

2.                  Если треугольник прямоугольный разносторонний, то два другие угла НЕРАВНЫЕ острые и в сумме равны 90 градусам. Если два угла НЕРАВНЫЕ острые и в сумме дают 90 градусов, то это прямоугольный разносторонний треугольник (рис. 6).

Рис. 6. Наблюдение за прямоугольным разносторонним треугольником

 

1.                  Если треугольник разносторонний тупоугольный, то два другие углы НЕРАВНЫЕ острые в сумме меньше 90 градусов. Если сумма двух НЕРАВНЫХ острых углов в треугольнике меньше 90 градусов, то это тупоугольный разносторонний треугольник (рис. 7).

Рис. 7 Наблюдение за разносторонним тупоугольным треугольником

 

1.                  Если треугольник равнобедренный тупоугольный, то сумма двух одинаковых углов меньше 90 градусов. Если сумма двух одинаковых углов меньше 90 градусов, то это равнобедренный тупоугольный треугольник (рис. 8).

Рис. 8. Наблюдение за равнобедренным тупоугольным треугольником

 

Домашнее задание. Нарисовать рисунок или сделать аппликацию, используя геометрические фигуры.

Примеры работ:

 

День пятый. Правильные пирамиды

В начале урока показать презентацию про египетские пирамиды. (Чтобы продолжить работу, можно задать вопрос — «Почему ребятам показали пирамиды?»).

Можно просто показать изображения пирамид и попросить связать с темой нашей недели. (Равнобедренный треугольник является гранью пирамиды).

Помним, что египетские пирамиды — это четырехугольные пирамиды, но могут быть и треугольные и многоугольные пирамиды. Мы будем изучать только правильные пирамиды. В основании таких пирамид находятся правильные многоугольники. Об это дети должны сделать вывод в результате работы.

Работу строим на копилке пирамид, которые даны детям. (Копилку можно дать всем одинаковую в каждую группу, а можно в одну группу дать треугольные пирамиды, в другую четырехугольную, пятиугольную.) Дети считают, сколько граней у пирамиды, измеряют грани, смотрят, что находится в основании, делают вывод о многоугольнике в основании. По ходу работы заполняют таблицу 6.

Таблица 6.

 

Дети в результате работы делают вывод, что если в основании пирамиды треугольник, то граней у пирамиды три, если четырехугольник, то граней четыре и т. д. Также они делают вывод, что у многоугольника, который находится в основании пирамиды, все стороны равны, он правильный. По окончании работы дают учащиеся называют, что нужно знать, чтобы сами построить свою правильную пирамиду. 1 — в основании правильный многоугольник, длина стороны которого равна длине стороны равнобедренного треугольника, который является гранью пирамиды. Все грани пирамиды одинаковые, количество их зависит от угольника в основании.

Практическая работа.

Изготавливаем свою правильную пирамиду. Здесь можно работать в группе, а можно в парах, но можно и индивидуально. Так как неделя подходит к концу, то может целесообразно изготовить индивидуальную пирамиду, на гранях, которой написать все секреты треугольника, которые дети раскрыли за время работы.

Вспоминаем, как начертить равнобедренный треугольник. (Чертим основание, делим его пополам, проводим прямую линию под прямым углом и соединяем одинаковые ребра треугольника). Готовую разметку и размеры пирамиды не даем, пусть дети изготовят самостоятельно свою пирамиду. При первом изготовлении они будут использовать отдельные детали, а не разметку. (А вот потом на уроках технологии можно уже будет вспомнить, как чертили разметку для куба, параллелограмма и попробовать начертить разметку для пирамиды.)

Итог недели. Выставка пирамид с секретами. Примеры работ:

 

Литература:

 

1.      Белова Г. В. Конструкторский набор для проведения исследовательских проектов по математике в 5–6 классах основной школы / http://jlproj.org/this_bibl/Belova_constr+.pdf

2.      Журавлева Т. Н. Исследовательская работа «Определение площади треугольника» в 4-м классе / http://jlproj.org/this_bibl/Jur_tr.pdf

3.      Нестеренко А. А. Мастерская знаний: проблемно-ориентированное обучение на базе ОТСМ-ТРИЗ. Учебно-методическое пособие для педагогов / М., BookInFile, 2013.