Наглядная геометрия
Автор: Шмелева Ольга Владимировна
Рубрика: Спецвыпуск
Опубликовано в Школьная педагогика №2 (9) июнь 2017 г.
Дата публикации: 27.04.2017
Статья просмотрена: 2120 раз
Библиографическое описание:
Шмелева, О. В. Наглядная геометрия / О. В. Шмелева. — Текст : непосредственный // Школьная педагогика. — 2017. — № 2.1 (9.1). — С. 67-72. — URL: https://moluch.ru/th/2/archive/60/2418/ (дата обращения: 24.04.2024).

Вид деятельности: познавательная
Форма: кружок
Направление воспитания: творческое, сознательное отношение к своему образованию
Направление развитие личности: общеинтеллектуальное
Пояснительная записка
Я думаю, что никогда до настоящего времени
мы не жили в такой геометрический период.
Все вокруг — геометрия.
Французский архитектор Ле Корбюзье
Геометрия дает учителю уникальную возможность развивать ребенка на любой стадии формирования его интеллекта. Три ее основные составляющие: фигуры, логика и практическая применимость позволяют гармонично развивать образное и логическое мышление ребенка любого возраста, воспитывать у него навыки познавательной, творческой и практической деятельности.
Первая ступень изучения — интуитивная — основана на системе общих представлений о фигурах (свойствах, классах, действиях и т. д.). Иначе эту ступень можно рассматривать как визуальную (наглядную), а систему представлений — как набор образов, готовых к актуализации в повседневной жизни, творчестве, познавательной деятельности, в частности в дальнейших более серьезных занятиях геометрией.
Выделение особого “интуитивного” пропедевтического курса геометрии, нацеленного на укрепление и совершенствование системы геометрических представлений, с одной стороны, способствует предварительной адаптации учащихся к регулярному курсу геометрии, с другой — может сформировать достаточный уровень геометрических знаний в гуманитарном секторе школьного образования.
Данная программа является актуальной, так как обеспечивает интеллектуальное развитие, необходимое для дальнейшей самореализации и формирования личности обучающегося. Кроме того, программа «Наглядная геометрия» направлена на помощь школьникам в изучении геометрии и подготовке к успешной сдачи модуля «Геометрия» на ОГЭ и ЕГЭ по математике.
Курс «Наглядная геометрия» рассчитан на два года — 5 и 6 классы, 2 часа в неделю, 68 часов в каждом классе, всего 136 часов. Ежегодно изучается как планиметрический, так и стереометрический материал.
Целью курса «Наглядная геометрия» является организация творческой, интеллектуально-практической, проектно-исследовательской деятельность учащихся, направленной на развитие пространственных представлений, образного мышления, изобразительно-графических умений, приемов конструктивной деятельности, геометрической интуиции, обучение правильной геометрической речи и познавательного интереса учащихся.
Задачи:
– продолжить формирование геометрического стиля мышления;
– создать представление об основных фигурах и понятиях школьного курса геометрии;
– ознакомить с новый геометрической терминологией;
– продолжить формирование элементарных навыков изображения геометрических фигур;
– начать обучение правильной геометрической речи;
– вырабатывать навыки пользования чертёжными и измерительными инструментами;
– развивать пространственное воображение, глазомер;
– развивать творческие способности;
– прививать настойчивость в достижении цели;
– воспитывать трудолюбие, творческое и ответственное отношение к выполняемой работе.
Таблица 1
Учебно-тематический план
|
№п\п |
Тема |
Количество часов |
Форма проведения |
|
5 класс |
|||
|
Плоскостное моделирование |
35 |
||
|
|
Первые шаги в геометрии |
13 |
Рассказ учителя, беседа, творческая лаборатория, геометрический бой, проект, геометрический практикум, тест |
|
|
Фигуры на плоскости |
8 |
Творческая лаборатория, геометрический бой, игра «Геометрическое лото», проект |
|
|
Площади многоугольников |
10 |
Рассказ учителя, беседа, геометрический бой, проект, геометрический практикум, игра «Что это такое?» |
|
|
Топологические опыты |
4 |
Творческая лаборатория |
|
Объемное моделирование |
33 |
||
|
|
Прямоугольный параллелепипед, куб |
11 |
Рассказ учителя, беседа, творческая лаборатория, геометрический бой, геометрический практикум |
|
|
Призмы |
6 |
Графическая работа геометрический практикум |
|
|
Пирамида |
4 |
Творческая лаборатория |
|
|
Метод трёх проекций |
2 |
Графическая работа |
|
|
Правильные многогранники |
5 |
Графическая работа, геометрический практикум |
|
|
Организация и проведение конструкторских проектов |
5 |
Экскурсия, творческая лаборатория, проект |
|
Всего |
68 |
||
|
6 класс |
|||
|
Плоскостное моделирование |
40 |
||
|
|
Неравенство треугольника |
2 |
Беседа, геометрический практикум |
|
|
Поворот, симметрия |
14 |
Рассказ учителя, беседа, графическая работа, геометрический бой, игра «Испорченный телефон»,проект |
|
|
Параллельность и перпендикулярность прямых |
3 |
Геометрический диктант |
|
|
Координаты на плоскости |
7 |
Творческая лаборатория, графическая работа, игра «Рисуем в координатах», проект |
|
|
Графы, кривые |
5 |
Творческая лаборатория, графическая работа |
|
|
Окружность. Геометрическое место точек |
9 |
Творческая лаборатория, геометрический бой, геометрический практикум |
|
Объёмное моделирование |
28 |
||
|
|
Пирамида |
4 |
Рассказ учителя, беседа, творческая лаборатория |
|
|
Правильные многогранники |
7 |
Рассказ учителя, беседа, творческая лаборатория, геометрический бой геометрический практикум |
|
|
Тела вращения |
2 |
Творческая лаборатория |
|
|
Золотое сечение |
5 |
Проект |
|
|
Многогранники в искусстве и архитектуре |
4 |
Рассказ учителя, беседа, творческая лаборатория, проект |
|
|
Моделирование многогранников |
8 |
Творческая лаборатория, геометрический бой |
|
Всего |
68 |
||
Содержание программы
5 класс
Тема 1. Модуль «Плоскостное моделирование» — 35 ч
Первые шаги в геометрии — 13 ч
Простейшие геометрические фигуры: прямая, луч, отрезок, многоугольник. Углы, их построение и измерение. Транспортир. Биссектриса угла. Вертикальные и смежные углы. Треугольники. Виды треугольников. Построение треугольников. Сумма углов треугольника. Неравенство треугольника. Периметр. Многоугольники. Вывод формулы для вычисления суммы углов правильных выпуклых многоугольников. Квадрат. Графическая работа «Знает даже и дошкольник, что такое треугольник»
Фигуры на плоскости — 8 ч
Задачи со спичками. Задачи на разрезание и складывание фигур: «Сложи квадрат», «Согни и отрежь», «Край в край». Танграм. Стомахион. Пентамино. Гексамино. Проект «Математические головоломки»(см. КИМы).
Площади многоугольников — 10 ч
Площадь прямоугольника. Площадь квадрата. Площадь треугольника. Понятия: высота, медиана, биссектриса треугольника. Масштаб. Построение геометрических фигур в масштабе. Решение задач практического характера. Урок-проект «Классный ремонт!». Сравнение углов наложением.
Топологические опыты — 4 ч
Фигуры одним росчерком пера. Листы Мебиуса. Граф. Проект «Паркет».
Тема 2. Модуль «Объемное моделирование»- 33 ч
Прямоугольный параллелепипед, куб — 11 ч
Многогранники, их элементы. Конструирование и исследование прямоугольного параллелепипеда, куба (работа с таблицей). Нахождение площади поверхности прямоугольного параллелепипеда, куба. Решение практических задач. Проект «Моя комната». Фигурки из кубиков и их частей. Движение кубиков. Объём куба. Объём прямоугольного параллелепипеда. Решение практических задач.
Призмы — 6 ч
Конструирование и исследование разных видов призм (работа с таблицей). Нахождение площади поверхности призмы. Конструирование разных видов призм. Нахождение объёма различных призм. Решение практических задач. Проект «Крепость».
Пирамида — 4 ч
Конструирование и исследование разных видов пирамид (работа с таблицей). Многогранные углы. Проект «Пирамиды Египта».
Метод трех проекций — 2 ч
Метод трёх проекций. Решение практических задач.
Правильные многогранники — 5 ч
Правильные многогранники. Исследование октаэдра (работа с таблицей). Исследование икосаэдра и додекаэдра (работа с таблицей). Экскурсия по городу «Многогранники». Решение практических задач.
Организация и проведение конструкторских проектов — 5 ч
Экскурсия по городу. Проект «Мой город. Изучаем правила дорожного движения» Проект «Мой загородный дом».
6 класс
Тема 1. Модуль «Плоскостное моделирование» — 40 ч
Неравенство треугольника — 2 ч
Неравенство треугольника.Решение практических задач.
Поворот, симметрия — 14 ч
Симметрия (центральная, осевая). Поворот. Переносная (трансляционная) симметрия. Плоская решетка. Скользящая плоскость (ось) симметрии. Паркеты на плоскости. Правильные паркеты. Бордюры. Проект «Бордюры». Симметрия в архитектуре. Проект «Мой город».
Параллельность и перпендикулярность прямых — 3 ч
Параллельность прямых.Перпендикулярность прямых. Решение практических задач.
Координаты на плоскости — 7 ч
Что такое координаты? Прямоугольная система координат на плоскости. Начало координат. Координатные прямые: оси абсцисс и ординат. Координаты точки. Метод координат. Игра «Морской бой». Проект «Рисуем в координатах».
Графы. Кривые — 5 ч
Графы. Вершины и рёбра графов. Уникурсальные графы. Задача Эйлера о кёнигсбергских мостах. Задачи о раскрашивании карт.
Окружность. Геометрические места точек — 9 ч
Окружность и круг. Центр и радиус окружности. Хорда и диаметр окружности. Взаимное расположение двух окружностей. Число π. Длина окружности. Геометрическое место точек. Почему люки круглые? Окружности и круг в архитектуре. Шар, сфера и их элементы.
Тема 2, Модуль «Объемное моделирование» — 28 ч
Пирамида — 4 ч
Кристаллы — природные многогранники. Пирамида, усеченная пирамида.Объём пирамиды. Расчёт по формуле. Решение практических задач на вычисление объёма.
Правильные многогранники — 7 ч
Пифагорейская школа. Правильные многогранники. Теорема Эйлера. Эйлеровы многогранники. Многогранники с дырами. Многогранные углы. Типы правильных многогранников.
Тела вращения — 2 ч
Цилиндр, конус. Развертка и построение моделей
«Золотое сечение» — 5 ч
Тайны «Золотого сечения». «Золотое сечение»в архитектуре, скульптуре, живописи, человеке, природе. Пентакль. Проект «Золотое сечение»
Многогранники в искусстве и архитектуре — 4 ч
Звездчатые многогранники. Тела Архимеда. Проект «Многогранники в архитектуре города».
Моделирование многогранников — 8 ч
Правильные многогранники. Развертка. Куб, развертка куба. Правильный тетраэдр, развертка тетраэдра. Правильный октаэдр, развертка октаэдра. Правильный икосаэдр, развертка икосаэдра. Правильный додекаэдр, развертка додекаэдра. Заполнение пространства правильными многогранниками. Симметрия многогранников.
Контрольно-измерительные материалы
- Геометрический практикум (решение нестандартных задач)
- Геометрический бой (решение разноуровневых олимпиадных задач в формате командного математического боя). Матбой — это соревнование двух команд в решении х задач, подобранных жюри, в умении представлять решения у доски и в умении проверять чужие решения. Команды получают одинаковые задачи, и решают их в разных помещениях заданное время, потом собираются вместе для проверки решений. Таким образом, матбой состоит из двух частей: решения задач и собственно боя.
- Графическая работа (выполнение чертежа, рисунка на чертёжном формате А4)
- Творческая лаборатория (мини-исследование)
- 3D-моделирование многогранников, изготовление поделок в технике оригами
- Тестирование
- Информационные, исследовательские, практико-значимые проекты
- Задание по теме «Первые шаги вгеометрии»
Назови геометрические фигуры, из которых составлены человечки. Определи, сколько треугольников, окружностей, четырехугольников, овалов в каждом изображении
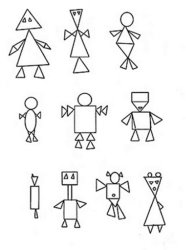
Рис. 1. Иллюстрация к заданию
- Творческое лаборатория по теме «Фигуры на плоскости»— «Танграм»
С помощью чертежа изготовь фигуры танграма. Сложи из них изображения на картинке.
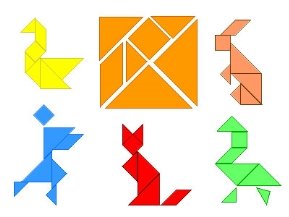
Рис. 2. Танграм
- Проектно-исследовательская работа по теме «Фигуры на плоскости»— «Математические головоломки. Полимино» (фрагмент)
Вроде простою казалась задача -
Всё же от вас отвернулась удача.
Вам теперь плакать хочется громко?
Значит — это головоломка!
Матвеева Т.
Проект посвящен полимино — одной из самых известных и занимательных математических головоломок.
Цель проекта- исследование всех возможных видов и комбинаций полимино.
Задачи, стоящие перед проектной группой:
– Узнать, кто изобрёл полимино
– Найти и подсчитать количество всех возможных фигур для каждого вида головоломки
– Научиться составлять различные фигуры из полимино
– Рассказать об этой интереснейшей головоломке одноклассникам
Полимино, или полиомино (англ. polyomino) — плоские геометрические фигуры, образованные путём соединения нескольких одноклеточных квадратов по их сторонам.
Полимино существует много видов: мономино (1 квадрат), домино (2 квадрата), тримино (3 квадрата), тетрамино (4 квадрата), пентамино (5 квадратов), гексамино(6 квадратов), гептамино (7 квадратов) и т. д..
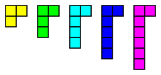
Рис. 3. Виды полимино
Существует только один тип домино, два типа тримино и пять типов тетрамино.
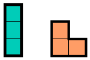
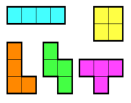
Рис. 4. Тримино и тетрамино
На кружке мы смогли определить, что у пентамино число различных фигур 12.
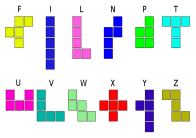
Рис. 5. Пентамино
На занятии, а потом и дома выяснили, что существует 35 различных разновидностей гексамино, а потом на сайте, посвященном полимино, узнали, что есть 108 разновидностей гептамино.

Рис. 6. Гексамино
Число различных полимино данного порядка, зависит от того, из скольких квадратов составлены фигуры (то есть от порядка), но пока еще никому не удалось найти формулу, выражающую эту связь.
Литература:
- Шарыгин И. Ф., Ерганжиева Л. Н. Наглядная геометрия. Учебное пособие для 5–6 класс. М.: Дрофа, 2000 г.
- Т. Г. Ходот, А. Ю. Ходот. Учебник для учащихся 5,6 кл. «Наглядная геометрия» М.: Просвещение, 2014.
- Смирнов В. И.. Учебник для учащихся 5,6 кл. «Наглядная геометрия» М.: МЦНМО, 2015.
- Головин Д. А., Дубровский Е. Э., Ловков К. И., Шамшурина Ю. С., Ястребов М. И., Шмелева О. В. Математические головоломки: полимино // Юный ученый. — 2016. — № 6.1. — С. 21–23.
- https://infourok.ru/rabochaya-programma-po-kursu-naglyadnaya-geometriya-klassi-393982.html
- http://nsportal.ru/shkola/geometriya/library/2014/01/08/rabochaya-programma-vneurochnoy-deyatelnosti-naglyadnaya
Похожие статьи
Математический кружок «Наглядная геометрия» для учащихся...
Простейшие геометрические фигуры. 1. 3 неделя.
12 неделя. 13. Многогранники. Параллелепипед и его свойства. 1. 13 неделя.
Решение занимательных геометрических задач.
Развитие творческого мышления учащихся при изучении понятий...
Например, это можно объяснить в примере куба со следующей логической цепочкой: куб — прямоугольный параллелепипед — призма — многогранник — геометрическое тело – множество точек пространства.
Математическая мозаика | Статья в журнале «Школьная педагогика»
Решение олимпиадных задач. Геометрическая мозаика. 21. Геометрия на клетчатой бумаге.
Развертка прямоугольного параллелепипеда.
Темы исследовательских работ. Одной из самых сложных задач в проектах является выбор темы исследовательской работы учащихся...
О геометрических преобразованиях и его приложениях...
Типы правильных многогранников. К вопросу построения различных геометрических фигур на одной...
При осуществлении классификации учащиеся должны выделять следующие виды многогранников: параллелепипед, прямоугольный параллелепипед, куб, призма...
GeoGebra как средство решения стереометрических задач
Все соответствующие многогранники можно построить, взяв за основу куб. Саранцев Г. И. Сборник задач на геометрические преобразования.Издание: второе, переработанное и... Развитие творческого мышления учащихся при изучении понятий...
Математическое моделирование в детском саду
пространственное моделирование на базе разрезания прямоугольного параллелепипеда
Из нескольких частей, представляющих собой простейшие геометрические фигуры, сложить определённую форму
Моделирование на базе оригами – творческий процесс для педагога.
GeoGebra как средство визуализации решения задач на уроках...
Использование информационных технологий на уроках позволяет учителю грамотно решать сразу несколько задач
Реализовать принцип наглядности, сделать математические факты зримыми и более понятными учителю помогут «интерактивные геометрические среды» (ИГС).
Развитие пространственных представлений учащихся при...
Школьные учителя математики, ученые-методисты предполагают две основные причины такого положения
2. Лабораторные работы. Исследование свойств геометрических фигур. Изготовление моделей многогранников [3, с. 205–206].
Особенности организации школьных геометрических олимпиад
Рассмотрим особенности организации геометрических олимпиад в мировой практике.
Параллелепипеды. Многогранники.
Геометрический бой (решение разноуровневых олимпиадных задач в формате командного математического боя).
Похожие статьи
Математический кружок «Наглядная геометрия» для учащихся...
Простейшие геометрические фигуры. 1. 3 неделя.
12 неделя. 13. Многогранники. Параллелепипед и его свойства. 1. 13 неделя.
Решение занимательных геометрических задач.
Развитие творческого мышления учащихся при изучении понятий...
Например, это можно объяснить в примере куба со следующей логической цепочкой: куб — прямоугольный параллелепипед — призма — многогранник — геометрическое тело – множество точек пространства.
Математическая мозаика | Статья в журнале «Школьная педагогика»
Решение олимпиадных задач. Геометрическая мозаика. 21. Геометрия на клетчатой бумаге.
Развертка прямоугольного параллелепипеда.
Темы исследовательских работ. Одной из самых сложных задач в проектах является выбор темы исследовательской работы учащихся...
О геометрических преобразованиях и его приложениях...
Типы правильных многогранников. К вопросу построения различных геометрических фигур на одной...
При осуществлении классификации учащиеся должны выделять следующие виды многогранников: параллелепипед, прямоугольный параллелепипед, куб, призма...
GeoGebra как средство решения стереометрических задач
Все соответствующие многогранники можно построить, взяв за основу куб. Саранцев Г. И. Сборник задач на геометрические преобразования.Издание: второе, переработанное и... Развитие творческого мышления учащихся при изучении понятий...
Математическое моделирование в детском саду
пространственное моделирование на базе разрезания прямоугольного параллелепипеда
Из нескольких частей, представляющих собой простейшие геометрические фигуры, сложить определённую форму
Моделирование на базе оригами – творческий процесс для педагога.
GeoGebra как средство визуализации решения задач на уроках...
Использование информационных технологий на уроках позволяет учителю грамотно решать сразу несколько задач
Реализовать принцип наглядности, сделать математические факты зримыми и более понятными учителю помогут «интерактивные геометрические среды» (ИГС).
Развитие пространственных представлений учащихся при...
Школьные учителя математики, ученые-методисты предполагают две основные причины такого положения
2. Лабораторные работы. Исследование свойств геометрических фигур. Изготовление моделей многогранников [3, с. 205–206].
Особенности организации школьных геометрических олимпиад
Рассмотрим особенности организации геометрических олимпиад в мировой практике.
Параллелепипеды. Многогранники.
Геометрический бой (решение разноуровневых олимпиадных задач в формате командного математического боя).







