Параметрический синтез системы управления двухдвигательного вентильного электропривода на ЭВМ
Автор: Самсоненко Анатолий Иванович
Рубрика: 5. Энергетика
Опубликовано в
III международная научная конференция «Технические науки: теория и практика» (Чита, апрель 2016)
Дата публикации: 31.03.2016
Статья просмотрена: 172 раза
Библиографическое описание:
Самсоненко, А. И. Параметрический синтез системы управления двухдвигательного вентильного электропривода на ЭВМ / А. И. Самсоненко. — Текст : непосредственный // Технические науки: теория и практика : материалы III Междунар. науч. конф. (г. Чита, апрель 2016 г.). — Чита : Издательство Молодой ученый, 2016. — С. 80-85. — URL: https://moluch.ru/conf/tech/archive/165/9977/ (дата обращения: 27.04.2024).
В данной статье рассматриваются схема двухдвигательного вентильного электропривода, приведен алгоритм параметрического синтеза системы управления электроприводом.
Ключевые слова: двухдвигательный вентильный электропривод, нелинейное корректирующее устройство, качество переходных процессов, алгоритм параметрического синтеза системы, метод Ляпунова, функции многих переменных, численный метод сканирования.
This article discusses thescheme ofthe twin-enginevalveelectric drive. Also,the algorithm ofparametric synthesis ofelectric drive control system was developed.
Keywords: twin-engine valve electric drive, the non-linear correcting device, quality of transient processes, algorithm of parametric synthesis of system, Functions of many variables, Lyapunov's method, the scanning numerical method.
Структурная схема замкнутого двухдвигательного вентильного электропривода с нелинейным корректирующим устройством [1] в системе MATLAB представлена на рисунке 1.
Структурная схема двухдвигательного вентильного электропривода (ДВЭП) состоит из двух идентичных структурных схем вентильных двигателей [2], преобразователя частоты [3] и нелинейного корректирующего устройства аналогичного звену переменной структуры.
Нелинейное корректирующее устройство в известной мере дает возможность ослабить влияние возмущающих воздействий на систему управления и повысить качество переходных процессов скоростей двигателей ДВЭП.
Так как параметры вентильного двигателя заданы, то определению подлежат постоянные времени нелинейного корректирующего устройства (НКУ) и коэффициента передачи преобразователя частоты.
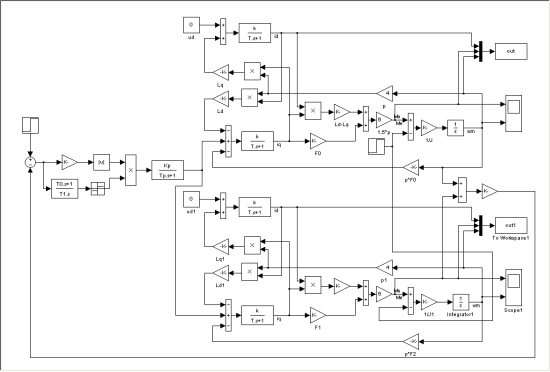
Рис. 1. Структурная схема двухдвигательного вентильного электропривода
Нелинейное корректирующее устройство показано на рисунке 2.
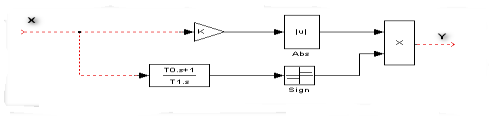
Рис. 2. Схема нелинейного корректирующего устройства
Коэффициент передачи преобразователя частоты и постоянные времени НКУ должны определяться таким образом, чтобы удовлетворялись условия устойчивости и динамические характеристики переходного процесса двухдвигательного вентильного электропривода. Структурная схема алгоритма [4] параметрического синтеза системы управления [4] ДВЭП приведена на рисунке 3.
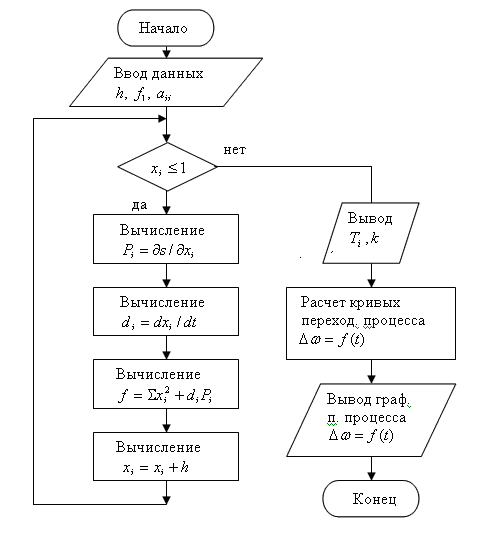
Рис. 3. Структурная схема алгоритма синтеза системы
Следует отметить, что алгоритм параметрического синтеза системы управления ДВЭП основан на использовании второго метода Ляпунова [5], численного метода сканирования [6], с использованием случайных чисел для задания параметров синтеза системы, и математического описания динамики замкнутого ДВЭП.
Дифференциальные уравнения динамики движения замкнутого двухдвигательного вентильного электропривода имеют вид:
![]() (1)
(1)
![]() (2)
(2)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
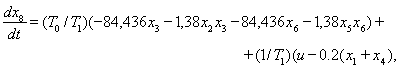 (8)
(8)
где ![]() - — угловые скорости вращения вала двигателей,
- — угловые скорости вращения вала двигателей, ![]() — проекции тока статора.
— проекции тока статора.
Постоянные времени НКУ и коэффициент передачи преобразователя частоты в уравнениях (1–8) обозначены: ![]()
Алгоритм расчета параметров НКУ и коэффициента передачи преобразователя частоты заключается в следующем:
Вводятся исходные данные, шаг сканирования по каждой переменной, начальное значение функции переменных, а также коэффициенты ![]() , как случайные числа, функции s квадратичной формы;
, как случайные числа, функции s квадратичной формы;
Вычисляются частные производные функции s квадратичной формы;
Вычисляются правые части дифференциальных уравнений (1–8);
Вычисляются минимальные значения функции многих переменных ![]() .
.
В логическом операторе ![]() проверяется условие окончания счета. В случае его выполнения осуществляется переход к дальнейшему этапу синтеза искомых параметров. Если условие не выполняется, то осуществляется процесс вывода результата счета, т. е. осуществляется вывод численных значений определяемых параметров
проверяется условие окончания счета. В случае его выполнения осуществляется переход к дальнейшему этапу синтеза искомых параметров. Если условие не выполняется, то осуществляется процесс вывода результата счета, т. е. осуществляется вывод численных значений определяемых параметров ![]() и кривые переходного процесса скоростей двигателей двухдвигательного вентильного электропривода.
и кривые переходного процесса скоростей двигателей двухдвигательного вентильного электропривода.
Программа синтеза параметров системы управления:
function PROG1
globalkp; global T0; global T1;
n=8; r=0; m=10;
fori=1:m
h=0.5; q1=1.0e6;
kp=rand*100; T0=rand*0.5; T1=rand;
x(8)=0.1; while x(8)<=1 x(7)=0.1; while x(7)<=1
x(6)=0.1; while x(6)<=1 x(5)=0.1; while x(5)<=1
x(4)=0.1; while x(4)<=1 x(3)=0.1; while x(3)<=1
x(2)=0.1; while x(2)<=1 x(1)=0.1; while x(1)<=1
h1=0.01;
i=1; whilei<=n
u(i)=x(i)+h;
v(i)=x(i)-h;
j=1;while j<=n
if j~=i u(j)=x(j);v(j)=x(j);end;
j=j+1;
end
z1=u(1); z2=u(2); z3=u(3); z4=u(4);
z5=u(5); z6=u(6); z7=u(7); z8=u(8);
f2=kvfun119(z1,z2,z3,z4,z5,z6,z7,z8);
z1=v(1); z2=v(2); z3=v(3); z4=v(4);
z5=v(5); z6=v(6); z7=v(7); z8=v(8);
f3=kvfun119(z1,z2,z3,z4,z5,z6,z7,z8);
a(i)=((f2-f3)/2)/h;
i=i+1;
end
d(1)=84.436*x(3)+1.38*x(2)*x(3); d(2)=1.71*x(1)*x(3)-181.8*x(2);
d(3)=444.4*x(8)-9.3*x(1)*x(2)-325.3*x(1)-427.3*x(3);
d(4)=84.436*x(6)+1.38*x(5)*x(6); d(5)=1.71*x(4)*x(6)-181.8*x(5);
d(6)=444.4*x(8)-9.3*x(4)*x(5)-325.3*x(4)-427.3*x(6);
d(7)=1000*kp*abs(-0.9*(x(1)+x(4)))*sign(x(8))-1000*x(7);
d(8)=(T0/T1)*(-84.436*x(3)-1.38*x(2)*x(3)-...
84.43*x(6)-1.38*x(5)*x(6))+(1/T1)*(-0.9*(x(1)+x(4)));
q=abs(x(1)^2+x(2)^2+x(3)^2+x(4)^2+x(5)^2+x(6)^2+x(7)^2+ x(8)^2+...
d(1)*a(1)+d(2)*a(2)+d(3)*a(3)+d(4)*a(4)+d(5)*a(5)+...
d(6)*a(6)+d(7)*a(7)+d(8)*a(8));
if q<=q1 q1=q; y(1)=x(1);y(2)=x(2);y(3)=x(3);...
y(4)=x(4);y(5)=x(5);y(6)=x(6);y(7)=x(7);...
y(8)=x(8);end
x(1)=x(1)+h;end; x(2)=x(2)+h;end
x(3)=x(3)+h;end; x(4)=x(4)+h;end
x(5)=x(5)+h;end; x(6)=x(6)+h;end
x(7)=x(7)+h;end; x(8)=x(8)+h;end
r=r+1;
if r>=m break;end;
end
clc
disp('kp=');disp(kp); disp('T0=');disp(T0); disp('T1=');disp(T1);
y0 = [0;0;0;0;0;0;0;0];
[T,Y]=ode113(@sysdk,[0 10],y0);
plot(T,Y(:,1),'k.-',T,Y(:,4),'b.-');
xlabel('\itt')
legend('scorost', 4)
gridon
holdoff
function F = sysdk(t,y)
u=10;
F = [84.43*y(3)+1.38*y(2)*y(3);1.7*y(1)*y(3)-181.8*y(2);...
444.4*y(8)-9.3*y(1)*y(2)-325.3*y(1)-427.3*y(3);...
84.43*y(6)+1.38*y(5)*y(6);1.71*y(4)*y(6)-181.8*y(5);...
444.4*y(8)-9.3*y(4)*y(5)-325.3*y(4)-427.3*y(6);...
1000*kp*abs(u-0.9*(y(1)+y(4)))*sign(y(8))-1000*y(7);
(T0/T1)*(-84.436*y(3)-1.38*y(2)*y(3)-...
84.43*y(6)-1.38*y(5)*y(6))+(1/T1)*(u-0.9*(y(1)+y(4)))];
end
end
Рисунок 4.
Подпрограмма kvfun119.
function f=kvfun119(z1,z2,z3,z4,z5,z6,z7,z8)
n=8; k=1;
while k<=n
l=k;
while l<=n
b(k,l)=1;
l=l+1;
end
k=k+1;
end
f=b(1,1)*z1^2+b(1,2)*z1*z2+b(1,3)*z1*z3+b(1,4)*z1*z4+...
b(1,5)*z1*z5+b(1,6)*z1*z6+b(1,7)*z1*z7+b(1,8)*z1*z8+...
b(2,2)*z2^2+b(2,3)*z2*z3+b(2,4)*z2*z4+b(2,5)*z2*z5+...
b(2,6)*z2*z6+b(2,7)*z2*z7+b(2,8)*z2*z8+b(3,3)*z3^2+...
b(3,4)*z3*z4+b(3,5)*z3*z5+b(3,6)*z3*z6+b(3,7)*z3*z7+...
b(3,8)*z3*z8+b(4,4)*z4^2+b(4,5)*z4*z5+b(4,6)*z4*z6+...
b(4,7)*z4*z7+b(4,8)*z4*z8+b(5,5)*z5^2+b(5,6)*z5*z6+...
b(5,7)*z5*z7+b(5,8)*z5*z8+b(6,6)*z6^2+b(6,7)*z6*z7+...
b(6,8)*z6*z8+b(7,7)*z7^2+b(7,8)*z7*z8+b(8,8)*z8^2;
График скоростей ДВЭП получается с наложением один на другой, т. е. по форме и по численным значением одинаковые. График скоростей показан на рисунке 4.
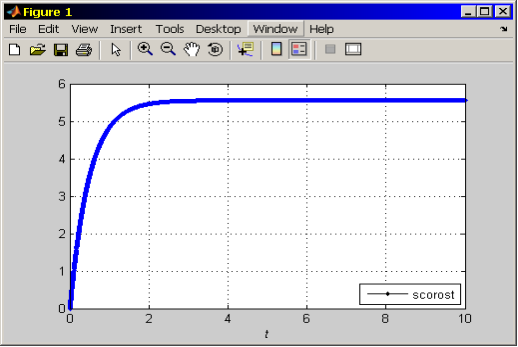
Рис. 4. График угловой скорости вентильного двигателя
Полученный график угловых скоростей каждого вентильного двигателя (кривые переходного процесса скоростей совпадают) является одним из вариантов счета программы синтеза параметров системы управления ДВЭП.
Результаты вычислений определяемых параметров системы получаются следующими: kp=49.4, Т0= 0.31, T1= 0.4.
Вывод. Применение нелинейного корректирующего устройства для ослабления влияния возмущающих воздействий на систему управления дает положительный результат при моделировании в системе MATLAB и повышает качество переходных процессов скоростей двигателей ДВЭП. Численный метод сканирования, с использованием случайных чисел для задания параметров синтеза системы упрощает решение дифференциальных уравнений с многими переменными и позволяет оперативно выводить графики переходного процесса скоростей двигателей двухдвигательного вентильного электропривода.
Литература:
- Попов Е. П. Теория нелинейных систем автоматического регулирования и управления. — М.: Наука, 1988, с. 202–204.
- Герман-Галкин С. Г. Matlab & Simulink. Проектирование мехатронных систем на ПК. — СПб.: Корона — Век, 2008, с. 330–331.
- Терехов В. М., Осипов О. И. Системы управления электроприводов. — М.: Издательский центр «Академия», 2008, с. 197–198.
- Сагитов П. И., Тергемес К. Т., Шадхин Ю. И. Параметрический синтез системы управления многодвигательного асинхронного электропривода // Вестник Алматинского университета энергетики и связи. — 2011, № 2 (13), с. 63–66.
- Фельдбаум А. А., Бутковский А. Г. Методы теории автоматического управления. — М.: Наука, 1971, с. 312–322.
- Бояринов А. И., Кафаров В. В. Методы оптимизации в химической технологии. — М.: 1975, с. 508–512.
Ключевые слова
двухдвигательный вентильный электропривод, нелинейное корректирующее устройство, качество переходных процессов, алгоритм параметрического синтеза системы, метод Ляпунова, функции многих переменных, численный метод сканирования., численный метод сканированияПохожие статьи
Метод структурного и параметрического синтеза и анализа...
Параметрический синтез системы управления двухдвигательного вентильного электропривода на ЭВМ.
Исследования нелинейного корректирующего устройства... Структурная схема алгоритма параметрического синтеза нелинейной системы...
Исследования нелинейного корректирующего устройства...
Структурная схема алгоритма параметрического синтеза нелинейной системы управления приведена на рисунке 2. Структурная схема алгоритма построена на основании [3].
Анализ устойчивости замкнутой нелинейной системы...
переходных процессов системы автоматического управления и по фазовым траекториям определять устойчивость системы управления. Структурная схема замкнутой системы ПЧ-АД с нелинейным статическим звеном в MATLAB представлено на рисунке 1.
Анализ передаточной функции структурной схемы вентильного...
Структурная схема вентильного двигателя в системе MATLAB представлена на рисунке 1. В линеаризованной структурной схеме вентильного двигателя является угловой скорость частоты вращения вала двигателя.
Исследование параметров управляющего устройства...
Ключевые слова: асинхронный электропривод, преобразователь частоты, среда MATLAB, управляющее устройство, энергосберегающий электропривод, система управления.
Алгоритм синтеза прогнозирующего управления...
Структурная схема вентильного двигателя в системе MATLAB представлена на рисунке 1. В линеаризованной структурной схеме вентильного двигателя является угловой скорость частоты вращения вала.
Исследование нелинейной системы «Преобразователь...»
Исследование нелинейной системы «Преобразователь частоты – асинхронный двигатель». Автор: Касымова Айнур Есбергеновна.
Структурная схема нелинейной системы ПЧ-АД в среде MATLAB представлена на рисунке 1.
Исследование методов оптимизации энергосбережения...
Ключевые слова: асинхронный электропривод, математическая модель, обратная связь, система MATLAB, переходные процессы.
Рис. 1. Структурная схема системы ПЧ-АД. На схеме приняты следующие обозначения: β — модуль жесткости механической характеристики...
Синтез регулятора системы управления электроприводами...
Исследование нелинейной системы «Преобразователь частоты...» ...звена регулятора скорости; передаточный коэффициент преобразователя частоты; коэффициент обратной связи по скорости.
Похожие статьи
Метод структурного и параметрического синтеза и анализа...
Параметрический синтез системы управления двухдвигательного вентильного электропривода на ЭВМ.
Исследования нелинейного корректирующего устройства... Структурная схема алгоритма параметрического синтеза нелинейной системы...
Исследования нелинейного корректирующего устройства...
Структурная схема алгоритма параметрического синтеза нелинейной системы управления приведена на рисунке 2. Структурная схема алгоритма построена на основании [3].
Анализ устойчивости замкнутой нелинейной системы...
переходных процессов системы автоматического управления и по фазовым траекториям определять устойчивость системы управления. Структурная схема замкнутой системы ПЧ-АД с нелинейным статическим звеном в MATLAB представлено на рисунке 1.
Анализ передаточной функции структурной схемы вентильного...
Структурная схема вентильного двигателя в системе MATLAB представлена на рисунке 1. В линеаризованной структурной схеме вентильного двигателя является угловой скорость частоты вращения вала двигателя.
Исследование параметров управляющего устройства...
Ключевые слова: асинхронный электропривод, преобразователь частоты, среда MATLAB, управляющее устройство, энергосберегающий электропривод, система управления.
Алгоритм синтеза прогнозирующего управления...
Структурная схема вентильного двигателя в системе MATLAB представлена на рисунке 1. В линеаризованной структурной схеме вентильного двигателя является угловой скорость частоты вращения вала.
Исследование нелинейной системы «Преобразователь...»
Исследование нелинейной системы «Преобразователь частоты – асинхронный двигатель». Автор: Касымова Айнур Есбергеновна.
Структурная схема нелинейной системы ПЧ-АД в среде MATLAB представлена на рисунке 1.
Исследование методов оптимизации энергосбережения...
Ключевые слова: асинхронный электропривод, математическая модель, обратная связь, система MATLAB, переходные процессы.
Рис. 1. Структурная схема системы ПЧ-АД. На схеме приняты следующие обозначения: β — модуль жесткости механической характеристики...
Синтез регулятора системы управления электроприводами...
Исследование нелинейной системы «Преобразователь частоты...» ...звена регулятора скорости; передаточный коэффициент преобразователя частоты; коэффициент обратной связи по скорости.











