Ключевые слова: регулирование, стабилизация, управление техническими системами, автоматическое управление.
Нередко в нашей жизни требуется поддерживать какое-то необходимое значение, препятствуя внешним возмущениям. Например, температуру в печи, курс корабля, устойчивость автомобиля при заносе. Но человек может справиться не со всеми задачами. Там, где важна точность или надёжность, человеческий фактор может привести к нежелательным последствиям. В таком случае на помощь приходит автоматическое управление, которое осуществляется специальным устройством — регулятором,
Цель данной статьи — подобрать регулятор для системы управления электроприводами канала наведения по горизонту платформы стабилизированной и установление оптимальных параметров корректирующих звеньев, используя среду моделирования MatlabSimulink. В данном случаем электроприводом является двигатель серии ДБМ с полезной нагрузкой в виде стойки, установленной на поворотной части погона устройства.
Управляющим воздействием будут являться два типа сигнала: синус и меандр. Синус моделирует режим слежения, а меандр переброс между режимами. При этом время отработки сигнала 1 мрад не должно превышать 0,05 с до уровня ошибки ±0,05 мрад, при этом перерегулирование должно быть не более 25 %.
Синтез регулятора.
Существуют три основных принципа автоматического управления:
– принцип разомкнутого управления,
– управление по возмущению,
– принцип обратной связи. [1]
Принцип разомкнутого управления состоит в том, что мы уверены в незначительности возмущений, и управление объектом происходит только входным воздействием.
Управление по возмущению означает, что управляющие воздействия корректируются регулятором, то есть регулятор получает информацию о возмущениях и выдает на объект такой сигнал, который подавит возмущения.
Самым эффективным при непредсказуемых возмущениях является принцип обратной связи. При таком управлении на вход поступает разность между входным сигналом и отработанным, что позволяет уменьшить ошибку регулирования.
Регуляторы бывают нескольких типов: П-, ПИ-, ПД- и ПИД-регуляторы. Подберем регулятор для управления электроприводами канала ГН платформы стабилизированной.
П-регулятор. П-регулятор представляет собой усилительное (пропорциональное) звено. Пропорциональное звено — это коэффициент пропорциональности между входным и выходным сигналами. Оно уменьшает статическую ошибку.
Исследуем П-регулятор, подставив в модель. Оптимальную величину коэффициента подберем эмпирически.
![]()
Посмотрим реакцию системы на разные входные сигналы.
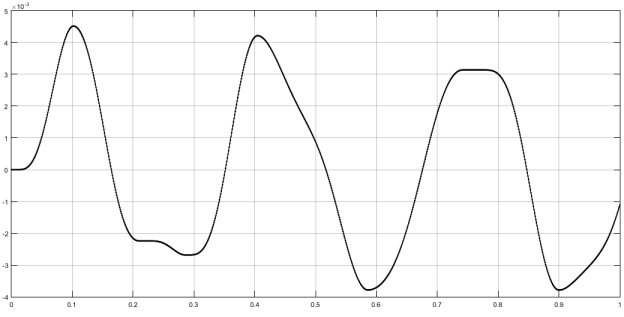
Рис. 1. Реакция системы с П-регулятором на входное синусоидальное воздействие ![]() мрад
мрад
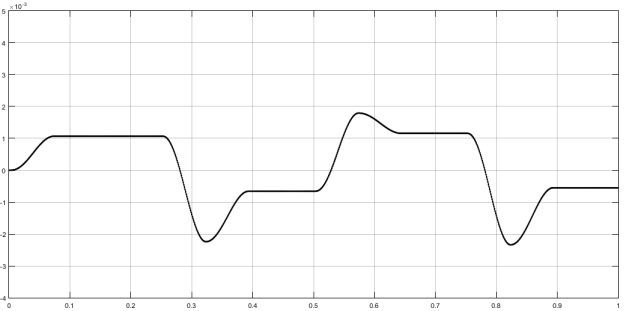
Рис. 2. Реакция системы с П-регулятором на входное воздействие вида меандр
![]()
![]()
![]()
ПИ-регулятор.
ПИ-регулятор сочетает пропорциональное и интегральное звено. Интегральное звено — это интеграл сигнала рассогласования, оно накапливает значение невязки и поддерживает заданное значение регулируемой величины. Передаточная функция интегрального звена имеет вид: ![]() .
.
Исследуем ПИ-регулятор, подставив в модель. Оптимальную величину коэффициентов П- и И-звена подберем эмпирически.
![]()
Посмотрим реакцию системы на разные входные сигналы.
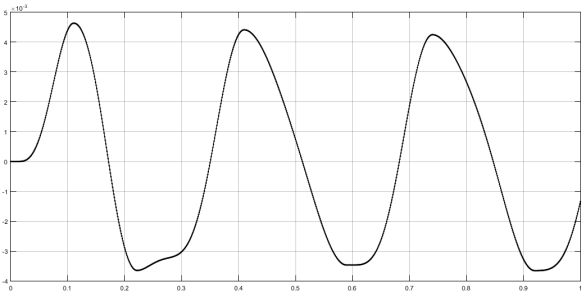
Рис. 3. Реакция системы с ПИ-регулятором на синусоидальное воздействие
![]() мрад
мрад
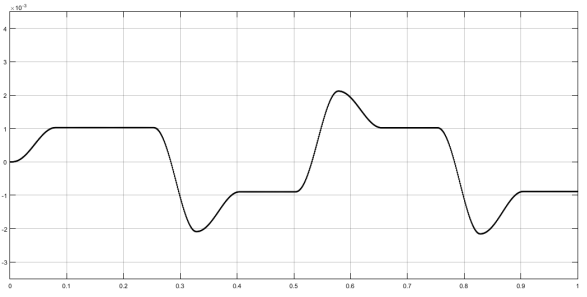
Рис. 4. Реакция системы с ПИ-регулятором на воздействие вида меандр
![]() ;мрад
;мрад
![]() .
.
Интегральная составляющая убрала колебательность, увеличилось быстродействие, но установившаяся ошибка слишком велика.
ПД-регулятор.
ПД-регулятор состоит из пропорционального и дифференциального звена. Дифференциальное звено — это дифференциал сигнала рассогласования, то есть разница между предыдущей невязкой и невязкой настоящей. Дифференцирующее звено снижает управляющее воздействие, ускоряет реакцию системы. Передаточная функция идеального дифференциального звена имеет вид: ![]() . Но идеального дифференциатора в реальной жизни не существует, поэтому он заменяется на инерционное дифференцирующее звено с передаточной функцией
. Но идеального дифференциатора в реальной жизни не существует, поэтому он заменяется на инерционное дифференцирующее звено с передаточной функцией ![]() , где T- постоянная времени, численно равная скорости реакции объекта управления. [2]
, где T- постоянная времени, численно равная скорости реакции объекта управления. [2]
Исследуем ПД-регулятор, подставив в модель. Оптимальную величину коэффициентов П- и Д-звена подберем эмпирически.
![]()
![]()
Посмотрим реакцию системы на разные входные сигналы.
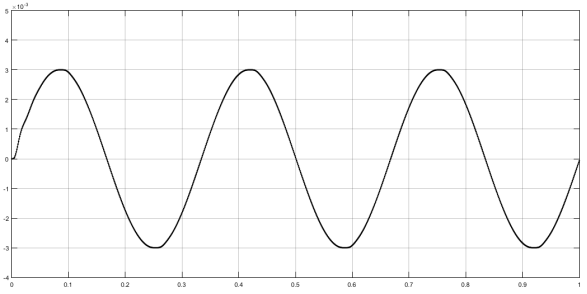
Рис. 5. Реакция системы с ПД-регулятором на синусоидальное воздействие ![]() 0.06
0.06![]() мрад
мрад
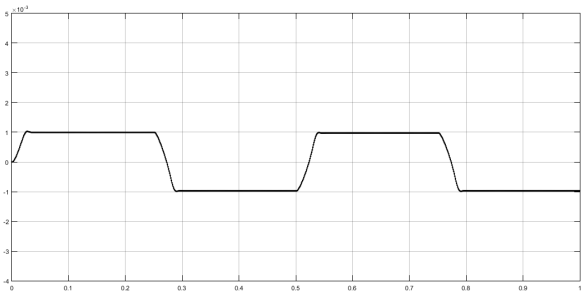
Рис. 6. Реакция системы с ПД-регулятором на воздействие вида меандр
![]() мрад
мрад
![]()
![]()
Дифференцирующая составляющая заметно улучшила время регулирования, уменьшилась установившаяся ошибка, но присутствует небольшое перерегулирование, от которого желательно избавиться.
ПИД-регулятор.
ПИД-регулятор объединяет все три звена: пропорциональное, интегральное и дифференциальное.
Коэффициенты ПИД-регулятора подберем методом Зиглера-Николса. Это классический метод предварительного подбора коэффициентов ПИД-регулятора. Метод состоит в следующем: сначала коэффициенты интегрирующей и дифференцирующей составляющих обнуляются, а пропорциональный коэффициент увеличивают до тех пор, пока в системе не начнутся автоколебание, то есть система окажется на грани неустойчивости. Это значение запоминается для последующего расчета коэффициентов регулятора, обозначим его как ![]() . Тогда
. Тогда
где Т-период автоколебаний неустойчивой системы.
Наша система без И- и Д- звеньев становится неустойчивой при ![]() , тогда запомним
, тогда запомним ![]() , при этом период автоколебаний
, при этом период автоколебаний ![]() . Рассчитаем значения коэффициентов:
. Рассчитаем значения коэффициентов:
![]()
![]()
![]()
Посмотрим реакцию системы на разные входные сигналы.
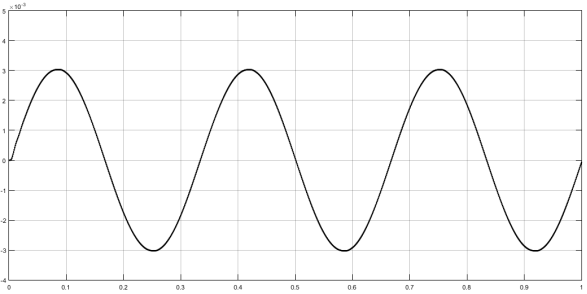
Рис. 7. Реакция системы с ПИД-регулятором на синусоидальное воздействие ![]()
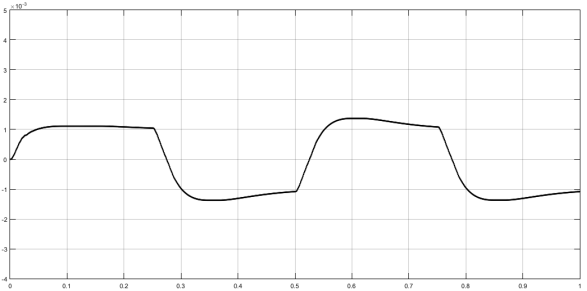
Рис. 8. Реакция системы с ПИД-регулятором на воздействие вида меандр
![]() мрад
мрад
![]()
![]() .
.
Очевидно, что величину коэффициентов необходимо скорректировать. Получим следующие значения коэффициентов:
![]()
![]()
![]()
Посмотрим реакцию системы на разные входные сигналы.
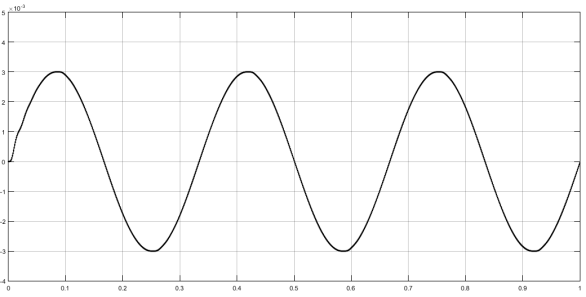
Рис. 9. Реакция системы с ПИД-регулятором на синусоидальное воздействие

Рис. 10. Реакция системы с ПИД-регулятором на воздействие вида меандр
![]()
![]()
![]() .
.
Основные критерии качества удовлетворяют требованиям тех. задания.
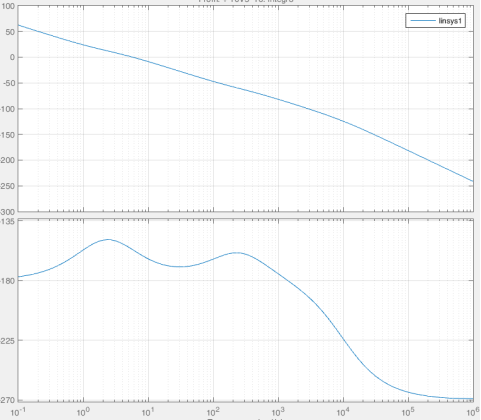
Рис. 11. АЧХ и ФЧХ системы автоматического управления электроприводами канала ГН
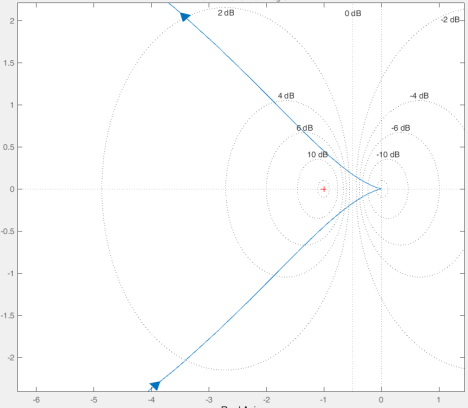
Рис. 12. Годограф системы автоматического управления электроприводами канала ГН
Из Рис.6 можно сделать вывод о том, что корни характеристического уравнения системы действительны и одного знака, а смоделированная система устойчива. [1]
Литература:
- Артамонов Д. В. Основы теории линейных систем автоматического управления — Пенз. гос. ун-та, 2003. — 142 с.
- Поляков К. Ю. Основы теории цифровых систем управления. — СПбГМТУ-СПб., 2006. — 161 с.







