Эллиптические кривые в алгоритме Диффи - Хеллмана над полем GF (2m)

Рассмотренная криптосистема Диффи-Хеллмана основана на том, что проблема логарифмирования в конечном простом поле является сложной с вычислительной точки зрения.

Ключевые слова:КриптосистемаДиффи–Хеллмана, эллиптические кривые, абелева группа, суперсингулярная кривая.

1. ВВЕДЕНИЕ

Рассмотрим протокол, криптографическая стойкость которого основана на трудности решения проблемы дискретного логарифма. Эта проблема имеет место в случае, когда задана некоторая конечная группа. Известна степень 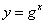 некоторого ее элемента и требуется найти значение показателя степени  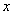— дискретный логарифм элемента 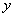. Для аддитивной группы, заданной на множестве вычетов множества  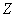целых чисел по модулю простого числа эта проблема легко решается с использованием алгоритма, подобного алгоритму Евклида. Для группы точек супер-сингулярной эллиптической кривой сложность проблемы дискретного алгоритма меньше сложности этой проблемы в общей постановке для произвольной группы. В этом случае, проблема дискретного логарифма решается эффективно.

Определение 1. [1] Пусть 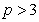 — простое число. Пусть  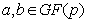такие, при которых 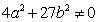. Эллиптической кривой  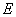над полем  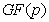называется множество решений  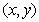уравнения:

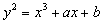                                                                                                              (1)

Над полем 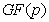 вместе с дополнительной точкой 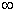, называемой точкой в бесконечности или нулевой точкой .

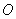Представление эллиптической кривой в виде уравнения 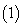 носит название эллиптической кривой в форме Вейерштрасса.

Обозначим количество точек на эллиптической кривой 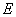 через 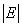. Теорема Хассе гласит, что [2]

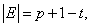
где 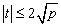,  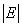называется порядком кривой 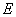, а 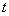 — следом кривой .

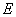Введем бинарную операцию на 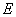 (в аддитивной записи) следующими правилами [3]:

;

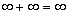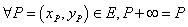
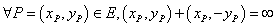                                                                  (2)

,

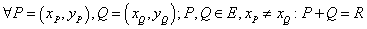где

,

,

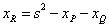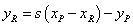и

.

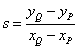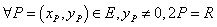, где

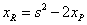,                                                                                                                (3)

,

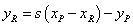и

.

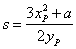Множество точек эллиптической кривой 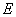 с заданной таким образом операцией образует абелеву группу.

Если 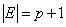, то кривая  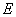называется супер-сингулярной.

Эллиптическая не являющаяся супер-сингулярной кривая 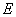 над полем 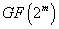, характеристики 2 задается следующим образом.

Определение 2. [1] Пусть 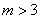 — целое число; , 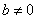. Эллиптической кривой  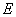над полем  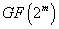называется множество решений  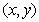уравнения:

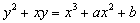                                                                                                    (4)

Над полем 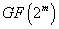 вместе с дополнительной точкой 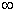, называемой точкой в бесконечности.

Количество точек на кривой 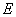 также определяется теоремой Хассе [2]:

,

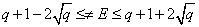где 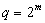. Более того,  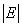четно.

Операция сложения на 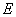 в этом случае задается следующими правилами:

;

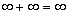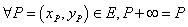
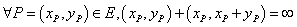                                                             (5)

,

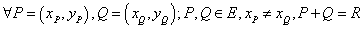где

,

,

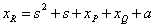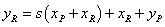и

,

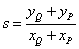
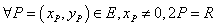где

,

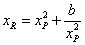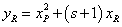
и

.

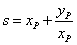В этом случае множество точек эллиптической кривой 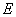с заданной таким образом операцией также образует абелевую группу.

Пользуясь операцией сложения точек на кривой, можно естественным образом определить операцию умножения точки 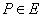 на произвольное целое число :

,

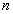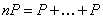где операция сложения выполняется 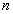 раз.

2. АЛГОРИТМЫ ВЫЧИСЛЕНИЯ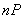

Алгоритм 1. [2]

Рассмотрим алгоритм вычисления координат точки 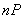, где 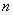 — целое число 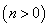,  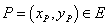— заданная точка плоскости .

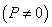Пусть 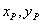 — многочлены из поля .

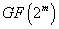Разложим число 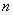 в двоичной системе:

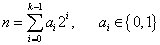,                                                                                              (6)

где .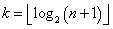

Пусть 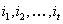  — индексы единичных компонент в наборе 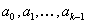. Тогда

                                                                                                            (7)

Найдем последовательность 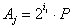,  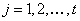по формуле:

,

,

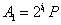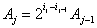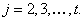
Итак, получим искомое произведение :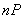

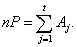
Этот алгоритм использует не более 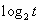 умножений многочленов на двойку и не более  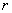операций сложения многочленов (число r — двоичное разложение n).

Алгоритм 2. Метод аддитивных цепочек [2]

Разложим 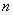 в системе счисления по основанию :

,

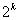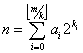по схеме Горнера [7]:

,                                                           (8)

где

.

В [2], оценка сложности 2-ого алгоритма имеет вид

,

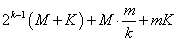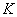где  и  — сложность сложения и удвоения точек соответственно.

Выбирая

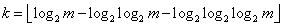
получаем асимптотически точную в общем случае оценку сложности

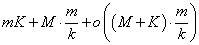.                                                                                    (9)

3. ПРИМЕНЕНИЕ ЭЛЛИПТИЧЕСКИХ КРИВЫХ В АЛГОРИТМЕ ДИФФИ-ХЕЛЛМАНА

Опишем криптографический протокол, аналогичный известному протоколу Диффи-Хэллмана. Для установления защищенной связи два пользователя А и В совместно выбирают эллиптическую кривую Е и точку Р на ней.

1 этап.

Пользователь А выбирает свое секретное целое число a (b — большое число) и вычисляет произведение 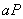. Далее А пересылает вычисленное значение получателю В.

Пользователь В генерирует свое секретное большое число b (b — целое число) и вычисляет произведение 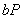. В пересылает его получателю А.

При этом параметры самой кривой, координаты точки на ней и значения произведений являются открытыми и могут передаваться по незащищенным каналам связи. Предполагается, что злоумышленник может получить оба этих значения, но не модифицировать их.

2 этап.

А на основе имеющегося у пользователя числа 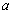и полученного по сети 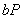вычисляет значение

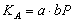
В на основе имеющегося у пользователя числа 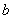и полученного по сети 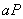вычисляет значение

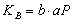
В силу свойств операции умножения на число 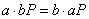, или 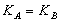. Таким образом, оба пользователя получат общее секретное значение (координаты точки ), которое они могут использовать для получения ключа шифрования.

4. СТОЙКОСТЬ АЛГОРИТМА

Отметим, что злоумышленнику для восстановления ключа потребуется решить сложную с вычислительной точки зрения задачу определения 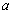 и 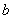 по известным  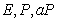и 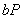. Если эта проблема имеет эффективное решение, то и проблема Диффи-Хеллмана для эллиптических также легко решаема и рассмотренный протокол не имеет смысла. В то же время гипотеза об эквивалентности проблем дискретного логарифма и проблемы Диффи-Хеллмана для эллиптических кривых не доказана.

Протокол Диффи-Хеллмана отлично противостоит пассивному нападению, но в случае реализации атаки «человек посередине» он не устоит. В самом деле, Атакующий заменяет сообщения переговоров о ключе на свои собственные и таким образом получает два ключа — свой для каждого из законных участников протокола. Далее он может перешифровывать переписку между участниками, своим ключом для каждого, и таким образом ознакомиться с их сообщениями, оставаясь незамеченным.

Литература:

1.             Алферов А. П., Зубов А. Ю., Кузьмин А. С., Черемушкин А. В. Основы криптографии. 3-е изд., испр. и доп. — М.: Гелиос АРБ. 2005.

2.             Болотов А. А., Гашков С. Б., Фролов А. Б., Часовских А. А. Алгоритмические основы эллиптической криптографии. М. Мэи. 2000.

3.             Коблиц Н. Введение в эллиптические кривые и модулярные формы. М.: Мир. 1988.

4.             Прасолов В. В., Соловьев Ю. П. Эллиптические функции и алгебраические уравнения. М.: Факториал. 1977.

5.             Степанов С. А. Арифметика алгебраических кривых. М.: Мир. 1991.

6.             Яковлев А. В., Безбогов А. А., Родин В. В., Шамкин В. Н. Криптографическая защита информации. Издательство ТГТУ. 2006.

7.             William Stallings. Cryptography and Network Security Principles and Practice. Prentice Hall. 2011.