Под длинной арифметикой понимаются выполняемые с помощью вычислительной машины арифметические операции над числами, разрядность которых превышает длину машинного слова данной вычислительной машины. Эти операции реализуются не аппаратно, а программно, с использованием базовых аппаратных средств работы с числами меньших порядков. Частный случай — арифметика произвольной точности — относится к арифметике, в которой длина чисел ограничена только объёмом доступной памяти.
Длинная арифметика применяется в различных областях компьютерных технологий. Например, в криптографии большинство систем подписывания и шифрования данных используют целочисленную арифметику по модулю m, где m — очень большое натуральное число, не обязательно простое. Например, при реализации метода шифрования RSA, криптосистемы Рабина или схемы Эль-Гамаля требуется обеспечить точность результатов умножения и возведения в степень порядка 10309. В математическое и финансовое ПО результат вычисления на бумаге должен совпадать с результатом работы компьютера с точностью до последнего разряда.
Наиболее мощные калькуляторы, реализующие длинную арифметику, имеют ряд недостатков:
- Стоимость: например, калькулятор «eCalc» стоит от 45 евро. Калькуляторы, обладающие широким функционалом и близкой к неограниченной точности вычислений, являются коммерческими продуктами;
- Ограниченный функционал: как правило, бесплатные онлайн калькуляторы имеют ряд существенных ограничений, связанных либо с точностью вычислений, либо с максимальным возможным значением. Например, один из популярных онлайн калькуляторов “web calc”, имеющий большой набор действий над числами, строить графики и вычислять значения простых функций, не находит факториалы чисел больше 200. Также данный калькулятор не дает возможности задать точность числа (устанавливается автоматически). Соответственно, если нам нужна более высокая точность, вычисления будут нести погрешность.
- Большинство бесплатных калькуляторов работают лишь с целыми числами или с ограниченной точностью.
- Закрытое ПО: большинство программ, реализующих вычисления неограниченно больших чисел с любой точностью разрабатываются для шифрования и кодирования и не находятся в открытом доступе.
Разработанный программный продукт устраняет большинство недостатков доступных аналогов:
– Работа с числами практически неограниченной длины. В отличие от большинства аналогов, программа способна манипулировать десятичными числами до 1010^9;
– Реализация всех базовых арифметических действий над числами, в том числе и деления с остатком необходимой точности;
– Возможность работы с дробными числами.
– Данный продукт способен преобразовать выражение произвольной длины, имеющее до 27 переменных (переменные в выражении могут повторяться). Операции, которые могут быть использованы в выражении:
– Повышение приоритета выполнения операций. Таким образом, арифметические действия могут производиться не только между переменными, но и между выражениями;
– сложение/вычитание чисел или выражений;
– Умножение двух чисел с заданной конечной точностью;
– Деление двух чисел. Может быть произведено с заданной точностью, а так же выделение целой части или остатка от деления;
– Возведение в степень, причем показатель степени также может быть длинным числом;
– Факториал числа или выражения;
Операции возведения в степень и факториала имеют свои ограничения, так как в данной версии продукта результат не может превышать 1010^9.Например, наибольшее число, факториал которого может быть найден — 6000. Среди бесплатных аналогов вычисление факториала такой величины обнаружено не было.
Также программа сохраняет результат в текстовый документ для дальнейшего использования и, наоборот, позволяет считать выражение и значение переменных из файла;
Хранение числа впамяти
Из различных способов представления длинных чисел в памяти компьютера для разработки программного продукта был выбран и доработан принцип поразрядного хранения, так как такие методы, как метод факторизации или разложения на простые модули ограничивают функционал программы (нет возможности работать с дробными числами, производить деление чисел).
Так как метод поразрядного хранения может привести к повышенному расходу памяти, а также к ограничению длины числа, было принято решение хранить десятичное число в системе счисления с основанием 10000 (Рис. 1):
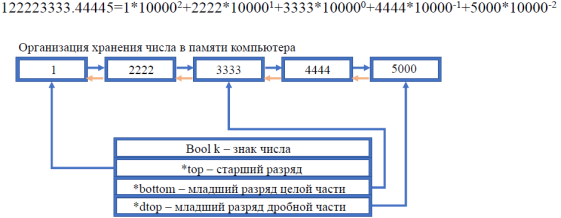
Рис. 1. Принципиальная схема хранения длинного числа
Хранение числа реализовано в двусвязном списке, к ссылкам на начало и конец числа была добавлена ссылка на младший разряд целой части. Благодаря этому ест возможность задать любую точность для хранимого числа. Число 10000 было выбрано за размер одной ячейки во избежание перегрузки элемента списка при выполнении промежуточных расчетов. Во время вычисления выражения максимальное промежуточное значение должно помещаться в переменную типа int. Максимальное промежуточное значение для числа 9999 будет 9999*9999, что помещается в переменную типа int.
Сложение ивычитание
Данные операции следует рассматривать в связке, так как суть их одинакова, а сами операции сложения и вычитания сводится к сложению или вычитанию модулей.
Стоит отметить, что для ускорения вычислений при вычитании строка выражения преобразуется следующим образом: если производится вычитание, то все последующие знаки сложения и вычитания (равного приоритета) инвертируются. Например, при вводе выражения a-b*(c+a)-a+d программа при выполнении первого вычитания фактически изменит выражение и приведет его к виду a-(b*(c+a)-a+d).
И сложение, и вычитание, выполняется после приведения в соответствие дробной части обоих чисел путем добавления нулевых разрядов в дробную часть числа, у которого она короче. После этого выполняется поразрядное сложение с проверкой переполнения разрядов (Рис. 2).
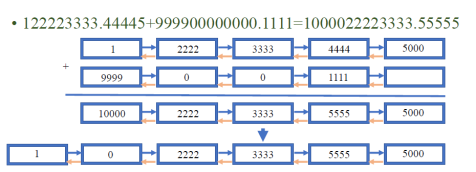
Рис. 2. Реализация операции сложения
Умножение
Умножение чисел путем последовательного сложения, с учетом длины чисел, может занять значительное количество времени. В связи с этим был реализован алгоритм поразрядного умножения, который заключается в следующем:
Умножить первый множитель на младший разряд второго с проверкой переполнения ячеек;
Повторить операция со следующим по старшинству разрядом, добавляя полученное число к результату также со сдвигом в один разряд.
Отделить дробную часть путем перемещения нужной ссылки (Рис. 3).
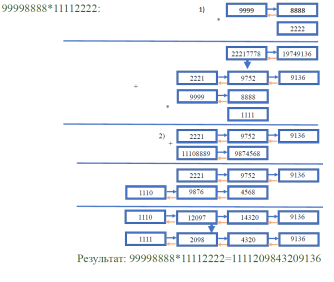
Рис. 3. Реализация операции умножения
Деление
Деление чисел путем последовательного вычитания также может занять продолжительное время (например, деление очень большого числа на очень малое). Для увеличения скорости расчетов был реализован алгоритм поразрядного деления. Алгоритм сводится к выполнению следующих действий:
- Ссылки на младший разряд целой части сдвигаются к младшему разряду до тех пор, пока у одного из чисел данные ссылки не совпадут (фактически, того же эффекта можно достигнуть, умножая оба числа на 10000, пока одно из них не станет целым, так как 0,16/0,04=16/4);
- Из делимого выделяется количество разрядов, равное количеству разрядов делителя (если изначально у делимого меньше разрядов, чем у делителя, целая часть будет равна нулю);
- Выполняется деление получившихся чисел;
- К делимому прибавляем старший из не использованных ранее разрядов и повторяем п.3;
- Когда число-делитель становится больше делимого, начинаем вычислять остаток: к делимому добавляем один пустой разряд (эквивалентно умножению на 10000) и производим деление;
- Повторяем п.5 до тех пор, пока не будет достигнута заданная точность или остаток не будет равен 0 (Рис. 4)
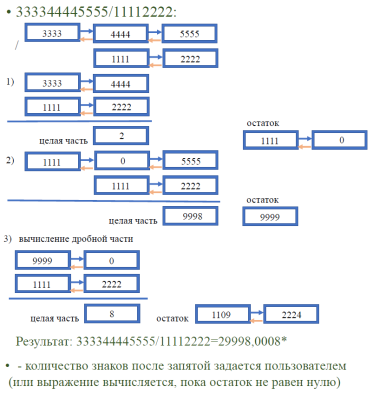
Рис. 4. Реализация операции деления
Возведение встепень
Возведение в степень путем последовательного умножения числа на само себя может привести к большому времени выполнения операции (особенно, если в показателе степени также длинное число). Чтобы этого избежать, был реализован алгоритм разложения показателя степени на множители:
- Если показатель степени четный, разделить показатель степени на два, выражение представить в виде a2n=an*an;
- Если показатель степени нечетный, то представить выражение в виде a2n+1=a2n*a, для a2n повторить шаг 1;
В результате выполнения такого алгоритма получится развернутая запись числа, которая громоздкая на вид, но дает колоссальный эффект при вычислении выражений типа an; Например, число a10 можно представить как ((a2)2*a)2. Программа выполнит фактически 4 операции умножения вместо десяти. В целом сложность такого алгоритма оценивается как О=log2n, где n — показатель степени, что гораздо эффективнее последовательного умножения (сложность алгоритма O=n);
Факториал
Факториал числа вычисляется путем рекурсивного умножения: n!=n*(n-1)! и т. д. Найти более быстрые алгоритмы для длинных чисел пока не удалось.
Пример применения алгоритма
Результатом проделанной работы стала программа, которая позволяет рассчитать выражение, содержащие до 27 переменных (которые могут повторяться внутри выражения) с расчетом результата, количество разрядов которого в десятичной системе может достигать 1010^9. Точность вычисления (количество знаков после запятой) задается пользователем. Над числами могут производиться все базовые арифметические операции (сложение, вычитание, умножение, деление, возведение в степень, факториал). Все функции для записи числа и выполнения расчетов вынесены в библиотеку, которую можно встроить в сторонний проект.
Пользователь может вводить выражение и переменные с клавиатуры. Также реализована возможность ввода выражения и переменных из файла, запись результата вычисления в переменную для последующего использования в новых выражениях, изменение выражения и значений переменных, сохранение выражений и переменных в файл.
Как уже было написано выше, сложно найти значение факториалов для чисел больших, чем 200. Данная программа позволяет рассчитывать факториал чисел до 6000 (Рис. 5).
Так как калькуляторов, рассчитывающих такие числа, найдено не было, в Интернете была найдена текстовая запись числа и результат был сверен посимвольно, так как вышло число, количество разрядов которого превышает 20 000 символов.
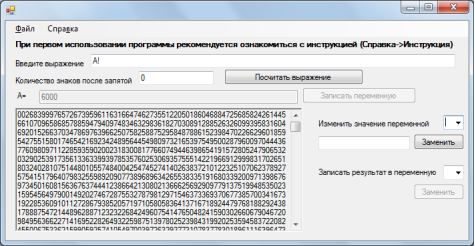
Рис. 5. Реализация возведения в факториал большого числа
Данная библиотека функций может послужить фундаментом для разработки более мощного калькулятора с более широкой областью применения. Целью разработки данной программы является возможность производить вычисления с абсолютно любой точностью, ограниченной лишь памятью компьютера, так как на данный момент предельная длина числа ограничена программно (1010:9 разрядов). Преодоление данного ограничения поможет перейти к арифметике произвольной точности.
Главной перспективой развития данного проекта является разработка калькулятора элементарных функций, в частности — тригонометрических. Для точного расчета тригонометрических величин и непериодических констант (например, числа Пи) можно использовать уже реализованные функции (сумма, деление, факториал), благодаря которым можно вычислить значение любой функции, составив ее ряд.
Следующей перспективой развития является более гибкая обработка выражений, которая позволит использовать произвольное количество переменных в выражении (на данный момент их количество ограничено буквами латинского алфавита).
Таким образом, на базе данной программы можно создать библиотеку функций, реализующих широкий набор математических операций с числами произвольной точности и бесконечной величины.
Литература:
- Электронные средства и системы управления: Материалы докладов Международной научно-практической конференции (13–16 октября 2010 г.). — Томск: В-Спектр, 2011: В 2 ч. — Ч. 2. — 178 с. ISBN 978–5-91191–223–6, С.123–129
- С. М. Окулов, Длинная арифметика, Информатика, 2016, № 5 (867), режим доступа: http://inf.1september.ru/2000/1/art/okul1.htm







