В настоящие время эллиптические кривые широко применяются в криптографии. Основным в арифметике на эллиптической кривой [1, c.31] является алгоритм умножения точки 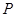 эллиптической кривой на числовую константу
эллиптической кривой на числовую константу 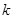 или алгоритм вычисления
или алгоритм вычисления 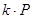 или алгоритм скалярного умножения точки. Поэтому актуальной становиться задача эффективной реализации скалярного умножения на эллиптической кривой. Проанализируем существующие методы скалярного умножения на эллиптической кривой.
или алгоритм скалярного умножения точки. Поэтому актуальной становиться задача эффективной реализации скалярного умножения на эллиптической кривой. Проанализируем существующие методы скалярного умножения на эллиптической кривой.
В данной статье мы рассматриваем эллиптическую кривую, 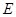 заданную уравнением в проективной системе координат
заданную уравнением в проективной системе координат 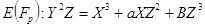 , где
, где 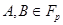 ,
, 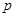 – простое число и
– простое число и  .
.
Базовыми алгоритмами для реализации скалярного умножения являются алгоритм сложения, удвоения точек, так как, если 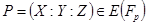 то
то 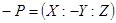 .
.
Алгоритм 1 [2, c. 102]. Сложения точек на эллиптической кривой заданных в проективной системе координат.
Вход 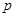 – простое число и точки
– простое число и точки 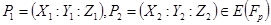 , где
, где 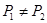 .
.
Выход: 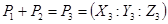
1 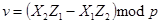
2 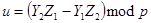
3 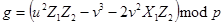
4 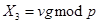
5 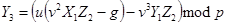
6 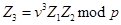
7 Return 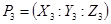
Алгоритм 2 [2, c. 102]. Удвоения точки на эллиптической кривой, заданной в проективной системе координат.
Вход 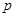 – простое число и точка
– простое число и точка 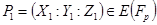 .
.
Выход: 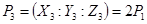
1 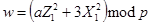
2 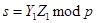
3 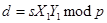
4 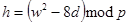
5 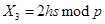
6 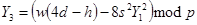
7 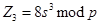
8 Return 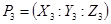
Приведем основные алгоритмы скалярного умножения 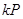 на эллиптической кривой, при их изложении будут использоваться следующие обозначения:
на эллиптической кривой, при их изложении будут использоваться следующие обозначения: 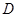 – сложность операции удвоения в группе точек эллиптической кривой;
– сложность операции удвоения в группе точек эллиптической кривой; 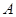 – сложность операции сложения-вычитания в группе; порядок точки
– сложность операции сложения-вычитания в группе; порядок точки 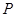 на эллиптической кривой
на эллиптической кривой 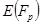 равен
равен 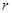 ;
; 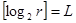 и число
и число 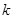 представлено в двоичной системе исчисления
представлено в двоичной системе исчисления 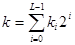 .
.
Алгоритм удвоения-сложения
Это один из самых простых методов, при котором вычисления осуществляются по формуле 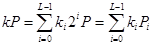 , где
, где 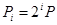 .
.
Вычисления осуществляются с помощью следующего алгоритма:
Алгоритм 3. Удвоения-сложения
Вход: 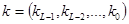 ,
, 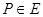
Выход: 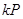 .
.
1. 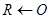
2. For 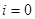 to
to 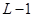 do
do
2.1 If 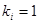 then
then 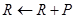
2.2 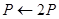
3. Return 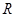
Реализация метода требует 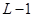 операций удвоения точки и
операций удвоения точки и 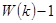 сложений, где
сложений, где 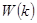 – вес Хэмминга двоичного вектора
– вес Хэмминга двоичного вектора 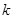 . Так как в среднем число единиц случайного вектора
. Так как в среднем число единиц случайного вектора 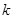 равно
равно 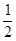 , то общее число групповых операций оценивается величиной
, то общее число групповых операций оценивается величиной 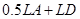 .
.
Алгоритм удвоения-сложения-вычитания
Модификация алгоритма удвоения-сложения, основанная на введении дополнительной операции вычитания точки. Например, число 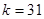 в двоичной системе имеет вес
в двоичной системе имеет вес 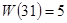 , но его можно представить как
, но его можно представить как 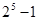 с весом
с весом 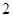 . Понижение количества операций происходит за счет понижения веса Хэмминга, так как число представляется в
. Понижение количества операций происходит за счет понижения веса Хэмминга, так как число представляется в 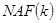 с коэффициентами
с коэффициентами 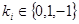 (NAF – non-adjacent form). Одно из свойств представления
(NAF – non-adjacent form). Одно из свойств представления 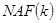 – отсутствие в нем смежных пар ненулевых элементов, благодаря чему возрастает удельный вес нулевых элементов
– отсутствие в нем смежных пар ненулевых элементов, благодаря чему возрастает удельный вес нулевых элементов 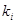 . Для расчета
. Для расчета 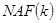 используется следующий алгоритм.
используется следующий алгоритм.
Алгоритм 4. Вычисления 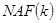
Вход: положительное целое число k.
Выход: 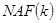 .
.
1 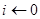
2 While 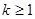 do
do
2.1 If 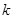 is odd then
is odd then 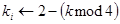 ,
, 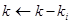
2.2 Else 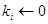
2.3 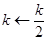 ,
, 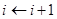
3 Return 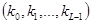
После расчета 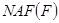 вычисляется точка
вычисляется точка 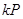 методом слева направо с
методом слева направо с
помощью следующего алгоритма.
Алгоритм 5. Удвоения-сложения-вычитания.
Вход: 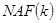 ,
, 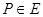
Выход: 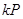 .
.
1 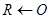
2 For 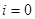 to
to 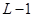 do
do
2.1 If 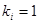 then
then 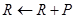
2.2 If 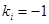 then
then 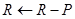
2.3 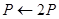
3 Return 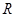
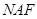 – представление числа
– представление числа 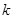 может оказаться на один бит длиннее
может оказаться на один бит длиннее
двоичного. В то же время для случайного 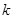 вероятность ненулевых элементов
вероятность ненулевых элементов 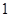 и
и 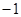 снижается от
снижается от 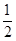 до
до 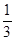 . Таким образом, в среднем для
. Таким образом, в среднем для 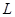 -разрядного числа количество групповых операций сложений-вычитаний оценивается как
-разрядного числа количество групповых операций сложений-вычитаний оценивается как 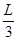 . Тогда общее число групповых операций оценивается как
. Тогда общее число групповых операций оценивается как 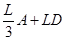 .
.
Метод окон с алгоритмом удвоения-сложения-вычитания
Если на компьютере есть резерв памяти, его можно задействовать для ускорения операции скалярного умножения на эллиптической кривой. В дальнейшем вместо точки 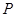 для вычисления можно использовать смежные блоки или окна шириной
для вычисления можно использовать смежные блоки или окна шириной 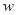 в
в 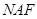 -представлении точки
-представлении точки 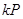 .
.
Назовем 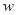 -окном числа
-окном числа 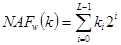 ,
, 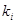 – нечетный коэффициент,
– нечетный коэффициент, 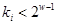 , содержащий хотя бы один ненулевой элемент. Заметим, что
, содержащий хотя бы один ненулевой элемент. Заметим, что 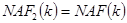 .
.
Пример. Пусть 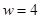 , тогда имеем
, тогда имеем 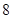 различных значений
различных значений 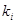 :
:
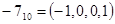
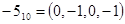
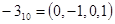
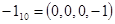
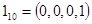
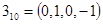
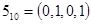
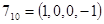
Этих окон достаточно для формирования числа произвольной длины 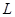 . Четные коэффициенты в
. Четные коэффициенты в 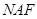 -представлении числа
-представлении числа 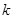 избыточны, так как они образуются удвоением нечетных. На первом этапе произведем вспомогательные вычисления и занесем в память
избыточны, так как они образуются удвоением нечетных. На первом этапе произведем вспомогательные вычисления и занесем в память 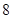 точек:
точек: 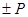 ,
, 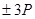 ,
, 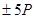 и
и 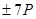 .
.
В общем случае в памяти хранится 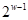 точек. Число
точек. Число 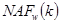 может быть определено с помощью модифицированного алгоритма 4. Модификация состоит в следующем: на шаге 2.1
может быть определено с помощью модифицированного алгоритма 4. Модификация состоит в следующем: на шаге 2.1 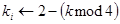 заменяется на
заменяется на 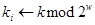 , где
, где 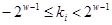 .
.
Алгоритм 6. Удвоения-сложения-вычитания.
Вход: 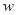 ,
, 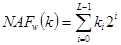 ,
, 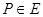 .
.
Выход: 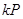 .
.
1 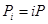 ,
, 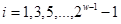 .
.
2 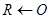
3 For 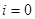 to
to 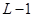 do
do
3.1 If 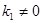 then If
then If 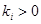 then
then 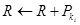 else
else 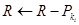
3.2 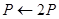
4 Return 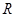
Например, 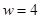 ,
, 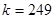 , при этом
, при этом 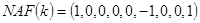 и
и 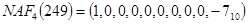 . Использование
. Использование 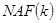 требует двух операций сложения точек, тогда как во втором случае за счет предварительного вычисления точки
требует двух операций сложения точек, тогда как во втором случае за счет предварительного вычисления точки 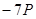 достаточно всего одного сложения. Число удвоений одинаково в обоих случаях.
достаточно всего одного сложения. Число удвоений одинаково в обоих случаях.
Реализуем предложенные методы скалярного умножения на языке программирования Free Pascal и кривыми из работы [3 c.6-8]:
Кривая P-192
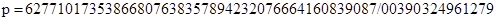
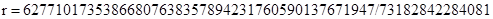
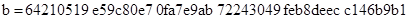
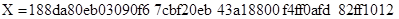
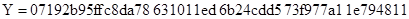
Кривая P-224

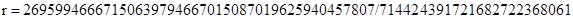
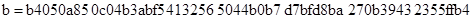
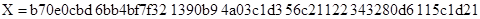
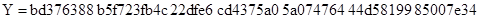
Кривая P-256
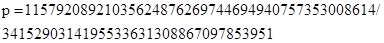
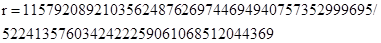

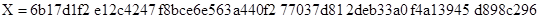
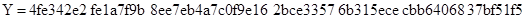 ,
,
где для всех трех случаев 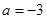 и точка
и точка 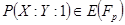 . Для тестирования алгоритмов скалярного умножения выбираем множество случайных целых чисел
. Для тестирования алгоритмов скалярного умножения выбираем множество случайных целых чисел 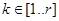 , содержащее 10000 элементов. После запросили системное время
, содержащее 10000 элементов. После запросили системное время 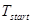 – время начала вычислений
– время начала вычислений 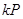 ,
, 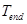 – время окончания выполнения алгоритма а среднее время вычисления скалярного умножения
– время окончания выполнения алгоритма а среднее время вычисления скалярного умножения 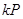 вычисляем по формуле
вычисляем по формуле 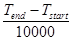 . Результаты, полученные при тестировании, представлены в таблице.
. Результаты, полученные при тестировании, представлены в таблице.
Таблица. Среднее время вычисления скалярного умножения в миллисекундах.
|
|
Кривая P-192 |
Кривая P-224 |
Кривая P-256 |
|
Алгоритм 3 |
5,897 |
6,724 |
7,550 |
|
Алгоритм 5 |
5,014 |
5,703 |
6,391 |
|
Алгоритм 6 |
4,978 |
5,539 |
6,217 |
Как видно из таблицы, время вычисления скалярного умножения на эллиптической кривой алгоритм 5 и алгоритма 6 отличается не слишком отличаются, но при этом алгоритм 5 не требует дополнительного свободного места на жестком диске. Следовательно, при построении криптосистемы, выбирая алгоритм для реализации скалярного умножения в случае если есть сводное место на жестком диске, лучше реализовывать алгоритм 6, иначе алгоритм 5.
Литература
1. Болотов А.А, Гашков С.Б., Фролов А.Б. Элементарное введение в эллиптическую криптографию: Протоколы криптографии на эллиптических кривых. – М.:КомКнига, 2006. – 280 с.
2. Бессалов А.В., Телиженко А.Б. Криптосистемы на эллиптических кривых : Учеб. пособие. – К: Политехника, 2004. – 224 c.
3. Recommended Elliptic Curves for Federal Government Use. .: http://csrc.nist.gov/groups/ST/toolkit/documents/dss/NISTReCur.pdf







