Разработка эффективной реализации алгоритмов выполнения арифметических операций с точками эллиптической кривой на базе приближенного метода в СОК

В статье исследуются методы выполнения арифметических операций с точками эллиптической кривой. Предложен метод модульного сложения чисел в системе остаточных классов с использованием приближенного метода, позволяющий без использования операции сравнения чисел в СОК вычислять значение модульного сложения целых чисел.

Ключевая слова: криптосистема на точках эллиптической кривой, система остаточных классов, модульное сложение, приближенный метод

Введение ипостановка задачи

В современном мире информационных технологий широкое применение находят электронные средства передачи, хранения и обработки данных. Преимущества, которые возникают при использовании современных информационных технологий для хранения, обработки и передачи данных накладывают риски: утери, кражи или несанкционированного использования данных. Для минимизации рисков широко используют облачные технологии совместно с криптографическими примитивами: схемами разделения секрета, симметричными алгоритмами шифрования и т. д.

Перспективным для построения надежной системы хранения и обработки данных является совместное использование схем разделения секрета для шифрования данных и ассиметричных систем шифрования для защиты и обновления секретных ключей шифрования данных используемых в схемах разделения секрета. Для защиты от технических сбоев, возникавших в облачных хранилищах данных эффективно используются схемы разделения секрета построенные на базе системы остаточных классов [1]. С целью минимизации издержек возникающих при использовании ассиметричных алгоритмов шифрования используем современные алгебраические структуры, построенные на базе аддитивной группы точек эллиптической кривой.

Эллиптическая криптография впервые была предложена учеными Коблицем и Миллером в 80 годы прошлого столетия. Однако, вопрос о применимости на практики эллиптической криптографии долгое время являлся не целесообразным так как вычислительная сложность алгоритмов выполнения арифметических операций с точками эллиптической кривой очень высокая по сравнению с аналогичными системами, работающими в конечных числовых полях. С другой стороны эллиптическая кривая позволяет обеспечить максимально возможную крипто стойкость теоретико-числовых систем из расчета на один бит размера задачи. Из-за высокого уровня крипто стойкости криптосистем, построенных на точках эллиптической кривой, было проведено множество исследований для понижения класса вычислительной сложности алгоритмов выполнения арифметических операций в группе точек эллиптической кривой. В результате проведенных исследований, были разработаны алгоритмы, позволяющие повысить эффективность алгоритмов выполнения арифметических операций с точками эллиптических кривых за счет использования расширенных чисел Мерсенна, которые в двоичном представлении количество бит равных одному меньше или равно пяти. В следствии, чего в конце XX — начале XXI веков началось активное использование эллиптической криптографии для обеспечения безопасности: США — FIPS 186–2-2000, Российской Федерация — ГОСТ P34.10–2012 и др.

Учитывая, что самыми алгоритмически сложными операциями в конечном поле являются операции «инверсия» и «нахождение остатка от деления на большое число». Применение для реализации арифметических операций с точками эллиптической кривой проективных координат позволяет уйти от операции «инверсия». Из всего выше следующего актуальность приобретает научная задача разработка алгоритма нахождения остатка от деления на основе приближенного метода в системе остаточных классов.

Для решения поставленной задачи следует решить следующие подзадачи:

1. Провести анализ алгоритмов выполнения арифметических операций с точками эллиптической кривой.
2. Разработать алгоритм нахождения остатка от деления в системе остаточных классов на базе приближенного метода.

Алгоритмы выполнения арифметических операций сточками эллиптической кривой

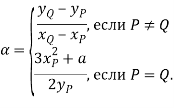
Для эффективной реализации арифметических операций с точками эллиптической кривой используют проективную систему координат, тогда точка эллиптической кривой задается а эллиптическая кривая имеет вид; .

Для перехода от проективной системы координат в аффинную систему координат используют, следующие формулы; , , где . Если , то точка в бесконечности и обозначается [2]. Использование малой теоремы Ферма и алгоритма быстрого возведения в степень позволяют вычислить операция инверсия в конечном поле , где .

Для уменьшения количества модульных операции для выполнения арифметических операций с точками эллиптической кривой используют модификацию проективные координаты Якоби [3]. Для перехода из проективной системы координат Якоби в аффинную систему координат используют, следующие формулы: 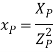, 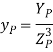. Тогда эллиптическая кривая в проективной системе координат Якоби имеет вид: . Точка в бесконечности имеет вид .

Удвоение точки эллиптической кривой в проективных координатах Якоби имеют вид;

,

,

.

Введем обозначения: -время выполнения модульного сложения целых чисел, - время выполнения модульного возведения в квадрат целых чисел, - время выполнения модульного умножения целых чисел, - время выполнения модульного умножения на константу целого числа. Тогда используя подход из работ [4, 5] удвоения точки эллиптической кривой в проективных координатах Якоби можно выполнить за время: , сложение точек за время: .

Методы вычисления умножения точки эллиптической кривой на скаляр

В основе криптографических алгоритмов построенных на точках эллиптической кривой является операция умножения точки эллиптической кривой на скаляр. Пусть задано фиксированное целое число в двоичном представлении: . Тогда задача формулируется зная точку и константу , вычислить . По аналогии с алгоритмом быстрого возведение в степень, можно вычислить умножение точки эллиптической кривой на скаляр используя алгоритм 1 удвоения-сложения [6].

Вход: целое число и точка .

Выход: точка .

1. ;
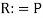2. For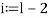downto 0 do
   1. ;
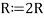   2. if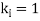then;
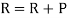3. Return .

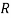Так как вычисления значения “” требует, только вычисления значения , то целесообразно использовать представление не в двоичном базисе а троичной системе (NAF-метод) , что позволить уменьшить длину на треть [7]. Для повышения производительности алгоритмов шифрования на точках эллиптической кривой используют метод окон из работы [8], который за счет предвычисленной последовательности значений позволяет рассматривать при вычислении не по одному биту как методе удвоения-сложения или NAF-метод а блоками заданного размера.

Метод нахождения остатка от деления чисел всистеме остаточных классов на базе приближенного метода всистеме остаточных классов

Базовыми операциями при реализации алгоритмов сложения и удвоения точек эллиптической кривой являются алгоритмы модульного сложения и умножения чисел. В работе [9] разработан эффективный метод выполнения модульного умножения чисел в СОК на базе приближенного метода. Разработаем алгоритм модульного сложения чисел.

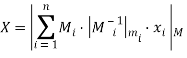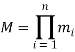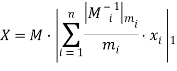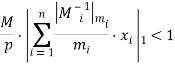Пусть число , где выполняется неравенство и модули СОК — попарно взаимно простые числа. Тогда согласно Китайской теореме об остатках , где , . Если использовать подход приближенных вычислений, тогда Китайскую теорему об остатках можно переписать в виде: , где -дробная часть числа. Тогда определения является ли неравенство , равносильно условию , следовательно . Использование данного факта позволяет эффективно определять необходимо ли из суммы вычитать модуль или нет, что позволяет эффективно реализовывать криптосистемы на точках эллиптической кривой.

Заключение

В работе проведено исследования алгоритмов выполнения арифметических операций в аддитивной группе точек эллиптической кривой, заданной над простым полем. Исследованы алгоритмы умножения точек эллиптической кривой на скаляр. Разработан алгоритм модульного сложения с помощью приближенного метода работает быстрее, чем рассмотренный аналогичные алгоритмы сравнения чисел в СОК. Работа выполнена при поддержки стипендии Президента РФ молодым ученым и аспирантам СП-1215.2016.5.

Литература:

1. Tchernykh A. et al. Towards Understanding Uncertainty in Cloud Computing with risks of Confidentiality, Integrity, and Availability //Journal of Computational Science. — 2016.
2. Bernstein D. J., Lange T. Faster addition and doubling on elliptic curves //International Conference on the Theory and Application of Cryptology and Information Security. — Springer Berlin Heidelberg, 2007. — С. 29–50.
3. Cohen H., Miyaji A., Ono T. Efficient elliptic curve exponentiation using mixed coordinates //International Conference on the Theory and Application of Cryptology and Information Security. — Springer Berlin Heidelberg, 1998. — С. 51–65.
4. Verneuil V. Elliptic curve cryptography and security of embedded devices: дис. — Université de Bordeaux, 2012.
5. Longa P., Miri A. Fast and flexible elliptic curve point arithmetic over prime fields //IEEE Transactions on computers. — 2008. — Т. 57. — №. 3. — С. 289–302.
6. Blake I. F., Seroussi G., Smart N. Elliptic curves in cryptography. — Cambridge university press, 1999. — Т. 265.
7. Reitwiesner G. W. Binary arithmetic //Advances in computers. — 1960. — Т. 1. — С. 231–308.
8. Järvinen K. Optimized FPGA-based elliptic curve cryptography processor for high-speed applications //INTEGRATION, the VLSI journal. — 2011. — Т. 44. — №. 4. — С. 270–279.
9. Chervyakov N. I. et al. Fast modular multiplication execution in residue number system //Quality Management, Transport and Information Security, Information Technologies (IT&MQ&IS), IEEE Conference on. — IEEE, 2016. — С. 30–32.