Методическая разработка урока геометрии в 8 классе на тему «Касательная к окружности»

Цели:

·           ввести понятие касательной, точки касания,

·           рассмотреть свойство касательной и её признак и показать их применение  в природе и технике.

Задачи урока:

Образовательные:

1.        Обеспечить овладение основными алгоритмическими приёмами построения касательной к окружности.

2.        Сформировать умения применять теоретические знания к решению задач.

Воспитательные:

1.        Развивать мышление и речь учащихся.

2.        Работать над формированием умений: наблюдать, подмечать закономерности, обобщать, проводить рассуждения по аналогии,

3.        Привитие интереса к математике.

Практические:

1.      сформировать умение строить касательную к окружности.

2.      рассмотреть применение в природе и технике.

Тип урока: комбинированный.

Ход урока:

I. Организационный момент (1 мин)

II. Актуализация знаний (2 мин): Учитель задает учащимся вопросы.

Что такое окружность, радиус, диаметр, хорда окружности? Прямая?  Как, вы, думаете, каково взаимное расположение этих фигур?

III. Объявление темы урока (1мин)

Тема урока: Касательная к окружности. Что мы должны будем узнать? Этот урок мы посвятим изучению свойства касательной к окружности, научимся строить её, а также научимся применять теоретические знания к решению задач.

IV.Работа индивидуальная и в парах (3мин).

Постройте в тетради окружность произвольного радиуса r и прямую.

 

 

 

 

 

 

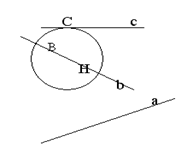
Рис. 1.

Ответьте на вопрос: сколько общих точек могут они иметь и от чего это зависит?

V Сообщение целей и задач (1мин).  Какая цель нашего урока?

Ребята пытаются сформулировать цель    работы.

VI.Планирование (2мин.)

У нас с вами на изучение новой темы 2 варианта:

1                    Самостоятельная работа с текстом учебника (конспект), совместное выполнение заданий по уровням, самостоятельная работа;

2. Совместная работа с учителем (исследование, запись вывода в виде таблицы, доказательство теорем), выполнение заданий по уровням, самостоятельная работа

Пусть d- расстояние от центра окружности до прямой

Заполните таблицу:

Таблица 1

Взаимное расположение прямой и окружности

	d < r	d > r	d = r
рисунок
Общее количество точек	2 общие точки	1 общая точка	нет общих точек
Название прямой	секущая	касательная	--

 

VII. Практическая деятельность учащихся (18 мин).

Определение. Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка, называется точкой касания прямой и окружности.

Учащиеся называют на рисунке точку касания и прямую - касательную к окружности.

(C- точка касания, прямая с – касательная к окружности). Все это фиксируется в тетрадях учащихся.

Учитель: Какими же свойствами обладает эта прямая? Чтобы ответить на этот вопрос, проведите отрезок соединяющий центр окружности и точку касания, измерьте получившийся угол.

Ученики измеряют получившийся угол. (90)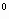

Учитель: Что можно сказать о касательной и радиусе?

Учащиеся: Они перпендикулярны.

Теорема(свойство касательной): Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

 

 

 

 

 

 

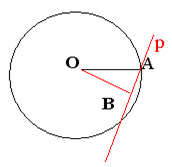
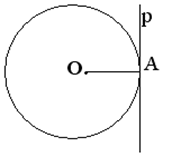Рис.2.а                                                              Рис.2.б

Допустим, что прямая р не перпендикулярна к радиусу ОА (На рисунке сделать построение другим цветом). Сравните расстояние от центра окружности до прямой р с радиусом окружности.

Назовите перпендикуляр к прямой р (ОВ) и наклонную (ОА)

Ученики называют перпендикуляр к прямой и наклонную.

Учитель: Расстояние от точки О до прямой р, это ОВ, меньше радиуса окружности ОА, который в данном случае будет являться наклонной по отношению к прямой р, а расстояние от точки О до прямой р – перпендикуляр, а, как известно, любая наклонная больше перпендикуляра, проведённого из той же точки к той же прямой, т. е. ОВ<ОА.

Учитель: Сколько тогда общих точек у прямой р и окружности?

Учащиеся: 2

Учитель: Может ли прямая р быть касательной к окружности? Почему?

Учащиеся: Т.к. прямая р имеет две общие точки с окружностью, то она не может быть касательной по определению.

Учитель: Верно ли предположение, что прямая р не перпендикулярна радиусу окружности? О чём это говорит?

Учащиеся: Предположение не верно, следовательно прямая р перпендикулярна радиусу ОА.

Теперь запишем это доказательство в тетради.

Дано: окр. (О; r=ОА), р-касательная к окружности, А-точка касания.

Доказать: р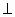ОА.

Доказательство: Предположим, что р не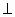ОА, тогда ОА наклонная к прямой р, а ОВ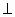р, т. к. ОВ<ОА, то расстояние от центра окружности О до прямой р меньше радиуса, следовательно прямая р и окружность имеют две общие точки, что противоречит условию: прямая р – касательная, т. о. р 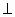ОА. Теорема доказана.

Задача 1.

Через точку лежащую на окружности провести касательную.

Построение:

1. Проведем радиус к точке А, ОА
2. Построим прямую р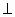ОА

Решить устно №631(б,г,д)

1.                 «3» - №633(ОА) ,640

2.                 «4» - №633(АВ), 641

3.                 «5» - №633 (АС), 638.

VIII. Осуществление контроля (9 мин).

 

 

 

 

 

 

 

 

 

 

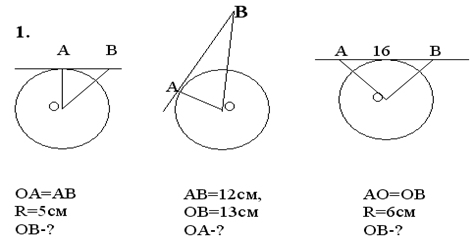Рис. 3. Самостоятельная работа.

Дополнительное задание: На касательной к окружности от точки касания по обе стороны от неё отмечены две точки М и Т, удаленные от центра окружности на расстояние, равное 20см; ТМ=32 см. Найдите радиус окружности.

IX.Оценивание учащихся (1 мин)

 Ответы:5√2; 5; 10

Х. Итог урока (5 мин).

А) История появления касательной: Понятие касательной – одно из древнейших в математике. Интерес к касательным возродился в Новое время. Тогда были открыты кривые, которых не знали учёные древности. Например, Галилей ввёл циклоиду, а Декарт и Ферма построили к ней касательную.

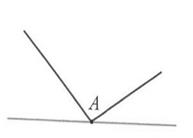В первой трети XVII в. начали понимать, что касательная – прямая, «наиболее тесно примыкающая» к кривой в малой окрестности заданной точки.  Легко представить себе такую ситуацию, когда нельзя построить касательную к кривой в данной точке (смотри Рис. 4) .

 

 

 

 

 

          Рис. 4. Пример прямой, не являющейся касательной.

Б) Применение: Колесо велосипеда - окружность, спицы – радиусы окружности, касательная – дорога.

В) Рефлексия

Ответить на вопросы:

На уроке было:

1.интересно

2.скучно

3.безразлично

 

Я на уроке

1.работал

2.отдыхал

3.помогал другим

 

Итог

1.понял материал

2. узнал больше, чем знал

3. не понял

ХI. Домашнее задание (2 мин):

На «3» №631,(а,в),635,637

На «4» №631,(а,в), 637

На «5» №643,644

 

Литература:

1.      Геометрия: 7 – 9 кл. / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. — М.: Просвещение, 2004—2011.

2.      Лукичева Е.Ю. Особенности обучения математике в контексте содержания ФГОС: учебно-методическое пособие – СПб.: СПб АППО, 2013

3.      Стройк Д.Я. Краткий очерк истории математики/ Д. Я. Стройк. — М.: Наука, 1978