Цель: формирование представлений у обучающихся о понятиях окружности и круга; формирование умения строить окружность с помощью циркуля по заданному радиусу и диаметру.
Тип урока: урок «открытия» нового знания
Задачи:
Обучающие: формировать теоретическое и практическое представление об окружности и круге, как о геометрических фигурах, их элементах; сформировать умение применять изученные понятия для решения задач практического характера.
Развивающие: развивать логическое мышление для сознательного восприятия учебного материала, внимание, зрительную память, грамотную математическую речь.
Воспитательные: воспитание познавательной активности, положительной мотивации к изучению предмета.
Результаты:
Предметные: имеют представление о таких понятиях как «окружность» и «круг», их элементах; применяют полученные знания при решении практических задач.
Метапредметные: отбирать информацию, полученную из разных источников, выделять и формулировать познавательную цель, планировать общие способы работы.
Личностные: развивать креативность мышления, инициативу, находчивость, активность при решении математических задач.
ХОД УРОКА:
1 Этап. Организационный момент. (1 мин)
Приветствие, проверка подготовленности к учебному занятию, организация внимания детей.
2 Этап. Постановка учебной задачи. (7 мин)
-Откройте тетради, запишите на полях сегодняшнее число 16.12.16.
-Отступите от домашней работы 5 см и поставьте в центре произвольную точку О.
-Отметьте 4 точки, удаленные от точки О на 2 см.
-Сколько еще таких точек можно отметить?
-Отметьте их.
-Если мы соединим эти точки между собой, какую фигуру мы получим?
-Правильно, Окружность!
Заштриховать окружность и спросить:
- Как вы думаете, как называется фигура, которую я заштриховала?
- Правильно, круг!
- Какая у нас сегодня будет тема урока? «Окружность и круг», запишите её в тетрадь.
- А как вы думаете, какие у нас сегодня цели урока?
3 Этап. Построение проекта выхода из затруднения детьми (открытие нового знания) (20 мин)
- Начертите у себя в тетради окружность радиусом 3 см с помощью циркуля. Иголку циркуля ставим на центр окружности, вторую ножку вращаем вокруг центра окружности.
- У всех получилось? Кто не справился?
- Откройте учебник на странице 143, тут даны вопросы к параграфу.
- Найдите ответы на эти вопросы и отметьте их карандашом в учебнике, на эту работу у вас 15 минут.
4 этап. Реализация проекта. (7 мин)
Провести опрос по найденным ответам. Помочь найти ответы тому, кто не справился.
Вопросы:
- Как расположены точки окружности относительно её центра?
- Какой отрезок называют радиусом окружности?
- Какой отрезок называют хордой окружности?
- Какую хорду называют диаметром окружности?
- Как связаны между собой диаметр и радиус окружности?
- Как называют части, на которые две точки делят окружность?
- Как называют окружность и часть плоскости, которую она ограничивает?
- Как называют части, на которые два радиуса делят круг?
- Какую фигуру называют полукругом?
5 Этап. Первичное закрепление знаний во внешней речи (25 мин)
Выполнение заданий на применение полученных знаний. Начинают на 1 уроке, продолжают на 2.
Номера: 699-702 (устно), 704-709 (письменно и у доски).
6 Этап. Самостоятельная работа (15 мин)
Задание №1:
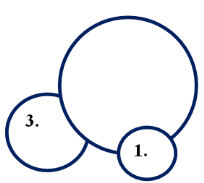
Рис.1
Измерьте радиусы окружностей, изображённых на рисунке (рис.1.)_____________
Запишите, чему равны диаметры каждой из фигур____________________________
Запишите, какие выводы вы сделали?______________________________________
Задание №2:
Нарисуйте окружность произвольного радиуса. Изобразите все изученные вами элементы окружности и подпишите их.
Задание №3:
Нарисуйте две окружности, которые не пересекаются. Измерьте длины их радиусов, расстояние между их центрами. Полученные результаты обсудите с соседом по парте. Запишите вывод.
Задание №4:
Нарисуйте две окружности, которые имеют одну общую точку. Измерьте длины их радиусов, расстояние между их центрами. Полученные результаты обсудите с соседом по парте. Запишите ваш вывод.
7 Этап. Рефлексия деятельности (5 мин)
- Ребята, какая сегодня была тема урока?
- Что нового узнали на уроке?
- Что вы научились сегодня делать?
- Возникли ли у вас трудности при изучении этой темы?
Запишите домашнее задание в дневник: 707, 710, на альбомном листе нарисовать рисунок, состоящий только из окружностей.
Литература:
- Математика: 6 класс: учебник для учащихся общеобразовательных организаций/ А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. – М.: Вентана-Граф, 2014.-304с. : ил.







