Рассматривается динамическая система, описываемая уравнениями
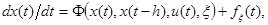
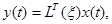
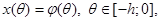
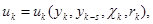(1)
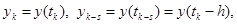
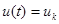при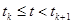 
,
где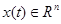 
— вектор состояния объекта управления (ОУ); 
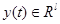— вектор выхода; 
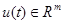— вектор управляющих воздействий; 
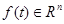— вектор возмущающих воздействий; 
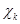— матрица настраиваемых коэффициентов регулятора; 
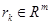— вектор задающих воздействий; 
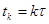— дискретный аналог времени; 
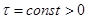— шаг дискретизации; 
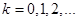— номер шага; 
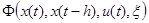— отображение, удовлетворяющее условиям существования и единственности решения уравнений (1) при заданной начальной вектор-функции 
; 
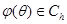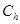— пространство непрерывных функций; 
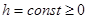— запаздывание; 
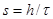— число тактов запаздывания; 
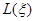— матрица выхода; 
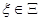— набор неизвестных параметров; 
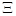— известное множество возможных значений 
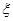. Требуется построить адаптивную систему управления таким образом, чтобы при любом наборе 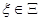, при любых начальных условиях 
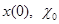и возмущениях 
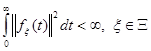выполнялось одно из следующих целевых условий:
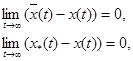(2)
совместно с условием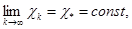 
(3)
где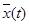 
— вектор состояния явной эталонной модели (ЭМ); 
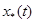— вектор состояния неявной ЭМ. Если же на ОУ действует неконтролируемое, ограниченное по норме возмущающее воздействие 
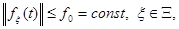то условия (2) заменяются на следующие:
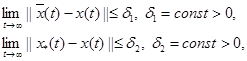
а условие (3) — на предельное соотношение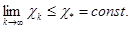 
Решение задачи синтеза системы (1) включает в себя следующие этапы: представление исходной системы в эквивалентной форме, а именно в виде линейного стационарного блока прямой цепи и нелинейного нестационарного блока обратной связи (1 этап); обеспечение строгой положительности передаточной матрицы линейной части системы (2 этап); построение дискретных алгоритмов настройки коэффициентов регулятора (3 этап); проверка выполнения целевых условий и свойств адаптивности системы (4 этап); упрощение технической реализации гибридной системы управления (5 этап).
При этом на 2 и 3 этапах построения адаптивной системы выделяется непустой класс гиперустойчивых систем, допускающий существенное расширение за счет применения нелинейного преобразования элементов вектора состояния исходной системы. С этой целью используются результаты, полученные в рамках теории непрерывных групп Ли, позволяющие для системы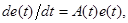 
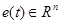построить формы q-й степени, служащие элементами вектора 
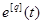расширенного пространства состояний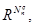 
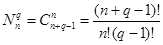и обеспечивающие выполнение условия 
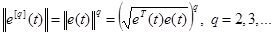при специально организованном базисе.
Данный подход используется для выделения расширенного класса гиперустойчивых систем с помощью модификации неравенства Попова, представленного следующим образом: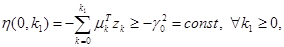 
где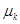 
— преобразованный вектор управления; 
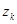— нелинейно преобразованный вектор выхода, явный вид которого уточняется на 3 этапе синтеза гибридных систем адаптации.
Результаты имитационного моделирования показывают, что большинство, построенных с помощью данного метода, систем управления обладают удовлетворительным качеством работы при произвольных наборах 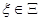и наличии внешних помех.
Литература:
1. Еремин Е. Л., Шевко Д. Г. Алгоритмы и S-моделирование гибридных систем адаптации // Динамические модели и S-моделирование систем / Е. Л. Еремин. — Благовещенск, 2003. — С. 282–307.
2. Еремин Е. Л., Шевко Д. Г. Гибридная нелинейно преобразованная система прямого адаптивного управления // Радиоэлектроника, информатика, управление. — 2002. — № 2(8). — С. 142–147.
3. Еремин Е. Л., Шевко Д. Г. Дискретная нелинейно преобразованная система прямого адаптивного управления с явной эталонной моделью // Вестник Амурского государственного университета. — 2001. — № 15. — С. 15–18.
4. Еремин Е. Л., Шевко Д. Г. Имитационное моделирование технически эквивалентных гибридных систем управления // Информатика и системы управления. — 2001. — № 2. — С. 36–42.
5. Еремин Е. Л., Шевко Д. Г. Методика синтеза гибридных нелинейно преобразованных систем прямого адаптивного управления на основе критерия гиперустойчивости // Вестник Амурского государственного университета. — 2003. — № 23. — С. 24–27.
6. Еремин Е. Л., Шевко Д. Г. Нелинейно преобразованные алгоритмы гибридной системы управления непрерывным объектом // ММТТ. — 2003. — Т. 2. — С. 69–70.
7. Еремин Е. Л., Шевко Д. Г. Синтез и упрощение технической реализации гибридной нелинейно преобразованной системы прямого адаптивного управления // Вычислительные технологии. — 2003. — Т. 8, № 3. — С. 47–57.
8. Еремин Е. Л., Шевко Д. Г. Эквивалентность технической реализации гибридных систем прямого адаптивного управления // ММТТ. — 2002. — Т. 2. — С. 22–23.
9. Островерхий В. В., Шевко Д. Г. Задачи, решаемые автоматической системой управления шасси гусеничной машины // Вестник Амурского государственного университета. Серия: Естественные и экономические науки. — 2011. — № 53. — С. 69–73.
10. Шевко Д. Г. Алгоритмы настройки для гибридной системы управления с запаздыванием // Молодой ученый. — 2014. — № 19. — С. 262–263.
11. Шевко Д. Г. Гибридная система прямого адаптивного управления неминимально-фазовым объектом // Информатика и системы управления. 2002. № 1(3). С. 112–120.
12. Шевко Д. Г. Критерий гиперустойчивости и синтез нелинейно-преобразованных гибридных систем прямого адаптивного управления // Вестник Амурского государственного университета. Серия: Естественные и экономические науки. — 2012. — № 57. — С. 65–69.
13. Шевко Д. Г. Модели и алгоритмы нелинейно преобразованных гибридных систем прямого адаптивного управления: автореф. дис. … канд. техн. наук. — Хабаровск, 2003. — 20 с.
14. Шевко Д. Г. Синтез алгоритмов самонастройки регулятора дискретной системы управления и сравнительный анализ качества процессов адаптации // Информатика и системы управления. — 2001. — № 1. — С. 97–105.
15. Шевко Д. Г. Синтез и нелинейные преобразования гибридных систем прямого адаптивного управления // Информатика и системы управления. 2002. № 2(4). С. 133–144.
