В работе обсуждается применение некоторых форм в отношениях между «учитель-ученик» прямой и обратной связи с целью упрощения обучения математики в средней школе.
Ключевые слова: график ломаной функции, график целой функции, период функции, дробная часть.
Согласно требованиям современного периода важное место при обучении занимают интерактивные методы обучения (ИМО). Использование этих методов развивает интенсивность процесса обучения, преобразовывает урок в интенсивную и продуктивную деятельность. ИМО способствуют свободному размышлению у учеников, позволяют свободному высказыванию мнений. При решении задач (проблем) учитель и учащиеся размышляют над данной задачей, и между ними возникает систематическая связь. Они стараются преодолевать трудности, которые возникают при взаимной деятельности. Все это оказывает влияние на развитие процесса обучения.
Одной из особенностей активного обучения является направляющая роль преподавателя. При активном обучении, в отличие от традиционного обучения, учащиеся активно усваивают знания, информацию. При использовании ИМО у учащихся развивается исследовательская деятельность, в последовательной форме систематизируются знания, не заданные в готовом виде, формируется подход к решениям данной проблемы. При современном обучении преподаватели должны отвыкнуть от принципа «запомни». У учащихся должны усиливаться желание учиться, развиваться мышление, деятельность, должны самостоятельно приобрести знания.
В условиях активного обучения особое внимание уделяется развитию связи «учитель-ученик», в процессе подготовки уделить особое внимание тому, как поставлена проблема (задача). Задача должна быть поставлена в такой форме, чтобы ученики при решении данной задачи могли найти вывод в более простом и запоминающемся виде. На уроках математики учитывается последовательность усваивания знаний, а также процесс перехода упражнений от простого к сложному. Вспомогательные вопросы, заданные учителем, должны способствовать быстрому решению задач учениками. Задача, поставленная на уроках математики должна соответствовать уровню класса и быть простой на вид. Она должна быть поставлена так, чтобы при ее решении возникли новые интересные вопросы и ответы на эти вопросы. Желательно, чтобы на уроках математики этот процесс возник в начале урока.
В свою очередь, этот процесс должен строиться так, чтобы он послужил анализу результата, преподнесению информации, упрощению оценивания. Желательно, чтобы у каждого учителя были сложные задания, и решение сложных заданий устранило трудность последующих уроков. Решение этих трудных заданий должно служить развитию у ученика ответственности к самому себе и усвоению знаний в свободном виде [1].
Желательно, чтобы ученик знал, что он изучает дополнительно на уроке. Например: Говоря о прямой линии, находящаяся на ней точка относится к первым понятиям, а взаимное расположение прямых линий способствует условию последующих понятий (треугольник, четырехугольник и т. д.). формирование связи с учениками должно преобразоваться в такую форму образования, чтобы у них сформировалась самоуверенность. В вышеуказанных процессах роль учителя велика. Если в классе ученики обладают слабыми знаниями, значит методы преподавания учителя очень слабые.
Учитель играет вспомогательную роль, способствует ускорению усваивания знаний, помогает систематизированию приобретенных знаний, в классе играет роль координатора.
В этот момент главным оружием учителя должно быть ИМО. При использовании этих методов не должны быть ненужные вопросы и обсуждения. Неправильно требовать у ученика точное объяснение решения задач или заданий. Если ученик умеет применять полученные знания в решениях поставленных задач или заданий, то это говорит о достижении учителя!
На уроках по математике, где используются активные методы обучения, ученики должны быть самостоятельны, не должны повторять мнения других учеников, способные ученики могут выявить свои потенциальные возможности, не вызывая ревность.
Например [2], [3]:
Предмет: Начало алгебры и анализа.
Тема: Функции 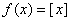 и
и 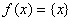 и их графики (рекомендуется преподавание урока в течении 2-х часов).
и их графики (рекомендуется преподавание урока в течении 2-х часов).
Стандарт: 2.2.4, 2.2.3.
2.2.4 — Проводит вычисления, подставляя значения переменных в формулы.
2.2.3 — Строит графики функций на основе данных формулы.
Ожидаемые результат обучения:
- находит область определения и область изменения функций;
- исследует существование периода функции;
- умеет вычислять с помощью подстановки значения выражения, заданного с помощью формулы, вместо значения переменных;
- умеет строить графики функций;
- показывает отношение к представлениям учеников.
Форма работы: коллективная работа, групповая работа.
Способ работы: мозговая атака, обучения.
Ресурсы: Учебник, рабочие листы, компьютер, проектор.
Ход урока
Мотивация: После организации класса составляю мотивацию
следующим образом.
Вешаю два рисунка на доску, как показано, и поручаю дополнить предложения.

Ученики дополняют предложения в течении 2–3 минут.
1) Целая часть числа — это наибольшее целое число, которое не больше самого числа (это утверждение вытекает также из свойства числовой оси: На числовой оси каждое число больше числа, стоящего левее от него, и меньше числа, стоящего правее от него).
2) Дробная часть числа принимает значение в интервале 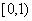 .
.
Задаю вопрос ученикам: Почему дробная часть отрицательных чисел есть положительное число?
Объяснение: Пользуясь формулами 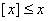 и
и 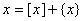 для любого числа
для любого числа 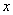 находим
находим 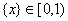 из
из 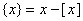 .
.
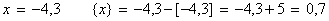
Исследование
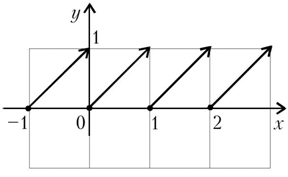
Разделив класс на 2 группы, поручаю одной группе построить график функции 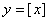 , другой группе построить график функций
, другой группе построить график функций 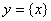 .
.
После построения графиков поручаю им найти свойства, которыми обладают графики.
1 группа: (целая функция) 2 группа: (ломанная функция)
Полученные результаты 1-ой группой:
а) при 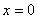
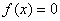 , и график функции проходит через начало координат;
, и график функции проходит через начало координат;
б) при любом значении 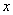
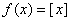 имеет значение. Значит
имеет значение. Значит 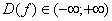 ;
;
в) при любом значении 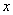
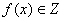 ;
;
г) 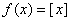 — не периодическая функция. Для
— не периодическая функция. Для 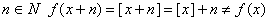 ;
;
д) график функции 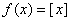 ломанный.
ломанный.
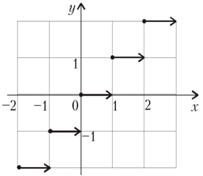
Полученные результаты 2-ой группой:
а) при 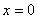
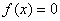 , и график функции проходит через начало координат;
, и график функции проходит через начало координат;
б) при любом значении 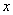
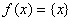 имеет значение. Значит
имеет значение. Значит 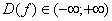 ;
;
в) при любом значении 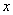
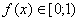 ;
;
г) 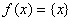 — периодическая функция и
— периодическая функция и 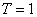 . Для
. Для 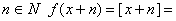
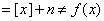 ;
;
д) график функции 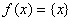 ломанный.
ломанный.
Обмен информации. График каждой группы передается другой группе. После рассмотрения графиков 1 член из каждой группы преподносит исследованную работу, затем перечисляются результаты.
Обсуждение информации. После перечисления результатов обсуждаются результаты и правильность построения графиков.
Для обобщения и обсуждения темы задаю 4 упражнений, затем проверяю правильность решений.
Упражнения:
1. Найдите значения этих выражений: а) 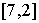 ; б)
; б) 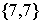 ; в)
; в) 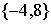 ; г)
; г) 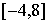 .
.
2. Укажите несколько чисел, целая часть которых а) 8; б) -1; в) 10.
3. Укажите несколько отрицательных чисел, дробная часть которых
а) 0,3; б) 0,57; в) 0,01;
4. Найдите период функции 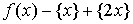 .
.
После решения упражнений разделяю класс на 3 группы, затем с помощью компьютера и проектора задаю им упражнения.

Самостоятельные работы решаются, и лидеры каждой группы представляют свои работы. После этого со всем классом проводится обсуждение темы. Затем ученики, пользуясь своими знаниями, перечисляют новые, приобретенные знания.
Оценивание: применение, описание и по представлению
|
I уровень (3. три) |
II уровень (4.четыре) |
III уровень (5.пять) |
|
Подставляет значения в формулы данных функций и находит значение функции с помощью учителя |
Подставляет значения в формулы данных функций и находит значение функции |
Подставляет значения в формулы данных функций и находит значение функции; находит область определения |
|
Не умеет строить график данной функции |
Строит график данной функции |
Строит график данной функции и на основе этого графика перечисляет свойства функции |
|
Применяет данные знания решению упражнений с помощью учителя |
Самостоятельно применяет данные знания решению упражнений |
Самостоятельно применяет данные знания решению упражнений и объясняет решенное упражнение |
Для творческого применения даю следующее уравнение как домашнее задание:
Решите квадратичное уравнение 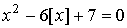 .
.
Положим 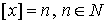 , так как
, так как 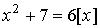 .
. 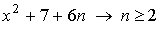 .
.
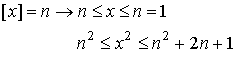
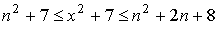 (1)
(1)
Если в (1) сделать замену 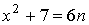 , то
, то
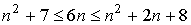
1. 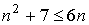
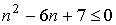
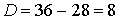
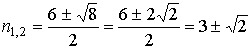
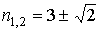
2. 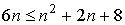
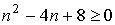
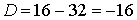 не имеет действительных корней.
не имеет действительных корней.
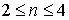
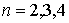
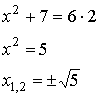
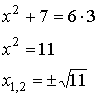
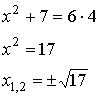
Корни этого уравнения: 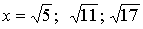 .
.
Проверка:
1) 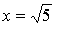 2)
2) 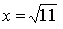 3)
3) 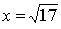
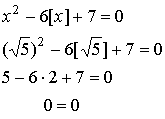
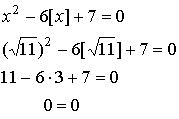
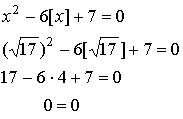
Литература:
1. Kurikulum jurnalı, Bakı, 2012-ci il, № 3, 152 s.
2. Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. М.:«Мир»,1998.703 с.
3. М. К. Потапов, В. В. Александров, П. И. Пасиченко. Алгебра и начала анализа. // АО Столетие, 1996.







