В данной статье дается один из путей изучения понятия «Производной», на доступном для учащихся языке составляется математическая модель физического процесса, представление этой модели в виде математического понятия и интерпретация этого понятия. Подробно рассматривается применение нового понятия для вывода формул.
Ключевые слова: методика, пути изучения, понятие производной, приращение аргумента, приращение функции, геометрический смысл, физический смысл, алгоритм.
Одной из важных побудительных сил учения является мотив достижения успеха. По словам Сухомлинского «интерес к учению есть только там, где есть вдохновение, рождающееся от успеха».
Нужно на каждом уроке, для каждого ученика создавать ситуацию успеха, сущность которой заключается в том, что каждый ученик работает на уровне своих возможностей, позволяющих ему справляться с предъявленными к нему требованиями.
Посильные трудности вырабатывают у учащихся положительную мотивацию учения, позволяют превратить учение из принудительного в добровольное.
Для достижения желаемого результата учитель должен создать на уроке такую ситуацию, использовать такие методы и средства обучения, которые были бы интересны ученику, располагали бы его к совместной деятельности, активизировали бы его учение.
Только там, где царят творческий труд, взаимное доверие, учителю легко работать, а ученику радостно жить.
В своей работе показан методический подход к процессу обучения именно с этой позиции.
При переходе из среднего звена обучения в старшее, когда начинается изучение «алгебры и начала анализа» в 10 классе, учащиеся испытывают достаточно большие трудности. Этой касается и основной темы данного курса — «Производная».
Целью данной методической разработки является оказание помощи учащимся в преодолении этих трудностей. Особенностью учебного материала это наглядное, доступное и достаточно научное изложение понятия «производной».
Опыт показывает, что относительно нетрудно научить учащихся формулировать определение производной, вычислять производную, находить производную функции в точке, пользуясь основными правилами дифференцирования. Не вызывает особых затруднений и применение производной к исследованию функции. А для этого в самом начале изучения темы следует найти правильный путь введения производной, ввести на доступном уровне учебный материал. Если учащийся сумеет применить определение производной для ее нахождения, показать геометрический и физический смыслы, то можем сказать, что он сможет и в дальнейшем видеть ее в различных приложениях, в физике, химии, биологии и т. д.
Вводная часть
Представим себе, что мы отправляемся в автомобильную поездку. Садясь в машину, посмотрим на счётчик километража. Теперь в любой момент времени мы сможем определить путь, пройденный машиной. Скорость движения мы узнаем по спидометру. Таким образом, с движением автомобиля, как и с движением любой материальной точки, связаны величины — путь S и скорость V, которые являются функциями времени t.
Ясно, что путь и скорость связаны между собой количественными характеристиками.
В конце XVII века английский учёный Исаак Ньютон открыл общий способ описания этой связи. Это открытие стало поворотным пунктом в истории естествознания. Оказалось, что связь между количественными характеристиками многих процессов, исследуемых физикой, химией, биологией, техническими науками, аналогична связи между путём и скоростью.
Основными математическими понятиями, выражающими эту связь, являются производная и интеграл.
Построенная Ньютоном модель механического движения остаётся самым важным и простым источником математического анализа, изучающего производную и её свойства. Вот почему на вопрос, что такое производная, короче всего ответить так:
Производная — это скорость, это скорость изменения функции.
В учебнике производная функции в точке х определяется как предел разностного отношения
![]() =f'(х)
=f'(х)
Также определён предел функции при х→0 т. е.
y=
Поэтому необходимо ввести понятие предела на нескольких простых задачах.
Пример 1:
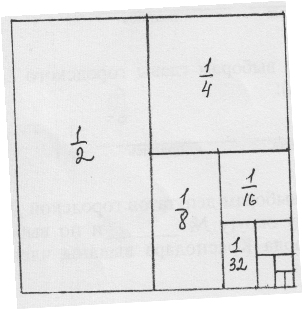 Дан квадрат со стороной 1. Разделим его пополам, затем половину пополам, затем четверть пополам, и т. д., получим последовательность чисел
Дан квадрат со стороной 1. Разделим его пополам, затем половину пополам, затем четверть пополам, и т. д., получим последовательность чисел ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() и т. д. Вычислить предел, к которому стремится сумма всех членов этой последовательности.
и т. д. Вычислить предел, к которому стремится сумма всех членов этой последовательности.
Данная последовательность сходящаяся, её члены составляют бесконечно убывающую геометрическую прогрессию. Эти понятия и сумму бесконечно убывающей геометрической прогрессии изучаем в 9 классе. По чертежу легко видеть, что сумма чисел ![]() +
+ ![]() +
+ ![]() +
+ ![]() + … в целом даёт 1, т. к. если заштриховать все получившиеся прямоугольники, то получится весь квадрат, площадь которого равна 1. Значит предел, к которому стремится сумма всех данных дробей, при неограниченном увеличении знаменателя есть число 1.
+ … в целом даёт 1, т. к. если заштриховать все получившиеся прямоугольники, то получится весь квадрат, площадь которого равна 1. Значит предел, к которому стремится сумма всех данных дробей, при неограниченном увеличении знаменателя есть число 1.
Подобного рода примеры поясняют учащимся предел числовой последовательности.
Вернёмся к движению. Представим себе любой движущийся предмет материальной точкой. Пусть данная материальная точка движется по прямой по определённому закону, выражающему зависимость S как функцию от времени. Рассмотрим отрезок времени [![]() ]. Определим среднюю скорость движения материальной точки на данном отрезке как отношение пройденного пути к продолжительности движения:
]. Определим среднюю скорость движения материальной точки на данном отрезке как отношение пройденного пути к продолжительности движения:
Для определения скорости движения точки в момент времени t (её в механике часто называют мгновенной скоростью) поступим так: возьмём отрезок времени [t; ![]() ], вычислим среднюю скорость на этом отрезке и начнём уменьшать отрезок [t;
], вычислим среднюю скорость на этом отрезке и начнём уменьшать отрезок [t; ![]() ] приближая
] приближая ![]() t. Значение средней скорости будет стремиться к некоторому числу, т. е. к пределу, который называется мгновенной скоростью в момент времени t.
t. Значение средней скорости будет стремиться к некоторому числу, т. е. к пределу, который называется мгновенной скоростью в момент времени t. ![]() =
= ![]()
Наряду с И. Ньютоном основные законы математического анализа открыл немецкий математик Г.Лейбниц, решая задачу проведения касательной к произвольной кривой.
 Пусть дана некоторая кривая и точка P на ней. Возьмём на этой кривой другую точку
Пусть дана некоторая кривая и точка P на ней. Возьмём на этой кривой другую точку ![]() , и проведём прямую PР1, которую называют секущей.
, и проведём прямую PР1, которую называют секущей.
Заставим стремиться точку Р1 к точке Р по данной кривой. Тогда положение секущей будет меняться. Как только точка Р1 займёт положение точки Р, секущая займёт положение касательной к данной прямой в точке Р.
Т.о. предельное положение секущей при стремлении точки Р1 к точке Р будет касательная к кривой в точке Р.
Переведём описанное построение на язык формул.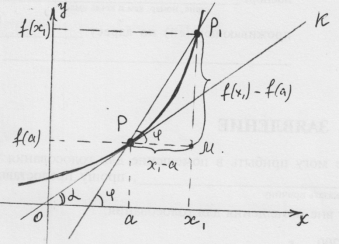 Пусть данная кривая является графиком некоторой функции y=f(x). Точка Р имеет координаты (а; f(а)). Точка Р1 имеет координаты (х1;f(x1)). РР1 — секущая. РК – касательная к графику функции в точке Р.
Пусть данная кривая является графиком некоторой функции y=f(x). Точка Р имеет координаты (а; f(а)). Точка Р1 имеет координаты (х1;f(x1)). РР1 — секущая. РК – касательная к графику функции в точке Р.
Угол φ– угол наклона секущей к положительному направлению оси ОХ.
Угол α — угол наклона касательной к положительному направлению оси ОХ.
И секущая, и касательная являются прямыми линиями, уравнение которых в общем виде записывается как у = kх + b, где k — угловой коэффициент к прямой равный тангенсу угла наклона прямой к положительному направлению оси ОХ. Из Δ РМР, имеем
k=tgφ=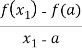
Т. к. касательная – это предельное положение секущей, то ![]() =tgα=
=tgα=![]() =
=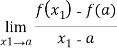
Итак, ![]() =
=![]() =
=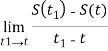 ;
;![]() =lim tgφ=
=lim tgφ=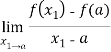
Мы видим, что две различные задачи привели в процессе решения к одному и тому же результату или, как чаще говорят в математике, к одной и той же математической модели — пределу разностного отношения функции и аргумента при условии, что разность аргументов стремится к нулю.
Решение многих задач сводится к необходимости осуществления предельного перехода в выражении вида 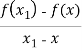 при стремлении
при стремлении ![]() к x. Этот предельный переход носит название дифференцирования функции, а сам предел отношения — производной функции.
к x. Этот предельный переход носит название дифференцирования функции, а сам предел отношения — производной функции.
Дифференцирование, или нахождение производной функции — это новая математическая операция, имеющая тот же смысл, что в механике нахождение скорости, в геометрии — вычисление углового коэффициента касательной.
Для нахождения значения производной в данной точке надо рассмотреть маленький участок изменения аргумента вблизи этой точки. Производная приближённо будет равна средней скорости на этом участке (на языке механики) или угловому коэффициенту секущей (на языке геометрии).
Для точного вычисления производной надо совершить предельный переход — стянуть отрезок изменения аргумента в точку. Тогда средняя скорость превратится в мгновенную, а секущая — в касательную, и мы вычислим производную.
Итак, при вычислении производной функции мы совершаем предельный переход. В чём его суть?
При определении функции мы имеем дело с переменными величинами. Пусть y = f(x) — функция от аргумента х. Рассмотрим, как ведёт себя функция f(x) при приближении х к некоторому числу a.
При х→а, f(x)→f(a). Иными словами ![]() =f(a).
=f(a).
Пусть заданы функции (¹) f(x)=3+![]() и f(x)=
и f(x)=![]() (²)
(²)
Предельный переход для (¹) и (²) функций при х→1 определим следующим образом:
![]() =
=![]() =3+
=3+![]() =4
=4
![]() =
=![]() =
=![]() =
=![]()
Если при х→![]() , f(x)→f(
, f(x)→f(![]() ) т. е.
) т. е. ![]() =f(
=f(![]() ), то говорят, что функция непрерывна в точке
), то говорят, что функция непрерывна в точке ![]() , а значит в этой точке она имеет производную. График этой функции плавная, непрерывная кривая линия.
, а значит в этой точке она имеет производную. График этой функции плавная, непрерывная кривая линия.
Определение производной функции.
Перейдём непосредственно к определению производной функции.
Пусть задана функция у = f(x). При сравнении значения этой функции в некоторой фиксированной точке ![]() со значениями функции в различных точках х, лежащих в окрестности
со значениями функции в различных точках х, лежащих в окрестности ![]() , удобно выражать разность f(x)-f(
, удобно выражать разность f(x)-f(![]() ) через разность х-
) через разность х-![]() .
.
Разность х-![]() называется приращением независимой переменной или приращением аргумента в точке х0 и обозначается Δх. Т.о. Δх=х-х0 (1). Из (1) следует, что х=х0+Δх (2).
называется приращением независимой переменной или приращением аргумента в точке х0 и обозначается Δх. Т.о. Δх=х-х0 (1). Из (1) следует, что х=х0+Δх (2).
Говорят также, что первоначальное значение аргумента х0 получило приращение Δх. Вследствие этого значение функции f тоже изменилось.
f(x)=f(x0+Δx), тогда Δf=f(x)-f(x0)=f(x0+Δx)-f(x0) (3)
Δf называется приращением функции в точке х0.
Из (³) следует, что f(x)=f(x0+Δx)=f(x0)+Δf (4)
Δf называют также приращением зависимой переменной и обозначают через Δу.
Механический смысл производной — скорость изменения функции в точке.
Геометрический смысл производной заключается в следующем: существование производной непрерывной функции в некоторой точке х0, равносильно существованию касательной, проведённой к графику данной функции в точке с абсциссой х0. Угловой коэффициент этой касательной равен тангенсу угла её наклона к положительному направлению оси ОХ и равно значению производной функции в точке х0.
k=tgα=f '(х0) (5)
Алгоритм нахождения производной
- Зафиксировав значение х, находим f(x).
- Придав аргументу х приращение Δх так, чтобы не выйти из области определения функции f(x), найти f(x+Δx).
- Вычислить приращение функции
Δf=f(x+Δx)-f(x)
-
Составить отношение
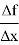
-
Найти предел отношения
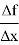 при Δх→0.
при Δх→0.
Теперь рассмотрим примеры нахождения некоторых функций на основе определения производной, применяя алгоритм ее нахождения.
Найти: 1) у=х, 2)у=Сх, 3)у=kx+b, 4)у=х2,у=![]() , 5)у=х3, 6)у=
, 5)у=х3, 6)у= ![]() ,7)у=хn, 8)у=
,7)у=хn, 8)у=![]() .
.
1. Найти у', если у=x.2. Найти у', если у=Сx.
1) х – фиксированное; f(x)=x 1) х – фиксированное; f(x)=Сx
2) Δx; x+Δx; f(x+Δx)=x+Δx2) Δx; x+Δx; f(x+Δx)=С(x+Δx)
3) Δf=f(x+Δx)-f(x)= 3)Δf=f(x+Δx)-f(x)=
=(x+Δx)-x=x+Δx-x= Δx =С(x+Δx)-Сx=Сx+СΔx-Сx= СΔx
4) ![]() =
=![]() =14)
=14) ![]() =
=![]() =С
=С
5)
Итак, x'=1.Итак, (Сx)'=С.
3. Найти у', если у=kx+b.4. Найти у', если у=х2
1) х – фиксированное;f(x)=kx+b1) х – фиксированное, f(x)=x2
2) Δx; x+Δx; f(x+Δx)=k(x+Δx)+b2) Δх; х+Δх; f(x+Δx)=(x+Δx)2
3)Δf=f(x+Δx)-f(x)=(k(x+Δx)+b)-(kx+b))=3) Δf=(x+Δx)2-x2= x2+2xΔx+(![]() )2-x2=
)2-x2=
=kx+kΔx+b- kx-b= kΔx=2xΔx+(![]() )2
)2
4) ![]() =
=![]() =k4)
=k4) ![]() =
=![]() =2x+Δx
=2x+Δx
5) ![]() =
=![]() =k5)
=k5) ![]() =
=![]() =2x
=2x
Итак, (kx+b)'=kИтак, (х2)'=2х.
5. Найти у', если у=х3 6. Найти у', если у=![]()
1) х – фиксированное, f(x)=x31) х – фиксированное, х≠0; f(x)=
2) Δх; х+Δх; f(x+Δx)=(x+Δx)32) Δх; х+Δх; f(x+Δx)=![]()
3) Δf=(x+Δx)3-x3= 3) Δf=![]() -
-![]() = -
= -![]()
=x3+3x2Δx+3x (![]() )2 +(
)2 +(![]() )3- x3= 4)
)3- x3= 4) ![]() = -
= -![]() = -
= - ![]()
=3x2Δx+3x (![]() )2 +(
)2 +(![]() )3 5)
)3 5) ![]() = -
= -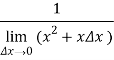 = -
= -![]()
Итак, (![]() )'= -
)'= - ![]()
4) ![]() =
=![]() =
=
=![]()
5) ![]() =
=![]() =
=![]()
Итак, (х3) '=![]() .
.
Зная производные у=х, у=х2,у=х3, можно методом частичной индукции записать производную для у=хn, т. е. (хn)'=![]()
![]() . Доказательство этой формулы можно и не приводить. В нашей работе обычно формула доказывается. Приведем ее.
. Доказательство этой формулы можно и не приводить. В нашей работе обычно формула доказывается. Приведем ее.
7. Найти у', если у=хn
1) х — фиксированное, f(x)=xn
2) Δх; х+Δх; f(x+Δx)=(x+Δx)n
Применим бином Ньютона для раскрытия скобок
(x + a)n = xn + ![]() axn-1 +
axn-1 + ![]() a2xn-2 +... +
a2xn-2 +... +![]() an-1xn + an,
an-1xn + an, ![]()
где k — порядковый номер слагаемого в многочлене, тогда
3) Δf=(x+Δx)n-xn= xn + ![]() Δxxn-1 +
Δxxn-1 + ![]() (Δx)2xn-2 — +... +
(Δx)2xn-2 — +... +![]() (Δx)n-1 xn + (Δx)n — - xn =
(Δx)n-1 xn + (Δx)n — - xn = ![]() Δx xn-1 +
Δx xn-1 + ![]() (Δx)2xn-2 +... +
(Δx)2xn-2 +... +![]() (Δx)n-1 xn + (Δx)n
(Δx)n-1 xn + (Δx)n
4) ![]() =
=![]()
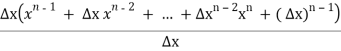 =
=
= ![]()
5) ![]() =
=![]() =
=![]() , где
, где ![]() =
=![]()
Итак, (хn)'=
8. Найти у', если у=![]()
Преобразуем ![]() =
=![]() . Так как, (хn)'=
. Так как, (хn)'=![]() , тогда
, тогда ![]() ) '=
) '=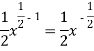 =
=![]() .
.
Следовательно, ![]() ) '=
) '=![]() .
.
С помощью приведённого алгоритма выводятся все формулы и правила дифференцирования. Таким образом, заполняется таблица производных. Самое главное все формулы выводятся, а не даются в готовом виде.
Литература:
- Рогановский Н. М. Методика преподавания в средней школе. Мн., «Высшая школа», 1990.
- Фройденталь Г. Математика как педагогическая задача. М., «Просвещение», 1998.
- Н.Н. Математическая лаборатория. М., «Просвещение», 1997.
- Колягин Ю. М. Методика преподавания математики в средней школе. М., «Просвещение», 1999.
- Столяр А. А. Логические проблемы преподавания математики. Мн., «Высшая школа», 2000.
- Далингер В. А. Начала математического анализа. — Омск: ООО «Издательство Полиграфист», 2002. – 158 с.







