Введение
Анализ временных рядов представляет собой одну из наиболее важных областей в экономической теории и практике. Характерной особенностью временных рядов является то, что наблюдения за некоторым объектом производятся последовательно во времени (например, ежедневный объем продаж какого-нибудь товара, уровень инфляции, обменный курс валют) — все это временные ряды.
Целью данной работы является проверка возможности изучения временных финансовых рядов методами, развитыми в последнее время с тем чтобы в дальнейшем применять эти методы в экономических и финансовых исследованиях. Мы ограничимся методами спектрального анализа рядов, в котором целью анализа является разложение комплексные временные ряды с циклическими компонентами на несколько основных синусоидальных функций с определенной длиной волн. Базовая идея анализа временного ряда по Фурье состоит в том, чтобы разделить данные на сумму синусоид с различными длинами циклов.
Наиболее известный пример применения спектрального анализа — циклическая природа солнечных пятен. Оказывается, что активность солнечных пятен имеет 11-ти летний цикл. Другие примеры небесных явлений, изменения погоды, колебания в товарных ценах, экономическая активность и т. д. также часто используются в литературе для демонстрации этого метода. цель спектрального анализа — распознать сезонные колебания различной длины.
Основными недостатками традиционного анализа Фурье можно назвать следующие.
1. Недостаточная информативность при анализе нестационарных сигналов и практически полное отсутствие возможностей анализа их особенностей (сингулярностей). Появляются «паразитные» высокочастотные составляющие, явно отсутствующие в исходном сигнале при наличии в нём скачков и разрывов.
2. Гармонические базисные функции разложения не способны в принципе отображать перепады сигналов с бесконечной крутизной типа прямоугольных импульсов, так как для этого требуется бесконечно большое число членов ряда. При конечном числе членов ряда Фурье в окрестностях скачков, разрывов и т. п. в восстановленном сигнале возникают значительные осцилляции − явление Гиббса (Gibbs phenomenon).
3. Преобразование Фурье отображает общие сведения о частотах исследуемого сигнала в целом и не дает представления о локальных свойствах сигнала при быстрых временных изменениях его спектрального состава. Классический алгоритм преобразования Фурье в принципе не предоставляет возможности анализировать частотные характеристики сигнала в произвольные моменты времени. Напомним, что, используя преобразование Фурье, можно работать с сигналом либо только во временной области, либо только в частотной. Для стационарного сигнала эта информация и не требуется, поскольку частотные составляющие сигнала и их амплитуды на любом временном интервале идентичны.
Кроме этого существует фундаментальная проблема, связанная с конечностью исследуемого ряда, в то время как преобразование Фурье требует, чтобы функция была заданной и периодичной на бесконечном интервале.
Преодолеть эти ограничения удалось с развитием в 80-х годах XX века метода вейвлет-анализа. Само слово «wavelet» буквально означает «маленькая волна», или «всплеск» − термин, использовавшийся одно время в отечественной литературе Вейвлет-анализ стали широко применять в классических областях, таких как анализ и обработка числовых рядов физических, геофизических и тому подобных результатов экспериментов и наблюдений. Теперь он широко используется при распознавании синтезе сигналов различной природы и структур (например, речи), при анализе кардиограмм, при диагностике острых лейкозов, также для решения задач обработки, сжатия, хранения и передачи больших объёмов информации, в том числе аналогового и цифрового изображения (JPEG-2000) и видео (MPEG-4).
Многие исследователи называют вейвлет-анализ своеобразным «математическим микроскопом» для точного изучения внутреннего состава и структур неоднородных сигналов и функций.
Наглядно различия между классическим фурье-преобразованием, оконным фурье-преобразованием и вейвлет-преобразованием демонстрирует рис. 1.
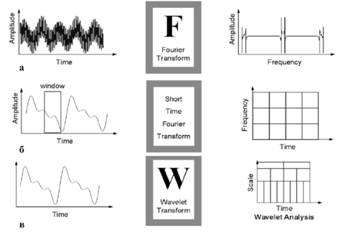
Рис. 1. Схематическое изображение исследования сигнала преобразованием Фурье (а), оконным фурье-преобразованием (б) и вейвлет-преобразованием (в). Фурье-преобразование показывает амплитудно-частотную характеристику сигнала — наличие и амплитуду различных гармоник в сигнале. Оконное фурье-преобразование демонстрирует наличие гармоник в сигнале в заданном диапазоне движущегося вдоль временной оси окна. Вейвлет-преобразование демонстрирует масштабные сравнения сигнала с заданными базовыми вейвлетами в каждый момент времени существования сигнала
В классическом фурье-анализе естественным образом в качестве базовых функций используются синусы и косинусы или в общем виде — комплексная экспонента. Были попытки использования других ортогональных функций (например, ортогональных полиномы), но они оказались сложными в интерпретации результатов.
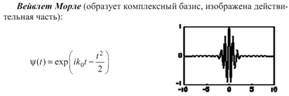
В вейвлет-анализе выбор базовых функций огромен и постоянно расширяется. На рис. 2 приведены самые популярные основные классические вейвлеты, с которых «всё начиналось», и применение которых в настоящее время наиболее упрощено благодаря включению вейвлет-преобразований в виде стандартных приложений в математические пакеты.
|
|
|
|
|
|
|
|
Рис. 2.
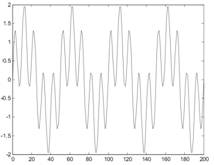
Приведем пример Фурье-анализа двух сигналов стационарного и нестационарного. Первый сигнал, представляющий собой сумму двух синусоид с частотой 10 и 50 Гц, представлен на рис. 3а
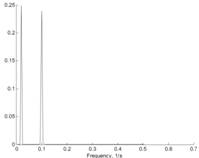
а) б)
Рис. 3а Стационарный сигнал, представляющий собой сумму двух синусоид с частотой 10 и 50 Гц и его спектральная характеристика 3б)
Этот сигнал стационарен в том смысле, что частоты, в нем содержащиеся, не меняются во времени. На его спектральной характеристике, как и следовало ожидать, видны два пика, в идеале представляющие собой δ-функции.
Теперь для сравнения рассмотрим нестационарный сигнал. Для простоты рассмотрим сигнал, в котором присутствуют те же самые частоты, что и в упомянутом примере, но эти частоты встречаются на различных временных интервалах (рис. 4а). Рассмотрим спектр этого нестационарного сигнала (рис. 4б). На рисунке чётко видны две частоты. «Ложные частоты» имеют небольшую амплитуду, и они появляются из-за наличия скачка значения функции и её производной в момент смены частоты. Не считая этих частот, как и на рис. 3а, видны две основные гармоники, присутствующие в исходном сигнале.
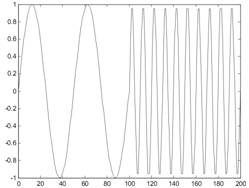
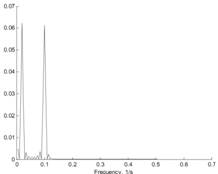
а) б)
Рис. 4а. Нестационарный сигнал, содержащий синусоиды 10 Гц и 50 Гц на различных временных интервалах и его спектральная характеристика 4б)
Таким образом, отличия в спектральных характеристиках рассмотренных двух сигналов незначительны: присутствуют ложные частоты малых амплитуд в нестационарном сигнале (рис. 3б и 4б).
Рассмотренный пример показывает, что по своей сути преобразование Фурье дает представление о том, какие частоты в спектре сигнала присутствуют, но не может ответить на вопрос, каково время существования спектральных составляющих сигнала. Для временной локализации спектральных компонентов необходимо сконструировать частотно-временное представление сигнала. Эту задачу в некоторой степени может решить так называемое оконное преобразование Фурье, однако наиболее полно её решает вейвлет-преобразование.
Приведём для сравнения вейвлет-преобразование обсуждаемого ранее примера с двумя гармониками. ВП суммы двух гармоник (10 и 50 Гц) и тех же гармоник, действующих на двух последователь-ных интервалах, изображены на рис. 5а), 5б).
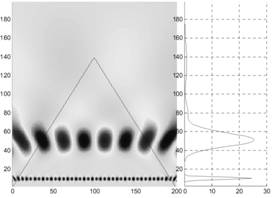
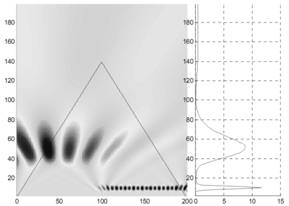
а) б)
Рис. 5а. Вейвлет-преобразование стационарного сигнала, состоящего из набора двух гармоник
Рис. 5б. Вейвлет-преобразование нестационарного сигнала, состоящего из последовательного включения двух гармоник
Вейвлет-анализ финансовых рядов
Мы применили описанный метод использовали временные ряды динамики изменения мировых валют по отношению к рублю.
На рис.6 изображены графики курса евро (6а) и доллара США (6б) за 2007–2013 года, представленные на сайте www.alta.ru компанией АЛЬТА-СОФТ.
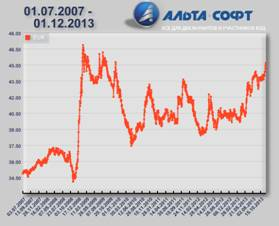
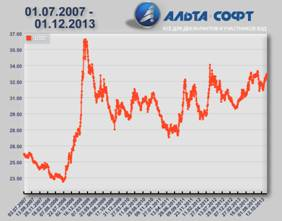
а) б)
Рис. 6.
Рис. 7.а) и 7.б) демонстрирует вейвлет-спектры каждого из рядов. На графике с)Power отчетливо видно, что основной максимум энергии в спектре приходится на диапазон масштабов времени 3–4 года, то есть основным в эволюции в данную эпоху является тренд вокруг кризиса 2008 года.
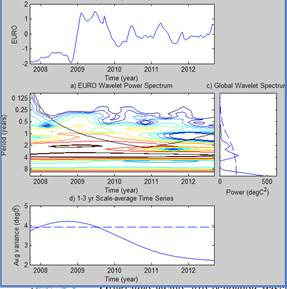
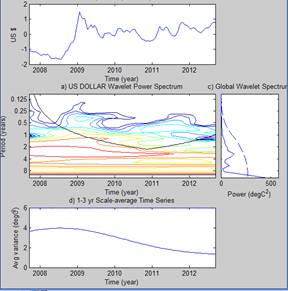
а) б)
Рис. 7.
Следующий этап нашего исследования — вычисление кросс-вейвлет спектра обоих исследуемых рядов. Для этого мы использовали программу WTC-16, разработанную для пакета MATLAB 7.0. Кросс-вейвлет спектр представляет собой свертку комплекснозначных и взаимно-сопряженных вейвлет-спектров каждого из рядов. И показывает наибольшие значения на тех временах и масштабах, где оба ряда ведут себя подобным друг другу образом.
Результаты вычислений представлены на рис. 8.
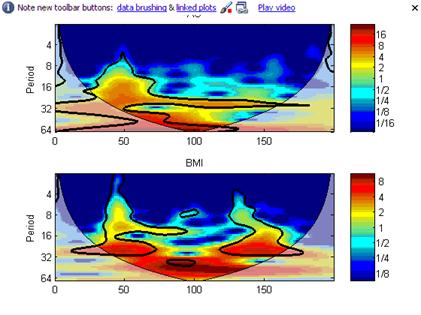
Рис 8 а). Вейвлет-спектры рядов, представленных на рис. 6а. и 6б.
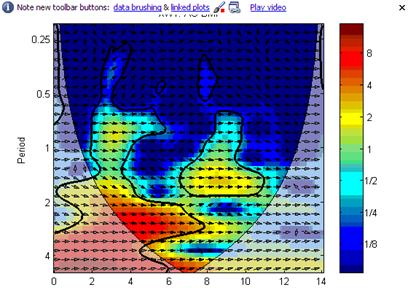
Рис. 8.б) Взаимный кросс-вейвлет спектр рядов 6.а, 6.б.
Наибольшая корреляция рядов наблюдается в период кризиса конца 2008 года (красный цвет на диаграмме). Стрелки право означают небольшое опережение ряда US $ перед рядом EURO.
Заключение. Возможность одновременно при сопоставлении рядов изучать и пространственную и частотную картину их эволюции, а также проводить совместный кросс-анализ на диаграмме является очень важным достоинством описанного метода. Особенно интересно рассмотреть такие ряды для разных финансовых индексов и в различные эпохи экономического развития. Мы предполагаем получить эти результаты в дальнейшем.
Литература:
1. Нагорнов, О. В. Вейвлет-анализ в примерах, М.: НИЯУ МИФИ, 2010. — 120 с.
2. Астафьева Н. М. Вейвлет-анализ: Основы теории и примеры применения // Успехи физических наук, 1996, т.166, № 11.
3. Воробьев В. И., Грибунин В. Г. Теория и практика вейвлет-преобразования // ВУС, 1999. С.1–204.
4. Дьяконов В., Абраменкова И. MATLAB. Обработка сигналов и изображений. Специальный справочник. СПб.: Питер, 2002.