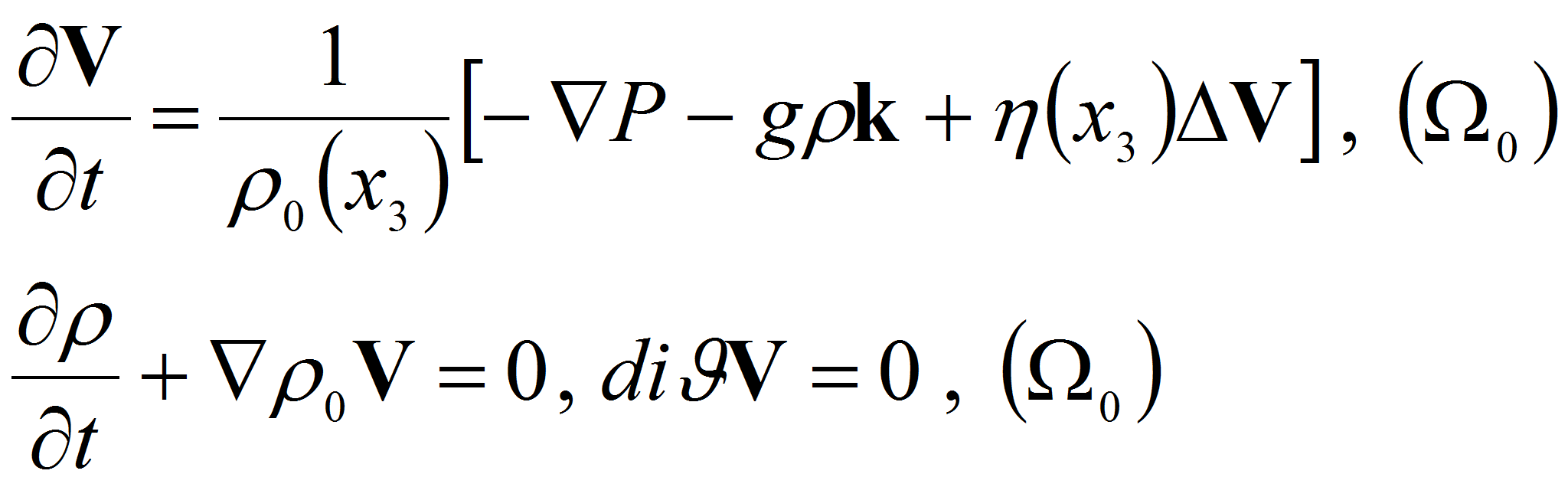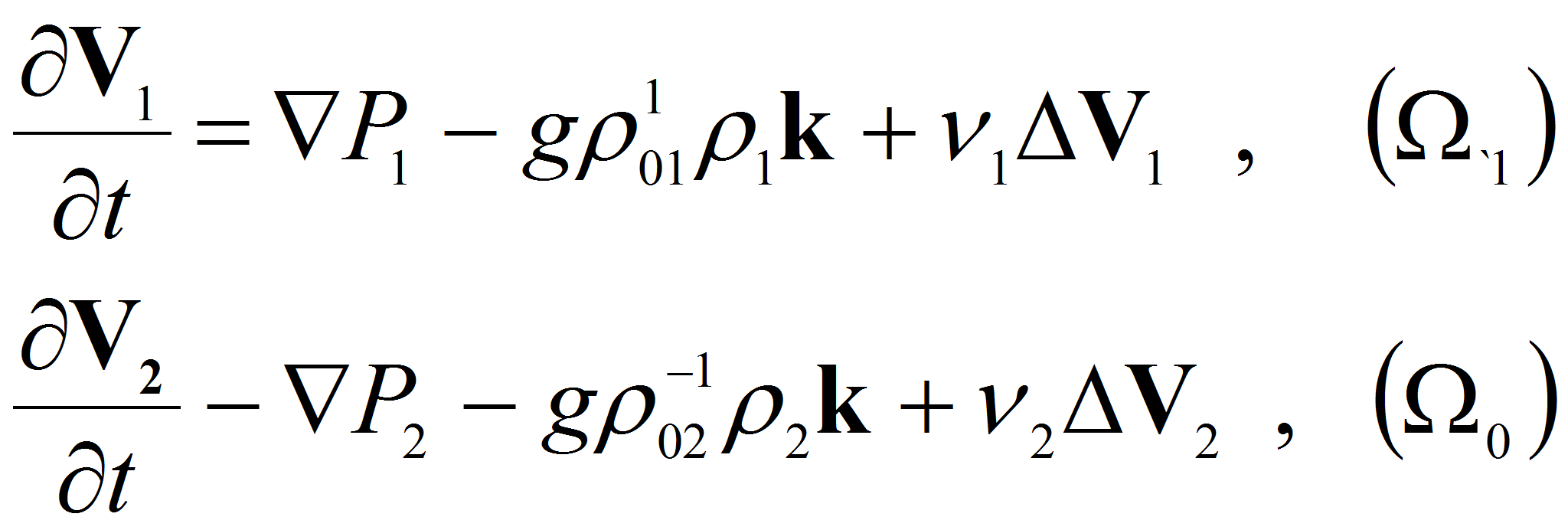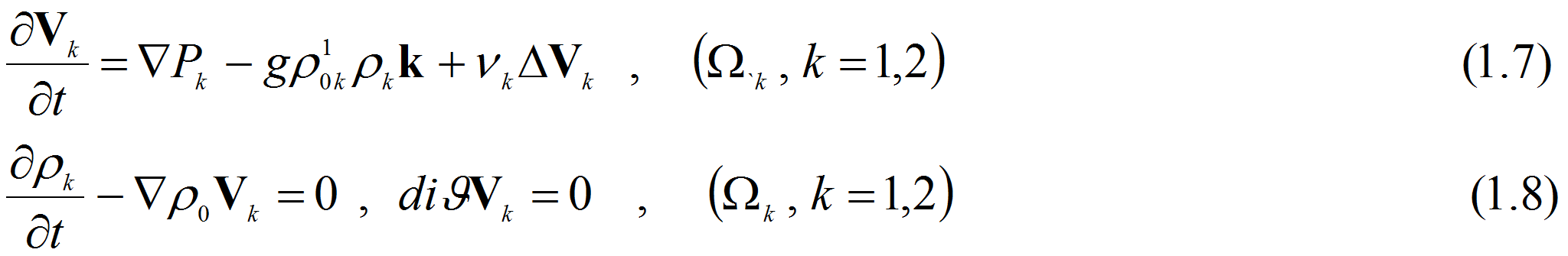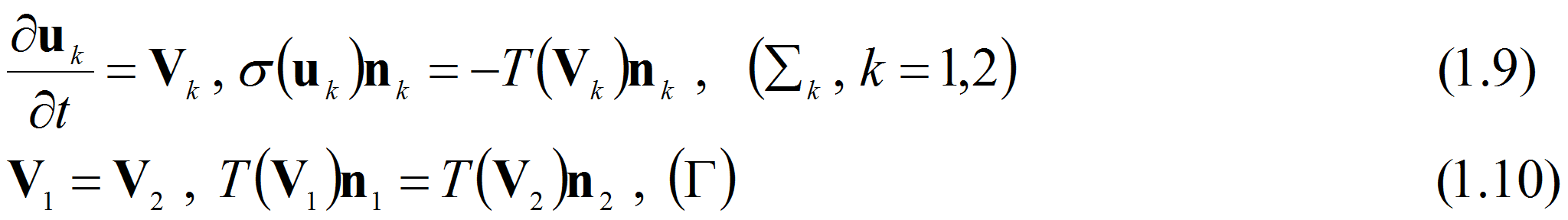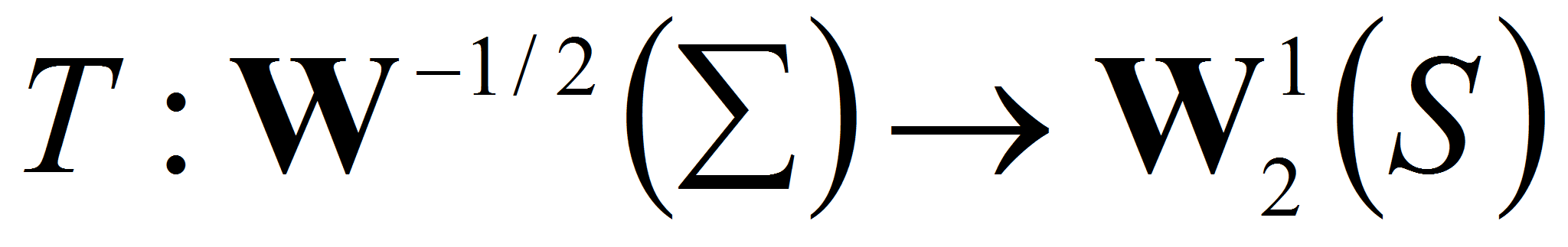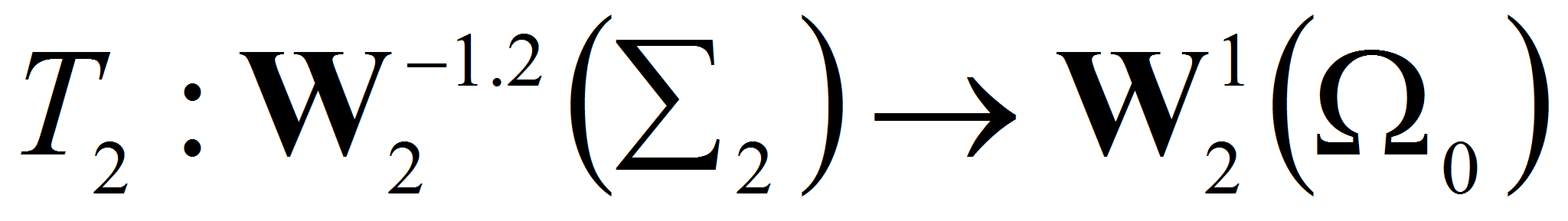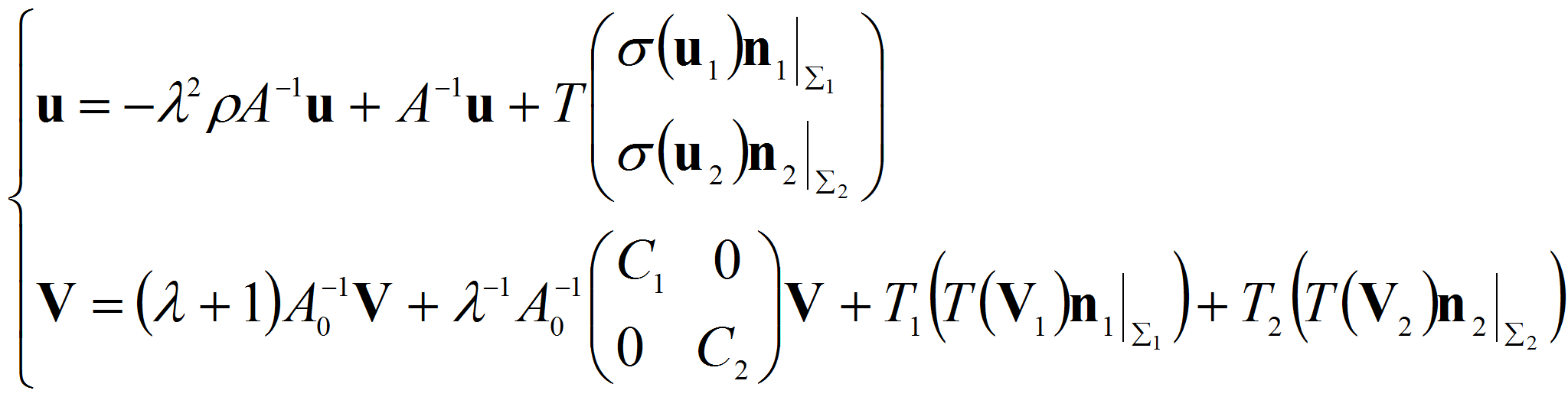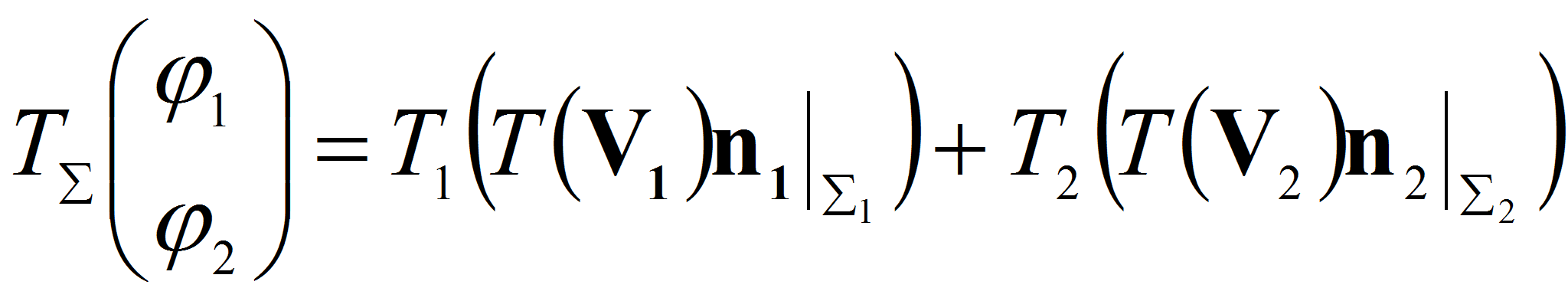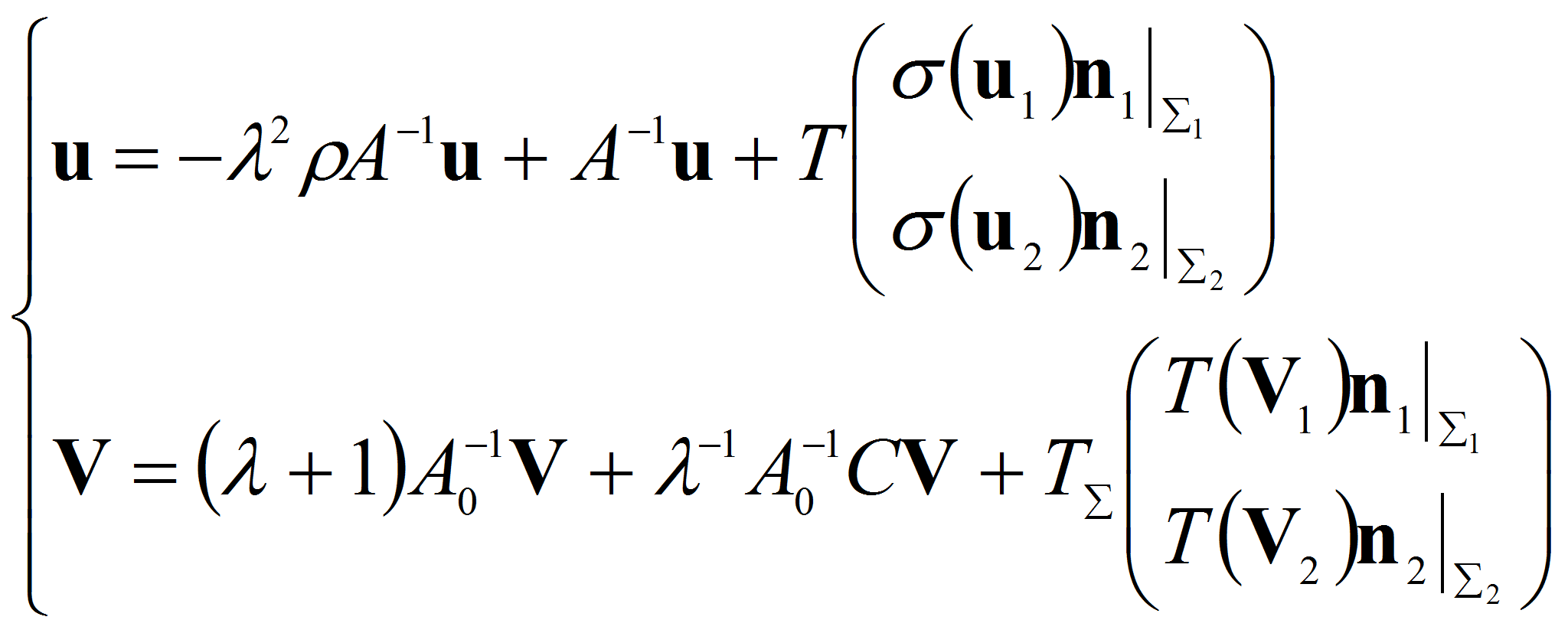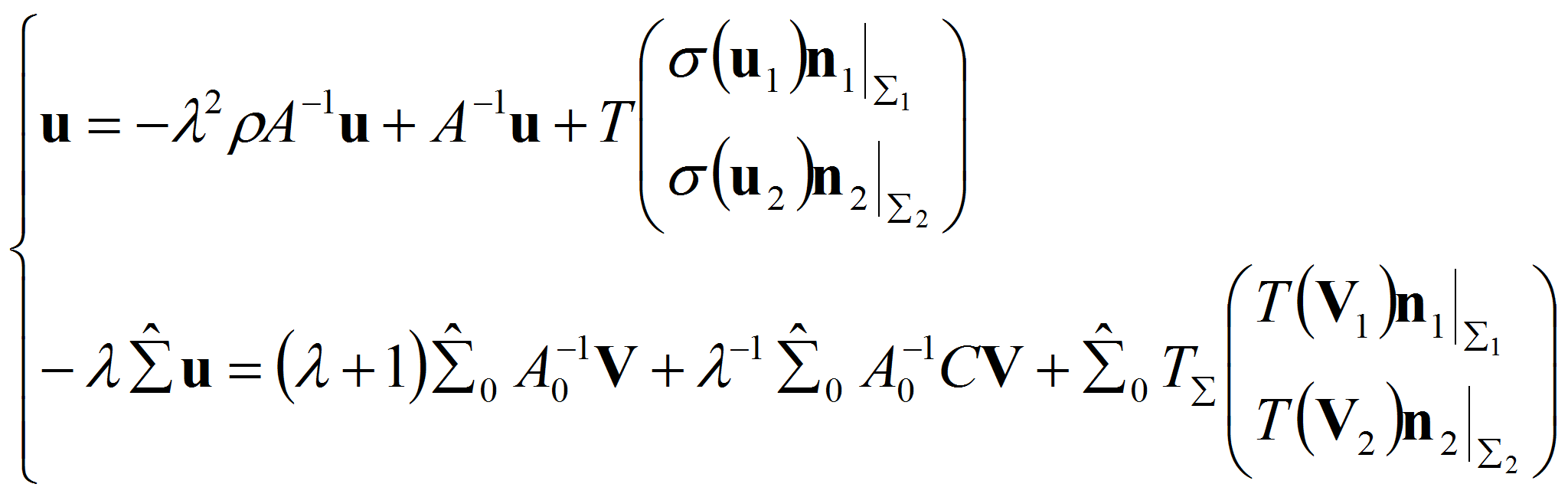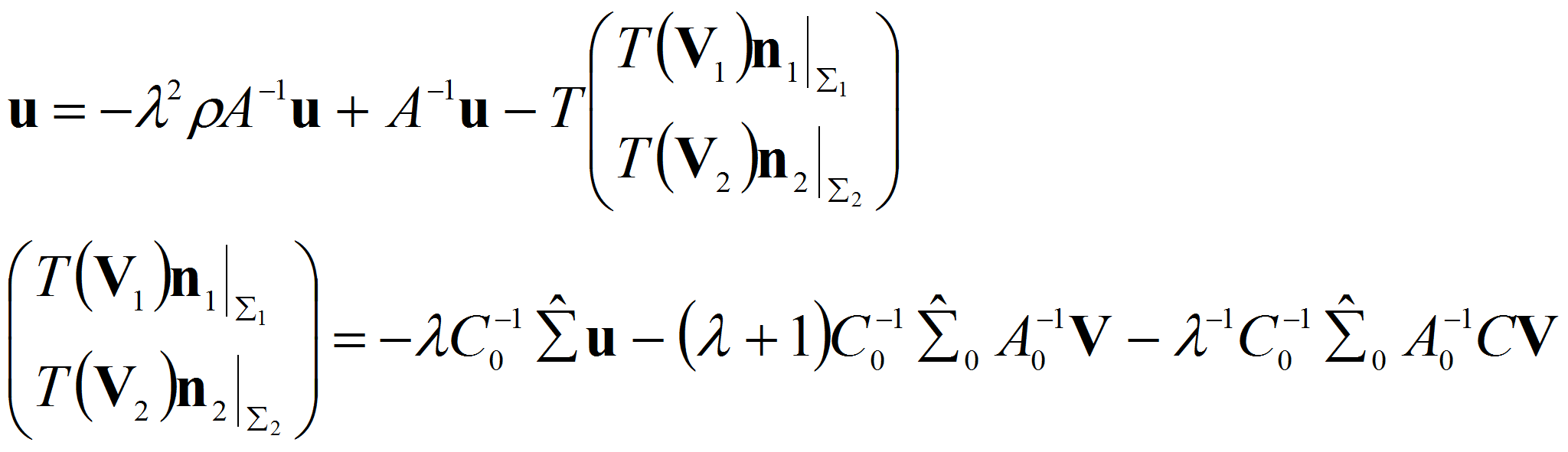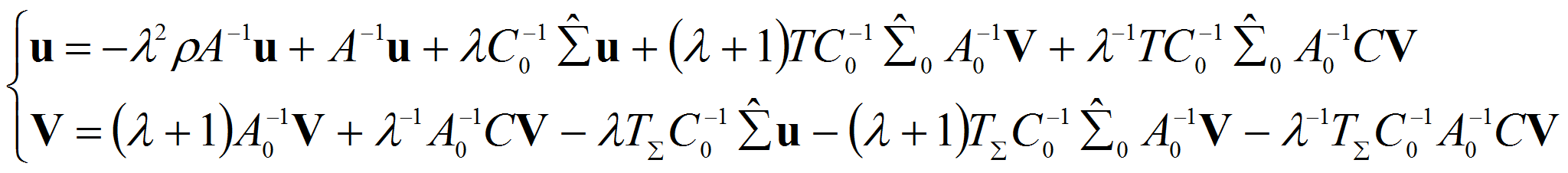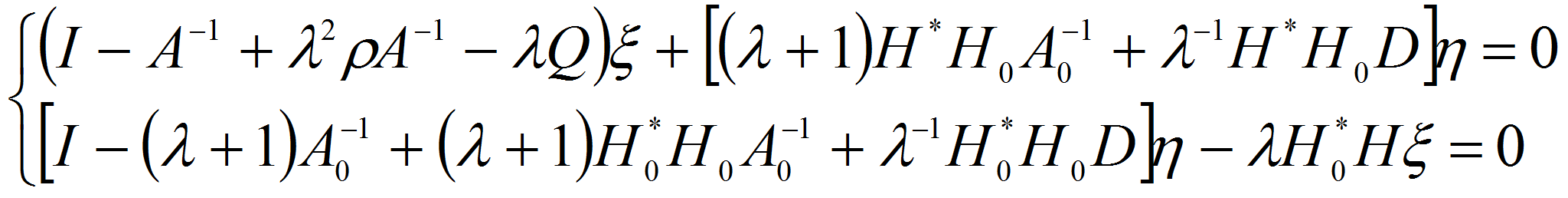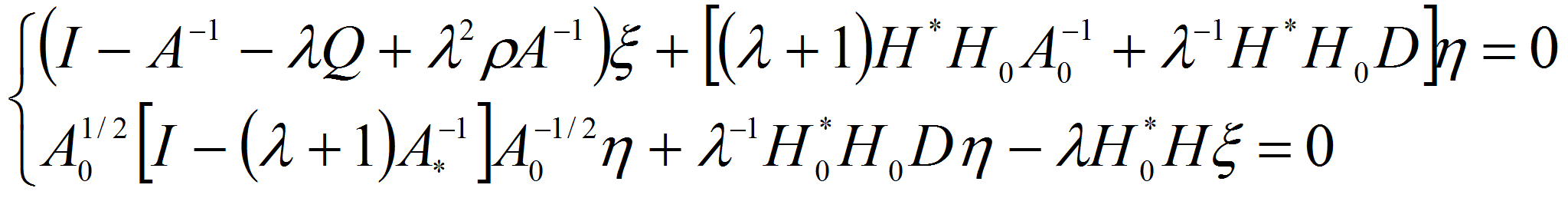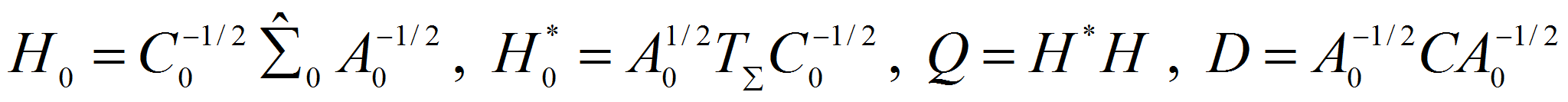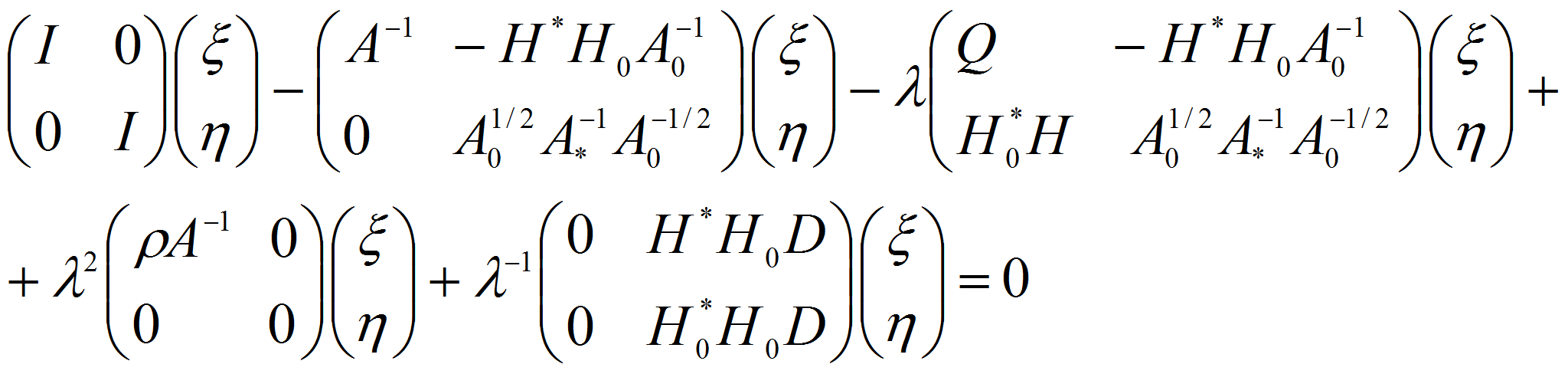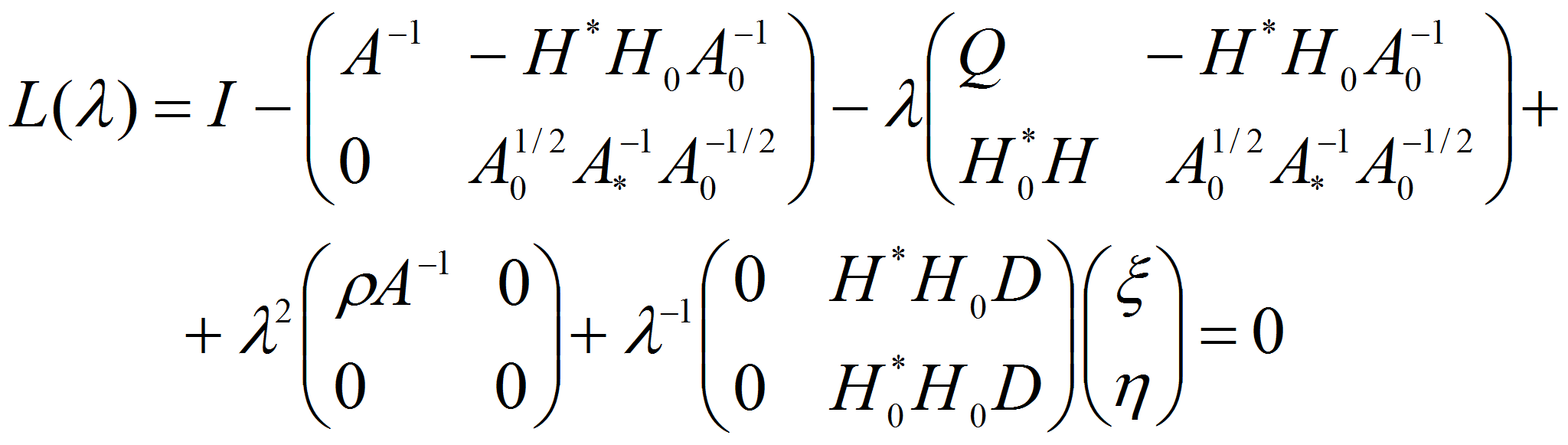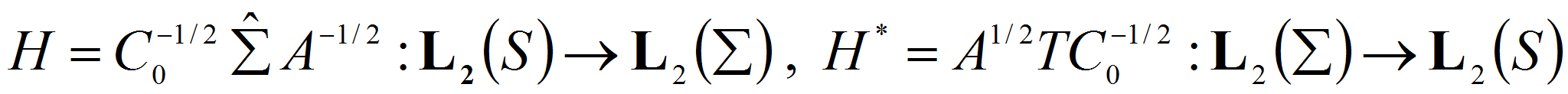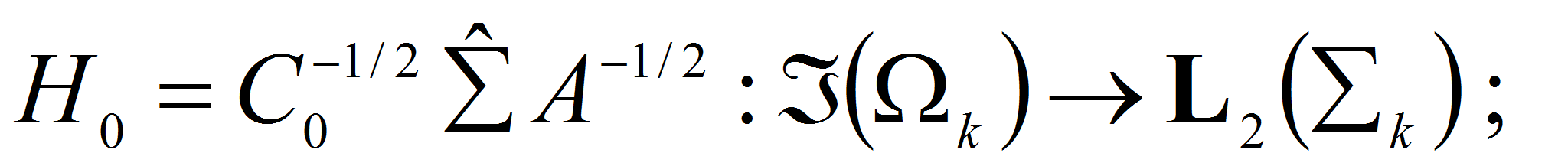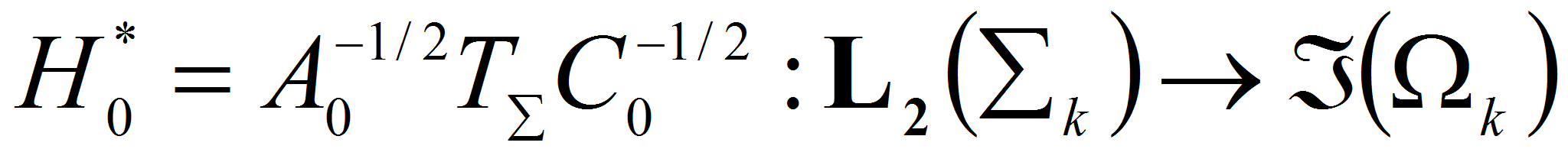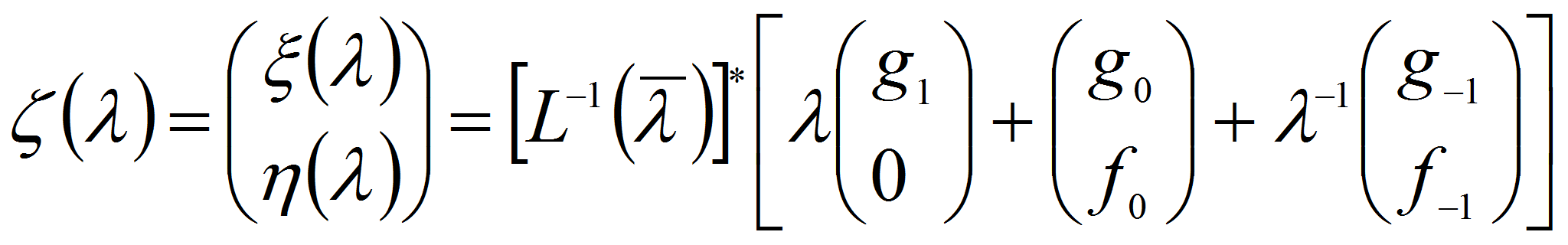Изучаются свойства собственных значений и собственных функций в задаче о нормальных колебаниях вязкой несжимаемой стратифицированной жидкости, заполняющей упругий сосуд. Получены утверждения о локализации спектра и доказана терема о полноте собственных функций с конечным дефектом.
Изучение задач о движении жидкости в сосуде
относятся к числу классических задач гидромеханики. Движения жидкости
и сосуда, зависящие от времени как
![]() называются нормальными или свободными.
называются нормальными или свободными.
Задачи о колебаниях вязкой стратифицированной жидкости в неподвижном
сосуде рассматривались в
![]() .
В
.
В
![]() были исследованы некоторые задачи о колебаниях вязкой несжимаемой
однородной жидкости в упругом сосуде, однако условия согласования
между жидкостью и упругим сосудом в этой работе носили математической
характер.
были исследованы некоторые задачи о колебаниях вязкой несжимаемой
однородной жидкости в упругом сосуде, однако условия согласования
между жидкостью и упругим сосудом в этой работе носили математической
характер.
Настоящая работа посвящена задаче о нормальных колебаниях системы
вязких несжимаемых стратифицированных жидкостей в упругом сосуде. При
этом условия согласование между упругой стенкой и жидкостью будет
выписано, как это принято в линейной теории. Часть результатов данной
работы изложена в
![]() .
.
1. Постановка задачи. Рассмотрим ограниченную
область
![]() и
пусть
и
пусть
![]() подобласть и
подобласть и
![]() ,
причем границы
,
причем границы
![]() класса
класса
![]() .
.
Пусть в упругом сосуде занимающем область
![]() находится система из двух вязких стратифицированных несжимаемых
жидкостей заполняющая область
находится система из двух вязких стратифицированных несжимаемых
жидкостей заполняющая область
![]() .
Границы раздела жидкостей обозначим через
.
Границы раздела жидкостей обозначим через
![]() .
Пусть
.
Пусть
![]() и
и
![]() части
части
![]() ,
лежащие соответственно ниже и выше
,
лежащие соответственно ниже и выше
![]() .
.
![]()
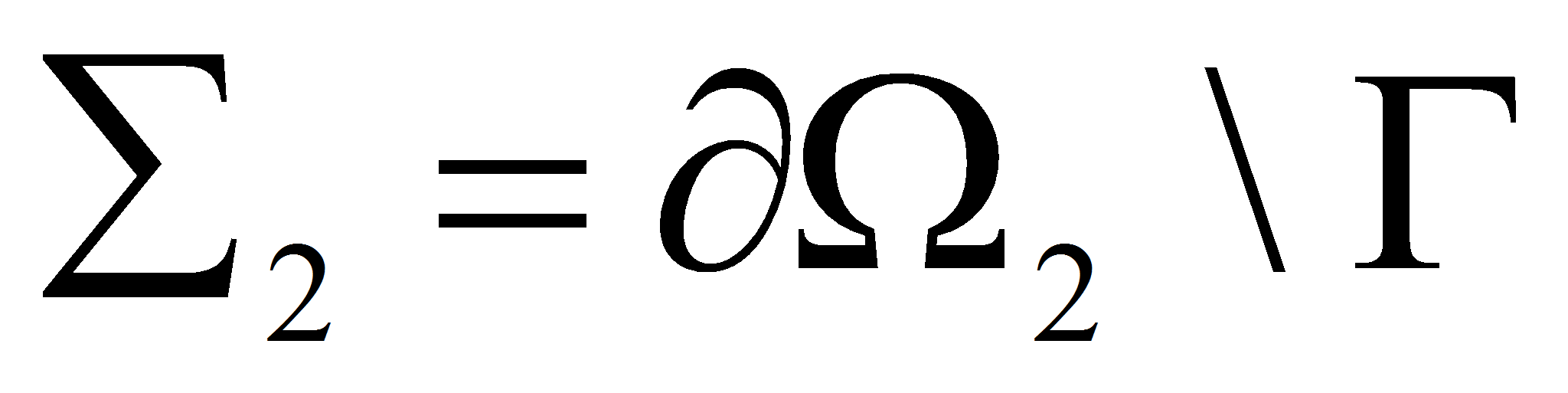 .
Соответствующий участок упругого сосуда обозначим через
.
Соответствующий участок упругого сосуда обозначим через
![]() Напомним, что основным частотным параметром, характеризующий
распространение и типы волн в стратифицированной жидкости, является
так называемая частота Вяйсяля – Брента
Напомним, что основным частотным параметром, характеризующий
распространение и типы волн в стратифицированной жидкости, является
так называемая частота Вяйсяля – Брента
![]() которая определяется соотношением
которая определяется соотношением
где
![]() и
и
![]() соответственно стационарное распределение плотности и его
производная, а
соответственно стационарное распределение плотности и его
производная, а
![]() ускорение
свободного падения. Будем считать, что на стратифицированную жидкость
действует гравитационное поле с ускорением
ускорение
свободного падения. Будем считать, что на стратифицированную жидкость
действует гравитационное поле с ускорением
![]() оси
оси
![]() декартовой системы координат
декартовой системы координат
![]() .
Рассматривается случай устойчивой стратификации жидкости:
.
Рассматривается случай устойчивой стратификации жидкости:
где
![]() считается непрерывной функцией
считается непрерывной функцией
![]() Тогда в приближении Буссинеска линеаризованные уравнения движения
стратифицированной вязкой жидкости в объеме
Тогда в приближении Буссинеска линеаризованные уравнения движения
стратифицированной вязкой жидкости в объеме
![]() примут вид
примут вид
![]()
где
![]() динамическая
вязкость,
динамическая
вязкость,
![]() отклонение
плотности от положения равновесия
отклонение
плотности от положения равновесия
![]() скорость
частицы жидкости. Чтобы упростить первое уравнение из (1.3) в области
скорость
частицы жидкости. Чтобы упростить первое уравнение из (1.3) в области
![]() заменим его приближенными уравнениями в областях
заменим его приближенными уравнениями в областях
![]() и
и
![]()
где
![]() константы,
усредняющие в областях
константы,
усредняющие в областях
![]() и
и
![]() значений
значений
![]() усредняют значения
усредняют значения
![]()
![]() отклонения
плотности от положения равновесия в областях
отклонения
плотности от положения равновесия в областях
![]() и
и
![]() .
При этом на границе соприкосновения
.
При этом на границе соприкосновения
![]() должны, очевидно, выполнятся условия
должны, очевидно, выполнятся условия
где первое равенство означает непрерывность скорости, а второе – равенство напряжений. Здесь
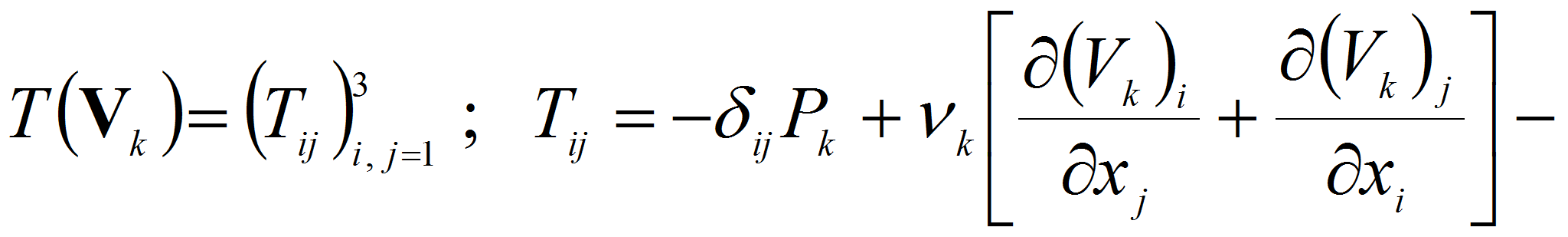 тензор
Навье – Стокса, соответствующий течению
тензор
Навье – Стокса, соответствующий течению
![]() внешняя
нормаль на Г к
внешняя
нормаль на Г к
![]() .
.
Если теперь область
![]() заполнена вязкой стратифицированной жидкостью, уравнения движения
которой мы описываем приближенной системой (1.4) , (1.5) то уравнения
свободных колебаний такой механической системы примут вид:
заполнена вязкой стратифицированной жидкостью, уравнения движения
которой мы описываем приближенной системой (1.4) , (1.5) то уравнения
свободных колебаний такой механической системы примут вид:
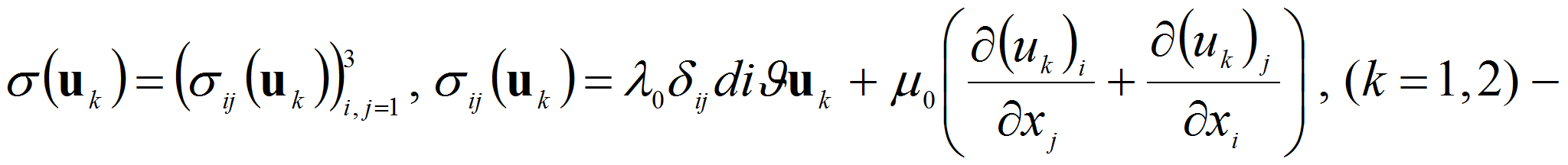 тензор
напряжений изотропного упругого тела,
тензор
напряжений изотропного упругого тела,
![]() постоянные
Ляме,
постоянные
Ляме,
![]() символ
Кронекера,
символ
Кронекера,
![]() плотность
тела, нормаль
плотность
тела, нормаль
![]() внешняя
к той области, из которой берется нормальная производная. Краевое
условие (1.6) означает отсутствие напряжений на
внешняя
к той области, из которой берется нормальная производная. Краевое
условие (1.6) означает отсутствие напряжений на
![]() Первое равенство (1.9) является условием прилипания вязкой жидкости
на стенке
Первое равенство (1.9) является условием прилипания вязкой жидкости
на стенке
![]() а второе равенство напряжений на
а второе равенство напряжений на
![]() .
(1.11) начальные данные.
.
(1.11) начальные данные.
Чтобы получить задачу на собственные значения будем искать решения,
зависящие от времени как
![]() Подставляя решение такого вида в (1.6) – (1.10) и с помощью
возникающих равенств
Подставляя решение такого вида в (1.6) – (1.10) и с помощью
возникающих равенств
исключая плотности
![]() ,
придем к системе
,
придем к системе
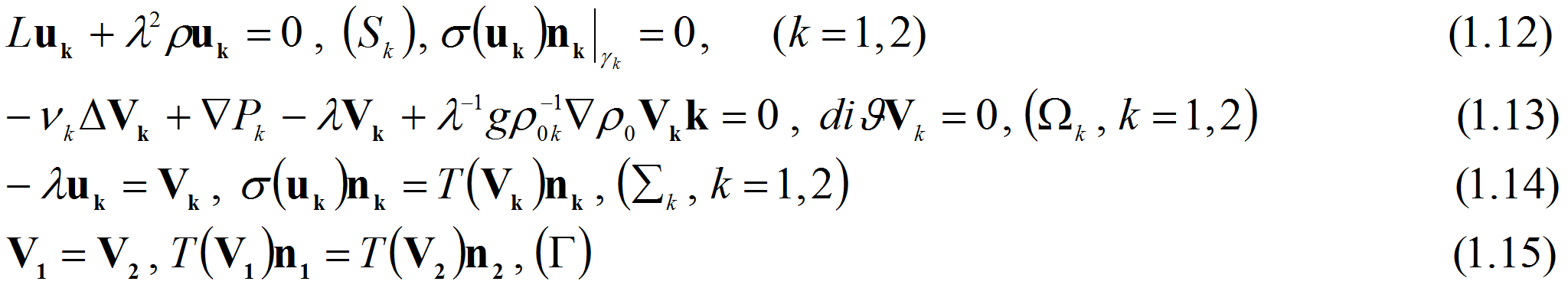 Именно
эта система является объектом исследования последующих пунктов и цель
которую мы ставим, состоит в том чтобы изучить структуру спектра и
свойства собственных функций указанной задачи.
Именно
эта система является объектом исследования последующих пунктов и цель
которую мы ставим, состоит в том чтобы изучить структуру спектра и
свойства собственных функций указанной задачи.
- 2. Переход к операторному уравнению. Положим
и обозначим
![]() подпространство в
подпространство в
![]() .
.
Для дальнейшего исследования задачу (1.12) – (1.15) сведем к операторному пучку. С этой целью рассмотрим следующие вспомогательные задачи:
Задача I. По функции
![]() найти решение задачи
найти решение задачи
Задача II.
По функции
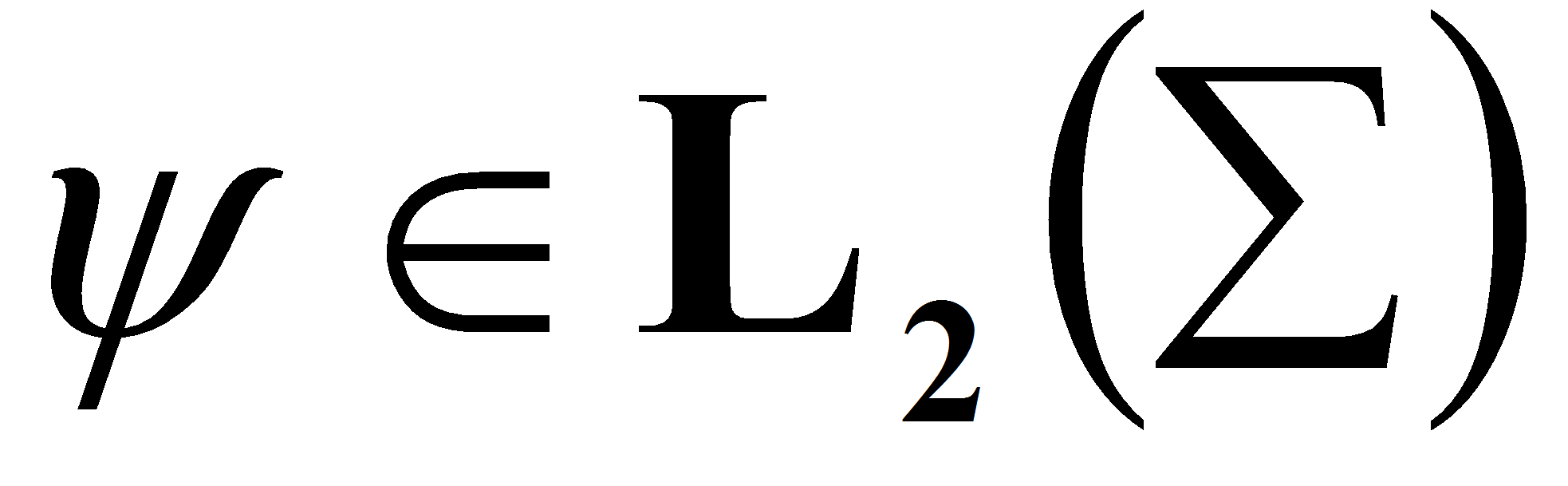 найти
решение задачи
найти
решение задачи
Из результатов работ
![]() и
и
![]() следует каждой из этих задач отвечает оператор, которой однозначно
задает обобщенное решение задачи. Выпишем последовательно обозначения
для этих операторов и перечислим их свойства.
следует каждой из этих задач отвечает оператор, которой однозначно
задает обобщенное решение задачи. Выпишем последовательно обозначения
для этих операторов и перечислим их свойства.
I. В задаче I
возникает компактный оператор
![]() причем
причем
II. В задаче II возникает непрерывный оператор
III. В задаче III возникает компактный, самосопряженный оператор
IV. В задаче IV (а) возникает непрерывный оператор
В задаче IV (б) возникает непрерывный оператор
Заметим теперь, что если
![]() решение задачи, отвечающее числу
решение задачи, отвечающее числу
![]() ,
то с помощью введенных операторов задача (1.12-1.15) может быть
записана в виде системы:
,
то с помощью введенных операторов задача (1.12-1.15) может быть
записана в виде системы:
Введем операторы
Тогда последнюю систему можно записать в виде
Учитывая, что в силу (1.14)
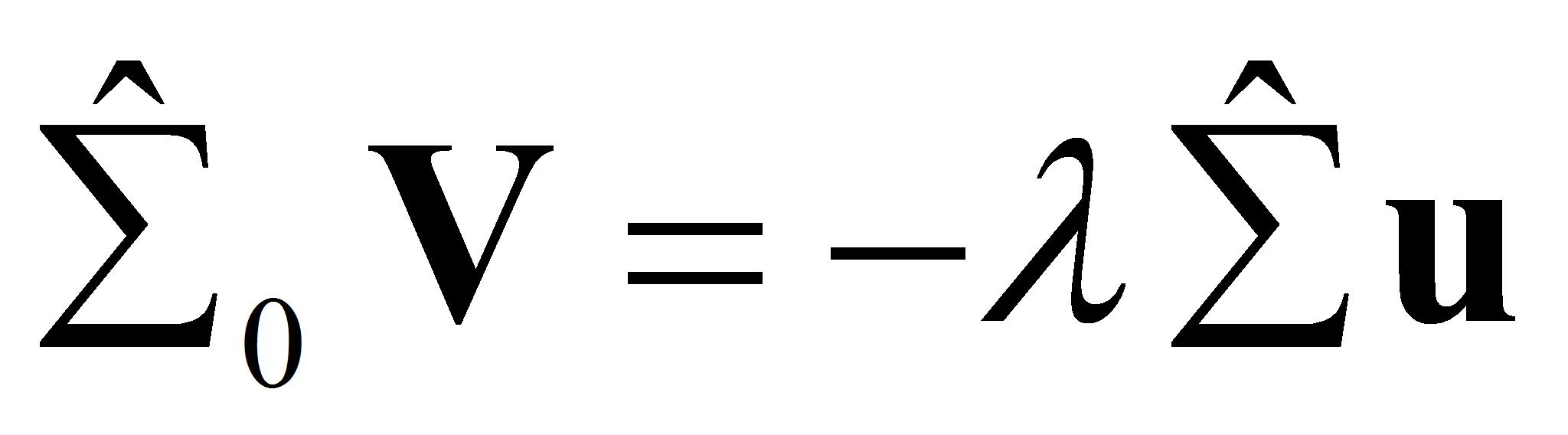 и применяя к второму равенству системы (2.1) оператор взятия следа
и применяя к второму равенству системы (2.1) оператор взятия следа
![]() получим
получим
где
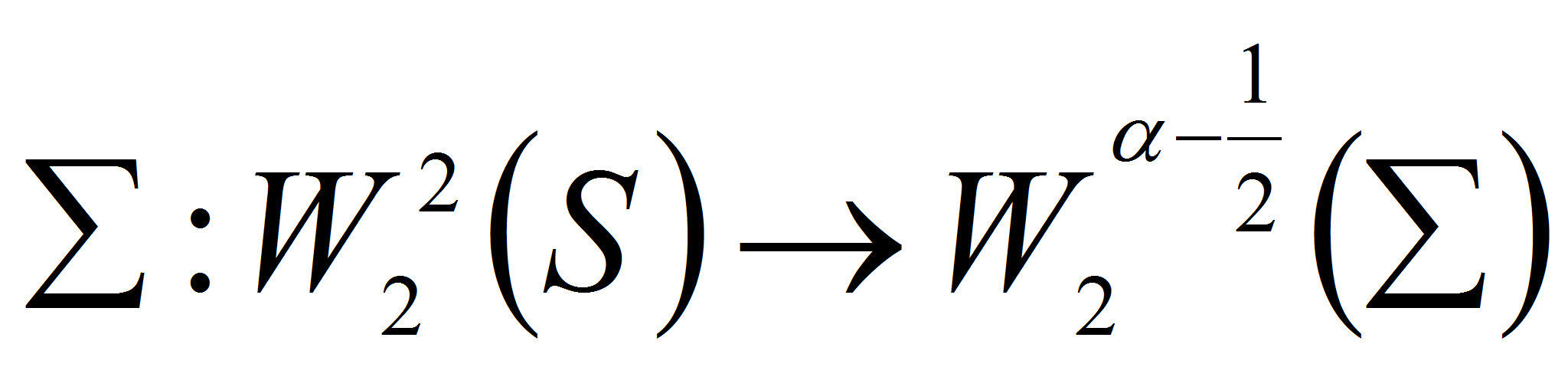 оператор взятия следа
оператор взятия следа
![]() Введем обозначение
Введем обозначение
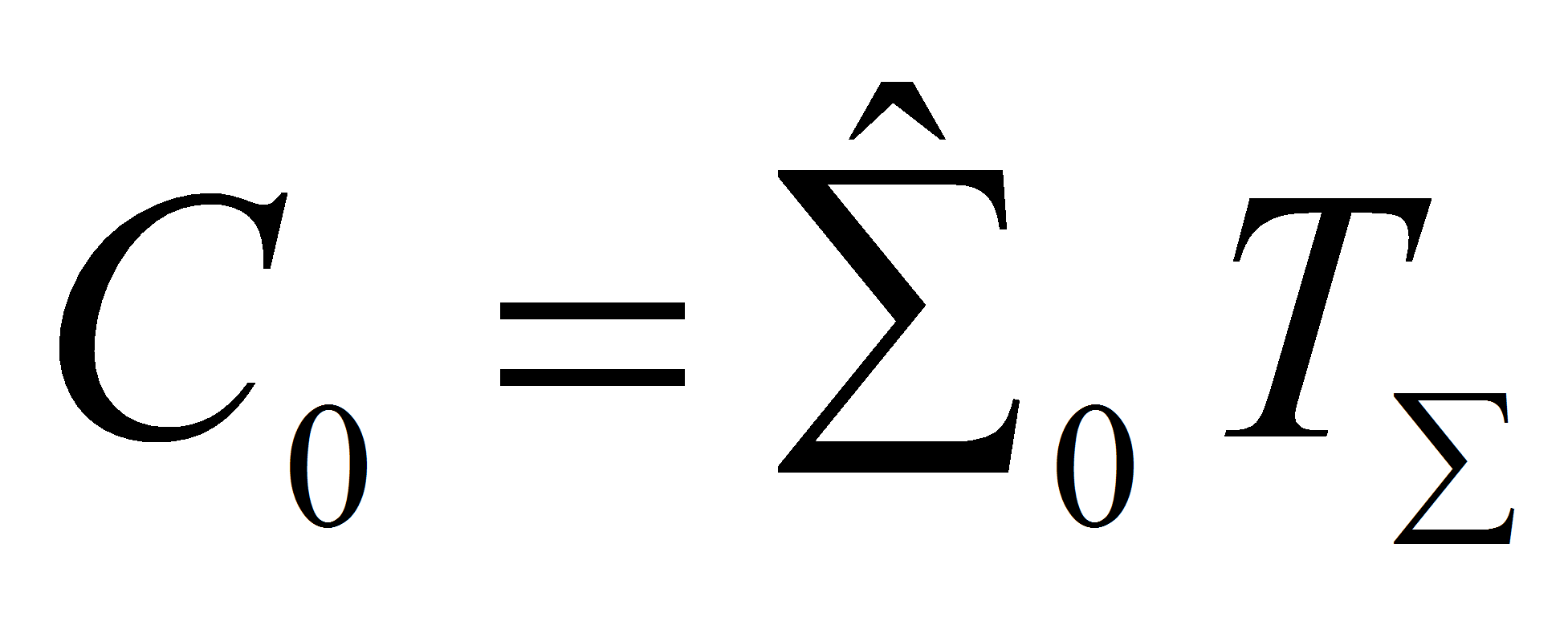 , тогда учитывая
, тогда учитывая
![]() получим
получим
Подставляя последнего формулу в первое и второе уравнение системы
(2.1) получим
![]()
Откуда делая замену
![]() после некоторых преобразований придем к системе
после некоторых преобразований придем к системе
или
где
систему (2.2) можно переписать в виде
из (2.3) видно, что исходная задача (1.12-15) свелась к исследованию операторного пучка
3. Структура спектра. Утверждение о
полноте. Сначала отметим, что так как
![]() то операторы
то операторы
![]() определяемые равенствами
определяемые равенствами
![]() положительные в
положительные в
![]() .
.
Его сужение на
![]() есть самосопряженный положительный компактный оператор, действующий в
есть самосопряженный положительный компактный оператор, действующий в
![]()
![]() Из результатов работы
Из результатов работы
![]() известно, что
известно, что
![]() ограничен и его образ
ограничен и его образ
![]() является подпространством в
является подпространством в
![]() .
Также получается, что
.
Также получается, что
![]() в
в
![]() и ограничен,
и ограничен,
Исследование операторного пучка приводит к следующему результату.
Теорема. Спектр пучка (2.4) (и задачи (1.12-15)) состоит из
собственных значений (с.з.).
![]() конечной кратности, имеющих предельные точки в
конечной кратности, имеющих предельные точки в
![]() и на
и на
![]() ,
расположен в правой полуплоскости и симметричен относительно
вещественной оси. При этом при больших
,
расположен в правой полуплоскости и симметричен относительно
вещественной оси. При этом при больших
![]() все с.з.
все с.з.
![]() ,
за исключением конечного числа точек попадают в сколь угодно малые
углы примыкающие к мнимой оси и положительной полуоси.
,
за исключением конечного числа точек попадают в сколь угодно малые
углы примыкающие к мнимой оси и положительной полуоси.
Доказательство. Введем обозначения
произвольное достаточно малое число а,
![]() выбирается достаточно большим,
выбирается достаточно большим,
![]()
![]() где
где
![]() достаточно
малое число,
достаточно
малое число,
![]() -
также достаточно мало.
-
также достаточно мало.
Прежде всего подчеркнем, что говоря о свойствах спектра пучка
![]() в этой теореме, мы рассматриваем
в этой теореме, мы рассматриваем
![]() не как пучок с абстрактными оператора перечисленными выше, а как
конкретный пучок полученный сведением именно из задачи (1.12-15). В
свете этого сразу получим, что спектр симметричен относительно
вещественной оси и
не как пучок с абстрактными оператора перечисленными выше, а как
конкретный пучок полученный сведением именно из задачи (1.12-15). В
свете этого сразу получим, что спектр симметричен относительно
вещественной оси и
![]() ,
так как это непосредственно проверяется для задачи (1.12-15).
Дискретность спектра кроме точек 0 и
,
так как это непосредственно проверяется для задачи (1.12-15).
Дискретность спектра кроме точек 0 и
![]() ,
есть следствие теоремы 5.1 из
,
есть следствие теоремы 5.1 из
![]() примененной к
примененной к
![]() .
Утверждение о локализации спектра при больших и малых
.
Утверждение о локализации спектра при больших и малых
![]() следует из аналитичности вектор – функции
следует из аналитичности вектор – функции
Функция
![]() в (2.5) является сопряженным к оператор функции
в (2.5) является сопряженным к оператор функции
![]() .
Теорема доказана.
.
Теорема доказана.
При формулировке проводимого ниже утверждения для простоты будем
считать, что все с. з.
![]() пучка
пучка
![]() (и задачи 1.12 – 15) простыми. Каждому такому
(и задачи 1.12 – 15) простыми. Каждому такому
![]() и отвечающему собственному вектору
и отвечающему собственному вектору
![]() пучка
пучка
![]() поставим в соответствие вектор
поставим в соответствие вектор
![]() из пространства
из пространства
![]() .
.
Теорема 2. Система векторов
![]() отвечающих всем с. з.
отвечающих всем с. з.
![]() при
при
![]() полна в
полна в
![]() с точностью до конечномерного подпространства.
с точностью до конечномерного подпространства.
Доказательство. Допустим, что система
![]() неполна в указанном пространстве. Тогда согласна лемме 2 из
неполна в указанном пространстве. Тогда согласна лемме 2 из
![]() найдутся векторы
найдутся векторы
![]() из которых хотя бы один отличен от нуля, такие что вектор –
функция
из которых хотя бы один отличен от нуля, такие что вектор –
функция
![]() будет аналитична в
будет аналитична в
![]() .
.
Выбираем
![]() достаточно малым, учитывая что
достаточно малым, учитывая что
![]() имеет конечный порядок роста, и применяя к ней теорему Фрагмена –
Линделефа вне области
имеет конечный порядок роста, и применяя к ней теорему Фрагмена –
Линделефа вне области
![]() можно получить, что
можно получить, что
![]() Полученное противоречие доказывает, что система
Полученное противоречие доказывает, что система
![]() полна в пространстве
полна в пространстве
![]() с точностью до конечномерного подпространства. Теорема доказана.
с точностью до конечномерного подпространства. Теорема доказана.
Замечание. Для того, чтобы сформулировать результат о полноте
с конечным дефектом для исходной задачи (1.12-15), нужно проследить
за обратным переходом от пучка
![]() из (2.4) к этой задаче.
из (2.4) к этой задаче.
Литература:
Копачевский Н. Д., Темнов А. Н. Свободные колебания вязкой стратифицированной жидкости в сосуде – Деп. в ВИНТИ 16.08.33, № 4531-83 ДЕП, 43 с.
Копачевский Н. Д., Темнов А. Н. Колебания стратифицированной жидкости в бассейне произвольной формы. – ЖВМ и МФ, 1986, т. 26, № 5.
Оразов М. Б. Некоторые вопросы спектральной теории несамосопряженных операторов и связанные с ними задачи механики. - Докт. Дисс., Ашхабад. 1983.
Ashirov A. On the problem about fluctuations of the system of a viscous stratified liquid in the elastic vessel. – The IV congress of the Turkic World mathematical society. Book of abstracts. Baku, Azerbaijan, 2011.
Краусс В. К. Внутренние волны. – Л., “Гидрометеоиздат”, 1968.
Аскеров Н. К., Крейн С. Г., Лаптев Г. И. Задача о колебаниях вязкой жидкости и связанные с ней операторные уравнения -функциональный анализ и его приложения, 1968, т. 2, № 2.
Бабский В. Г., Копачевский Н. Д., Мышкис А. Д., Слобожанин Л. А., Тюпцов А. Д. Гидромеханика невесомости. – М., “Наука”, 1976.
Гохберг И. Ц, Крейн М. Г. Введение в теорию линейных несамосопряженных операторов, М., “Наука” 1965.
Радзиевский Г. В. Квадратичный пучок операторов. – Препринт, Киев 1976.