Ключевые слова: спектральный оператор Дирака, периодический потенциал, экспоненциально убывающий, периодические функции
Рассмотрим следующий оператор Дирака
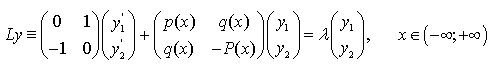(1)
где 
и 
периодическая непрерывные действительные функции, а 
комплексный параметр.
Пусть последовательности непересекающихся интервалов
являются лакунами оператора Дирака (1).
Введём решения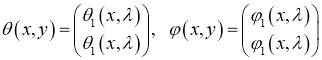 
уравнения (1)
удовлетворяющие начальным условиям:
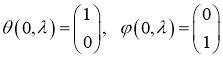
Обозначим через
, собственные значения задачи Дирихле 
для системы уравнений (1).
Справедливы следующие оценки (см.1)
, 
, 
Определение. Последовательность чисел 
и спектральные параметры 
называются спектральными данными оператора Дирака (1).
Как известно (см.2) коэффициенты оператора (1), т. е. 
периодические функции 
и 
однозначно восстанавливаются по спектральным данным.
Теорема 1. Если 
— периодический потенциал оператора Дирака (1), имеющий спектр
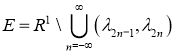и спектральные параметры , то для любого действительного параметра 
, оператор Дирака с потенциалом 
имеет тот же спектр
, и спектральные параметры 
удовлетворяют системе дифференциальных уравнений Дубровина-Трубовица
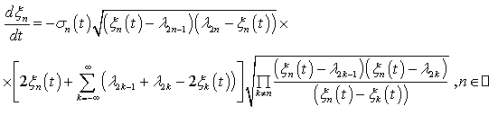(2)
а также начальным условиям
(3)
где корни понимаются в арифметическом смысле и знак 
изменяется на противоположный при каждом столкновении точки 
с границами лакуны 
.
При помощи системы уравнений Дубровина-Трубовица изучается связь длины лакун с аналитичностью коэффициентов
и оператора Дирака:
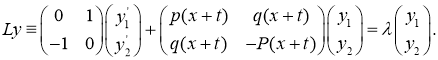
Теорема 2. Если и периодические действительные функции из класса 
и длины лакун 
экспоненциально убывают, т. е. если существуют постоянные числа 
для которых 
при любых целых 
то и является действительными аналитическими функциями на всей прямой.
Доказательство. По условию теоремы , (). Положим 
где 
.
Покажем, что при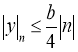 
значение 
находится в круге 
.
Действительно,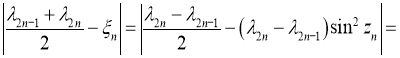 
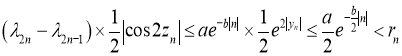
Рассмотрим множество 
комплексных последовательностей 
с действительной частью 
из пространства 
и мнимой частью 
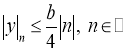
В частности при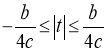 
вектор-функция 
является действительной, аналитической и формулы первого следа:
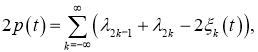
аналитична в окрестности точки 
Если вместо граничных условий 
рассмотреть граничные условия
(4)
то вышеизложенным методом можно получить аналитичность собственных значений
задачи 
и 
в точке .
Вычитая формулы второго следа
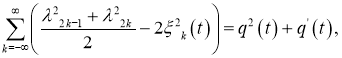
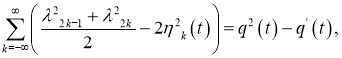друг от друга выводим аналитичность 
в точке
Рассмотрев вместо системы (1) систему:
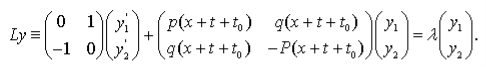
где 
действительное фиксированное число, получим аналитичность функций 
и 
в точке
Значит функции и аналитичны в точке .
Теорема 2 доказана.
Теорема 3. Если и действительные аналитические 
периодические функции, то длины лакун убывают экспоненциально.
Литература:
- Мисюра Т. В. Характеристика спектров периодической и антипериодической краевых задач, порождаемых операцией Дирака I, II. //сб. «Теория функций, функц. анализ и их приложения», Харьков, 1978,вып. 30, с. 90–101, 1979, вып. 31 стр. 102–109.
- Левитан Б. М. Обратные задачи Штурма-Лиувилля. Изв. «Наука», 1984, 289 с.
- Левитан Б. М., Саргсян И. С. Операторы Штурма-Лиувилля и Дирака. М.: Наука, 1988.
