Известно, что интерес к изучению движения жидкости в трубе с проницаемыми стенками вызван потребностью техники орошения. В результате выполнения данного исследования приводит к разработке прогрессивным способов орошения, в частности внутрипочвенного и капельного.
Для решения поставленной задачи рассмотрим движение вязкой жидкости при учете расхода через пористости стенок и гидравлического сопротивления, пропорционального первой степени расхода 
,
(1)
(2)
здесь Q — расход жидкости по сечению трубы, 
/c); S — площадь поперечного сечения трубы, 
; 
-функция, характеризующая проницаемость среды;
p,
— соответственно давление жидкости в трубе и давление внешней среды
Начальные и граничные условия для рассматриваемой задачи
При t=0 Q=0;
При x=0 (t
0) Q = Q0 = const, (3)
(l — длина трубы, (
); d — диаметр, (
)).
В случае, когда они малы, вторым членом уравнения (1) можно пренебречь. Тогда
(4)
Учитывая (2) из (4) получим уравнения для определения расхода жидкости, через трубы.
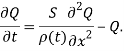(5)
В целью упрощения уравнение (5) вводим новую функцию 
(6)
Тогда
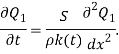(7)
С учетом начальных и граничных условий из (3)- получим:
при t=0
при x=0 (t ˃0) 
(8)
В формулу (7) вводим новую функцию по переменному 
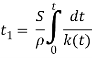(9)
Если t =0 то 
, при t
.
Выражение (9) для 
подставляем в уравнение (7). После несложным математических преобразований получим
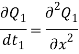(10)
Далее поставленная задача решается при следующих начальных и граничных условиях
при 
при 
(11)
где функция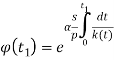 
характеризует закон распределение давлений по времени t
Решением уравнения(10) при условии (11) будет,
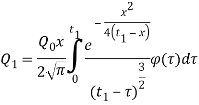(12)
Используя зависимости (6) и (9), получим формулу для расхода жидкости, протекающей через трубы
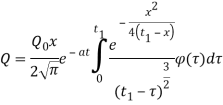(13)
Введя переменную
(14)
Из (13) получим
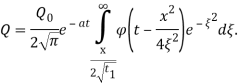(15)
При этом граничные условия принимает вид:
при 
при 
Анализ полученной формулы (15) показывает, что при 
, 
. Это означает, что фильтрация жидкости из раствора в среду через большой промежуток времени практически сводится к минимуму.
Из уравнения (2) видно, что продифференцировав функцию (15) по х один раз, можно легко получить выражения для закона изменения давления.
Представляет интерес определить, какое количество жидкости профильтровывается через пористые стенки цилиндра длиною l.
Времени через стенки профильтровавшейся жидкости равно.
Тогда общее количество жидкости, профильтровавшейся трубы за время t, равно:
(16)
Подставляя значения Q(l,t) из (15), и подставляя получим
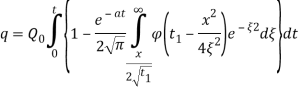(17)
При решении поставленной задачи коэффициент k(t) рассматривали как произвольную функцию, удовлетворяющую условиям (9). В конкретном случае если задана функция изменения давления, можно выбрать соответствующий закон для k(t).
Пусть скорость просачивания отверстий трубы задается в виде.
(18)
Если функция 
линейно зависит от расхода про фильтрованной жидкости за время t, получим
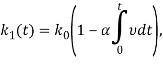(19)
То при t =0
, (20)
где 
коэффициент k(t) при t =0. Коэффициент k(t) определяется из опытов ,
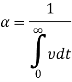
(берется из опыта).
Подставляя в (18) выражение (17), имеем.
(21)
Дифференцируя по t и обозначая 
через p1, получаем
(22)
проинтегрировав, запишем
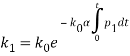(23)
В случае, когда давление р не зависит от времени,
(24)
Тогда уравнение принимает вид
(25)
Если 
постоянная величина, а 
, то окончательно получим
(26)
По формуле (17) можно определить общее количество жидкости, фильтрующейся через стенки трубы при заданных параметрах, а по (24) при известных значениях жидкости в трубе и окружающей среде — найти закон изменения k1 (t).
Предлагаемый метод вычисления расход воды в трубах с проницаемыми стенками можно применить к вопросам орошения, что даст возможность разработать гидродинамический метод расчета, обеспечивающий нормы полива сельхоз-культур, в том числе хлопчатника.
Литература:
- Д. Ф. Файзуллаев, А. И. Умаров, А. А. Шакиров «Гидродинамика одно- и двухфазных сред и её практические прилажения», 22–25стр. Ташкент, 1980
