Рассматривается задача динамической теории линейной упругости при падении сейсмической волны, перпендикулярной к оси длинной трубы, уложенной в высокой насыпи и заполненной идеальной сжимаемой жидкостью.
Let's consider a task of the dynamic theory of linear elasticity at fall of a seismic wave perpendicularly to an axis of the long pipe stacked in high and a filled ideal compressed liquid.
Рассмотрим задачу динамической теории линейной упругости при падении сейсмической волны перпендикулярно к оси длинной трубы, уложенной в высокой насыпи и заполненной идеальной сжимаемой жидкостью. Расчетная схема представлена на рис.1. Известное из динамической теории упругости уравнение движения в векторной форме для изотропного тела имеет вид: ![]()
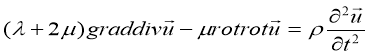 ,(1)
,(1)
где – плотность среды, а все остальные обозначения имеют тот же смысл, что и в уравнении статической теории упругости [1]. Произведем стандартное преобразование уравнения следующим образом. Представим вектор перемещений в виде:
![]() (2)
(2)
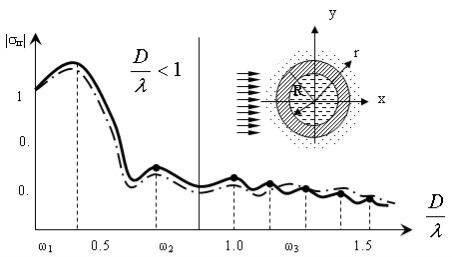
Рис. 1. Зависимость напряжения от волновых чисел
Подставив (2) в (1) и учитывая, что движение частицы имеет установившийся характер, а также пренебрегая массовыми силами, =0 т. к. в соответствии с принципом суперпозиции их можно учесть отдельно при решении статической задачи, получим в случае плоской деформации следующую систему волновых уравнений Гельмгольца для потенциалов:
![]() ,(3)
,(3)
где и волновые числа 2=2/(+2), 2=2/.
В полярной системе координат уравнение Гельмгольца запишется в виде:
Vrr+r-1Vr+r-2V+k2V=0, V=(,Ψ); k=;.(4)
Решение уравнения (4) ищется в виде ряда:
![]() .(5)
.(5)
Подставив (5) в (4) и приравняв коэффициенты при соответствующих гармониках, получим обыкновенное дифференциальное уравнение Бесселя
r-2V»n+r-1V'n+(k2r2-n2)Vn=0, которое имеет частное решение в виде цилиндрической функции Zn(kr). Тогда окончательное решение системы (1) запишется в виде:
![]() (6)
(6)
Решения уравнение (4) при r→ удовлетворяет условия излучения Зоммерфельда [1]. Для решения поставленной задачи ставится граничных условия жесткого контакта при r=R и r=R0. Учитывая полученные соотношения, выведем решение краевой задачи для случая падения на подземную трубу волны сжатия. Волновой потенциал такой волны имеет вид
![]() , где
, где ![]() , In – цилиндрическая функция Бесселя первого рода [1]. Потенциалы волн, отраженных от трубы в грунт, дальше имеют вид (6) и в то же время удовлетворяют условиям излучения, поэтому согласно [1] записываются в виде:
, In – цилиндрическая функция Бесселя первого рода [1]. Потенциалы волн, отраженных от трубы в грунт, дальше имеют вид (6) и в то же время удовлетворяют условиям излучения, поэтому согласно [1] записываются в виде:
![]()
где Hn(1) — цилиндрическая функция Ханкеля первого рода [1]. Суммарные потенциалы в грунте равны: 1=1(i)+ 1(r); 1=1(r).
Потенциал скоростей в сжимаемой жидкости имеет вид:
![]() .
.
Компоненты с индексом «3» (жидкость) получены согласно [1,2] с помощью линеаризованного интеграла Коши-Лагранжа для гидродинамического давления идеальной жидкости. Неизвестные коэффициенты An, Bn, Cn, Dn, En, Fn, Gn определяются из системы линейных уравнений седьмого порядка. Кроме того, в случае отсутствия жидкости в трубе: σrr=0. На рис.2 проведена изменение радиальных напряжений в зависимости от безразмерной волновых чисел при различных соотношениях параметров
η1= ![]() = 0,4; ν=0,25; E =
= 0,4; ν=0,25; E = ![]() = 0,5, 2 =
= 0,5, 2 = ![]() . Из анализов полученных результатов выявлено, что в области коротких волн распределение напряжение в трубе с жидкостью отличается до 40 % (рис.1). Расчеты показывает, что при фиксированных значениях амплитуды и длительности действия падающей волны с увеличением акустических параметров жидкости, прогибы и усилия также увеличиваются. Увеличение жесткости тоннеля или ее толщины приводит к снижению прогибов и к увлечению усилий. Причем с увеличением толщины усилия растут быстрее, чем изгибающие моменты, а изгибающие моменты быстрее, чем поперечные силы.
. Из анализов полученных результатов выявлено, что в области коротких волн распределение напряжение в трубе с жидкостью отличается до 40 % (рис.1). Расчеты показывает, что при фиксированных значениях амплитуды и длительности действия падающей волны с увеличением акустических параметров жидкости, прогибы и усилия также увеличиваются. Увеличение жесткости тоннеля или ее толщины приводит к снижению прогибов и к увлечению усилий. Причем с увеличением толщины усилия растут быстрее, чем изгибающие моменты, а изгибающие моменты быстрее, чем поперечные силы.
Литература:
- Сафаров И. И. Колебания и волны в диссипативно неоднородных средах и конструкциях. // Ташкент: Фан, 1992. – C. 250.
- Рашидов Т. Р. Динамическая теория сейсмостойкости сложных систем подземных сооружений. Изд. «Фан», Ташкент. 1973 й, 180 с.
- Жарий О. Ю., Улитко А. Ф. Введение в механику нестационарных колебаний и волн. — Киев: Высшая школа Головное изд-во, 1989. – 184 с.







