Расчет напряженно-деформированного состояния цилиндрической оболочки по заданным перемещениям



Расчет напряженно-деформированного состояния цилиндрической оболочки по заданным перемещениям

Кабриц Сергей Александрович, кандидат физико-математических наук, доцент;

Еременко Владимир Романович, студент;

Ма-ю-шан Владислав Витальевич, студент

Санкт-Петербургский государственный университет

Ложкин Егор Николаевич, начальник технического отдела

ООО «ЭНТЭ» (г. Санкт-Петербург)

Рассматривается модельная задача о НДС (напряженно-деформированное состояние) цилиндрической оболочки при вертикальной нагрузке, возникающей при заданных жестких смещениях ряда поперечных сечений цилиндра. Подобная задача возникает при проверке состояния газопровода по измеренным перемещениям в некоторых сечениях трубы. На основе линейной теории оболочек исследуется НДС от действия различных вариантов нагрузок, обеспечивающих одни и те же заданные перемещения. Соответствующие линейные одномерные краевые задачи решаются численно. Как известно, в подобных задачах присутствует значительный краевой эффект, поэтому для решения используется метод ортогональной прогонки Годунова, который обеспечивает получение численного решения с приемлемой точностью.

Ключевые слова: цилиндрическая оболочка, деформация, напряжение, перемещение, ортогональная прогонка.

Роль трубопроводного транспорта в системе нефтегазовой отрасли очень высока, поскольку он является одним из недорогих видов транспортировки нефти. Помимо энергетического обеспечения страны, трубопроводы позволяют уменьшить нагрузку на железнодорожный транспорт.

Магистральные трубопроводы состоят из нескольких основных элементов, функционирование каждого из которых необходимо для продолжения транспортировки. Однако анализ надежности и систематизация произошедших аварий показывают, что наибольшее влияние на надежность конструкции оказывают её прямолинейные участки. В связи с этим, важным становится повышение надежности линейной части на всех этапах создания трубопровода. Также важно адекватно оценить влияние внешних нагрузок на конструкции, то есть необходимо исследовать конструкцию на надежность при помощи анализа НДС трубопровода.

Расчет НДС предполагает знание всех нагрузок, действующих на трубопровод. Эти нагрузки меняются в процессе многолетней эксплуатации трубопровода. Причинами изменения нагрузок являются подвижки грунта, коррозионные повреждения трубопровода [10] и т. п. Одним из способов контроля деформации трубопровода является периодическая геодезическая съемка, которая позволяет определить смещения контрольных точек по сравнению с предыдущим положением.

Необходимо определить изменение НДС фрагмента трубопровода по вертикальным смещениям, полученным посредством геодезической съемки. Тонкостенность рассматриваемого объекта позволяет в качестве математической модели использовать линейную теорию тонких цилиндрических оболочек [9,13].

Проблемам нелинейного деформирования оболочек посвящена работа [5]. Разработанные методы решения краевых задач для систем нелинейных дифференциальных уравнений можно использовать и при решении различных задач в технике, биологии, медицине, экономике и других областях [1,3,4,8,11,12].

Система уравнений для определения НДС цилиндрической оболочки

Обычно решение задач для цилиндрических оболочек ищут в виде тригонометрических рядов по круговой координате [7,9].

(1)

Для определения коэффициентов рядов (1) при k=1 используется система дифференциальных уравнений следующего вида [6,7]:

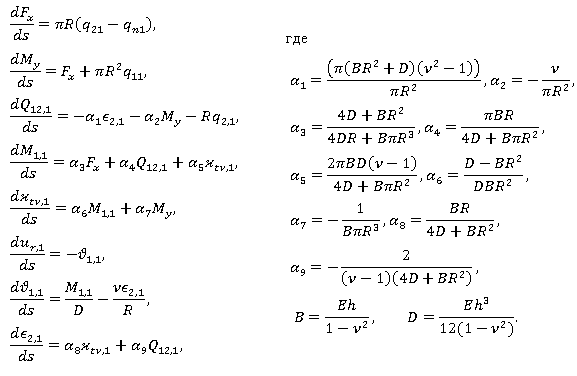(2)

E — модуль Юнга, ν — коэффициент Пуассона, h — толщина оболочки, D — цилиндрическая жесткость, B — жесткость на растяжение.

Формулирование краевой задачи

Введем обозначения , где

Систему дифференциальных уравнений (2) можно представить в виде:

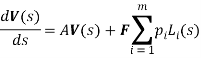(3)

с граничными условиями

(4)

— прямоугольные матрицы следующего вида

в данном случае постоянной толщины, A — постоянная матрица

В (3) функция — меняется в зависимости, от способа приложения силы.

Для случая сосредоточенной нагрузки

При использовании интерполяционного полинома Лагранжа

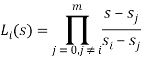
Требуется проинтегрировать систему (3) с граничными условиями (4). Для решения поставленной задачи используется численный метод ортогональной прогонки Годунова [2].

Алгоритм расчета нагрузок по заданным перемещениям

При единичных нагрузках , решается система (3) с граничными условиями (4). На каждом i-ом шаге получается вектор перемещений с компонентами

— кордината, в которой известно перемещение(). Из векторов-строк формируется матрица податливости .

Вектор заданных смещений u и матрица податливости Q позволяют найти значения параметров нагружения . Для этого необходимо решить систему линейных алгебраических уравнений: . Полученные используются при решении системы (3).

Расчет проводился для прямолинейного участка трубопровода длины . Величины с тильдой — записаны в безразмерном виде. Вертикальные перемещения поперечного сечения трубопровода были измерены в трех точках

(5)

- перемещение трубопровода в точке . Эти точки отмечены на графике перемещений вдоль трубопровода, рис. 1, цифрами 1, 2 и 3 соответственно.

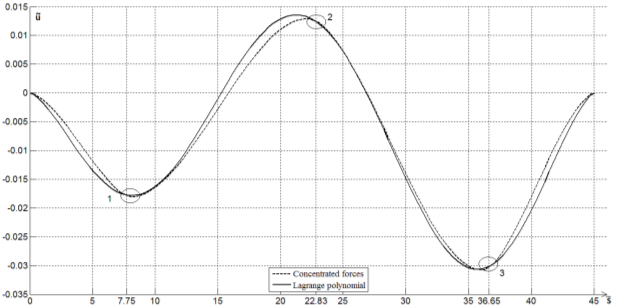Рис. 1. График полученных перемещений

Значения нагрузок, которые обеспечивают перемещения (5):

а) в случае сосредоточенных нагрузок :

б) в случае интерполяции полиномом Лагранжа :

Используя полученные p, находим НДС трубопровода в двух случаях нагружения.

Программа тестировалась на задаче, рассмотренной в работе [7] (случай сосредоточенных нагрузок (А)) результаты совпали.

Усилия T и моменты M определяются по следующим формулам

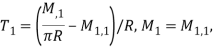
Безразмерные тангенциальные и максимальные изгибные напряжения определяются по формулам:

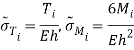
Анализ полученных результатов

Для того чтобы оценить напряжение по сравнению с максимально допустимым, необходимо построить грфики напряжений на внешней и внутренней поверхностях трубопровода, для всех случаев нагружения. Так же построим на графике предельные значения напряжений для данного материала обозначим их пунктирными линиями.

Модуль юнга E = 206000 МПа, максимально допустимое напряжение = 563 МПа, безразмерная величина максимально допустимого напряжения:

Формулы для рассчета осевых безразмерных напряжений.

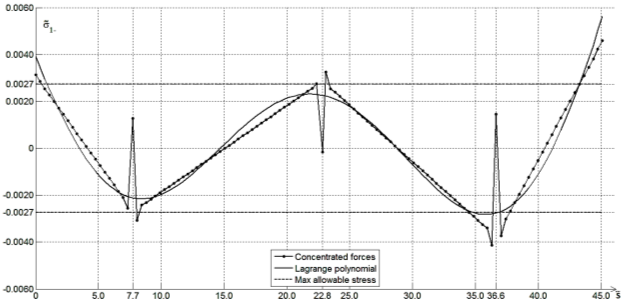
Рис. 2. График осевых напряжений на внутренней поверхности трубы

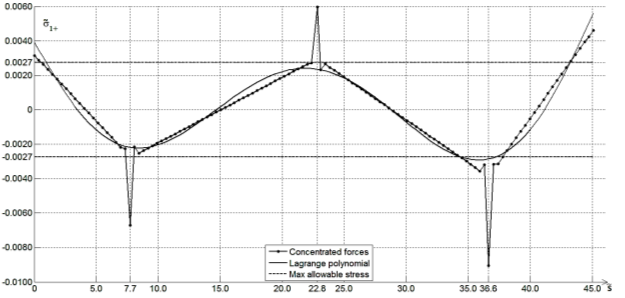
Рис. 3. График осевых напряжений на внешней поверхности трубы

Из графиков 2, 3 видно, что в зависимости от способа нагружения получаются разные результаты. Так график напряжений от действия сосредоточенных нагрузок, выходит за пределы максимально допустимого напряжения во всех местах приложения силы. График от действия распределенных, полиномом Лагранжа, нагрузок, ведет себя гораздо лучше, оставаясь в пределах допустимого. Только в точке с координатой 36.65 видны выходы за пределы максимально допустимого напряжения в обоих случаях нагружения, здесь возможно повреждение трубопровода.

Формулы для рассчета окружных безразмерных напряжений

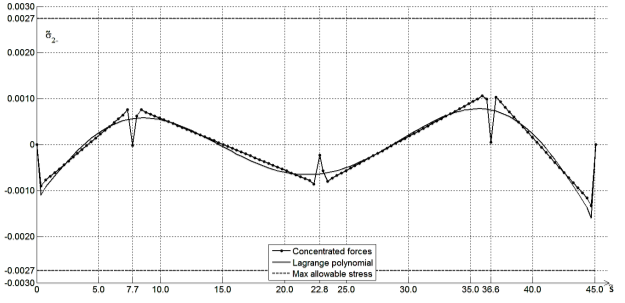
Рис. 4. График окружных напряжений на внутренней поверхности трубы

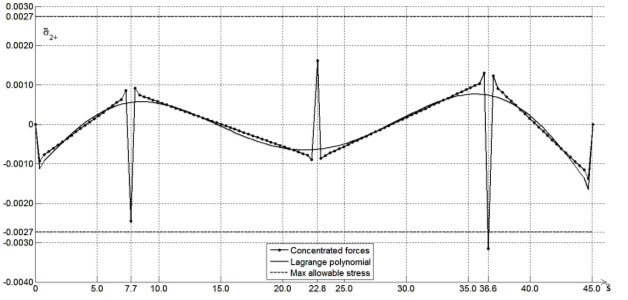
Рис. 5. График окружных напряжений на внешней поверхности трубы

На графиках, рис. 4,5 видно, что значения окружных напряжений меньше меридиональных и не выходят за пределы максимально допустимых, кроме случая сосредоточенных нагрузок в точке с координатой 36.65 на внешней поверхности трубы.

Заключение

Разработана методика расчета изменения НДС фрагмента трубопровода по измеренным вертикальным смещениям в некоторых точках. Построен алгоритм определения параметров нагружения, обеспечивающих измеренные перемещения во фрагменте трубопровода. Определено НДС для двух способов нагружения «жесткого» (сосредоточенные нагрузки в точках снятия перемещений) и «мягкого» (непрерывно распределенная нагрузка).

Литература:

1. Гасратова Н. А., Бойцов Д. С., Габриелян Л. А., Тюганова Т. М. Математическая модель иммунного ответа организма млекопитающих на поражение кожи ожогом // Молодой ученый. 2014. № 12. С. 1–7.
2. Годунов С. К. Метод ортогональной прогонки для решения систем разностных уравнений // Журнал Вычислительной математики и математической физики, 1962. Т. 2. № 6. С. 972–982.
3. Горыня Е. В., Колпак Е. П. Математические модели поиска экологической ниши. В сборнике: Устойчивость и процессы управления Материалы III международной конференции. 2015. С. 469–470.
4. Dal' Yu.M., Pronina Yu.G. On concentrated forces and moments in an elastic half-plane. Вестник Санкт-Петербургского университета. Серия 1. Математика. Механика. Астрономия. 1998. № 1. С. 57–60.
5. Кабриц С. А., Мальков В. М., Мансурова С. Е. Нелинейные уравнения плоского слоя для трех моделей эластомерного материала Известия Российской академии наук. Механика твердого тела. 2001. № 1. С. 38.
6. Кабриц С. А., Шамина В. А. Изгиб оболочки вращения поперечной силой и моментом // Вестник. СПБГУ, 2014. С. 261–269.
7. Kabrits S. A., Shamina V. A. Cilindrical shell under the action of the ring load // Seventh Polyakhov’s Reading, 2015 International conference on Mechanics, 2015. — P. 1–3.
8. Колпак Е. П., Горыня Е. В., Селицкая Е. А. О моделях А. Д. Базыкина «хищник — жертва». Молодой ученый. 2016. № 2 (106). С. 12–20.
9. Новожилов В. В. Теория тонких оболочек. Л.: Судопромгиз, 1962. 432 с.
10. Пронина Ю. Г. Оценка устойчивости упругой трубы под давлением коррозионных сред. Вестник Санкт-Петербургского университета. Серия 10. Прикладная математика. Информатика. Процессы управления. 2006. № 3. С. 55–63.
11. Pronina Y. G. Study of possible void nucleation and growth in solids in the framefork of the Davis-Nadai deformation theory. Mechanics of Solids. 2014. Т. 49. № 3. С. 302–313.
12. Pronina Y. G. Analytical solution for decelerated mechanochemical corrosion of pressurized elastic-perfectly plastic thick-walled spheres. Corrosion Science. 2015. Т. 90. С. 161–167.
13. Черных К. Ф. Линейная теория оболочек. Ч.1,2. Л.: Изд-во Ленинградского Университета. Ч.1, 1962. 272с. Ч.2, 1964. 395 с.